探空仪湿敏电容器的误差校正模型研究*

张颖超，王飞帆，廖俊玲

（南京信息工程大学信息与控制学院，江苏南京 210044）

0 引言

探空仪测量的高空大气湿度是大气探测综合观测系统中的关键要素之一，其可靠与否直接影响着天气预报和气候预测的准确性。目前，以芬兰VAISALA公司为代表的全球各大电子探空仪生产商均采用了精度更高和具有长期稳定性的湿敏电容器作为感湿元件［1，2］。但是，湿敏电容器的介电常数会随温度的改变而变化，特别是，当探空仪处于高空低温环境时，会有严重的温度漂移和零点漂移现象，加上受外围电路的影响产生的非线性关系，湿度传感器的测量精度会明显降低，测量结果会存在较大的误差。因此，需要建立误差校正网络对传感器的输出进行温度补偿和非线性校正［3，4］。

神经网络可以作为万能逼近器，拟合任意非线性函数。BP神经网络是目前使用最广泛的神经网络模型，常被用于传感器的误差校正，但也有网络层数和神经元个数难于确定、训练时间长以及容易陷入局部极小值等缺点。本文设计了基于T-S模糊系统的混合型pi-sigma模糊神经网络拟合模型，采用魏海坤教授给出的K-means聚类算法对10个二维模糊子集的隶属函数进行预处理［5］，利用张雨农教授提出的权值直接确定方法选择模糊规则结论多项式的系数［6］，从而有效提高了网络训练速度和网络结构的稳定性。经实验证明:pi-sigma模糊神经网络在低温段的预测精度优于BP神经网络。

1 模糊神经网络

1．1 混合型pi-sigma模糊神经网络

pi-sigma神经网络是一种既含有求和节点，又含有乘积节点的网络模型，它与T-S模糊系统有机结合形成了一种混合型pi-sigma模糊神经网络，该网络可以方便地在线修正隶属函数和参数［7，8］。

图1所示为本文构建的用于湿度传感器误差校正的双输入单输出含有10个模糊神经元（即模糊规则）的网络结构，在该网络中，∑和∏分别表示相加和相乘运算。不失一般性，网络的输出为

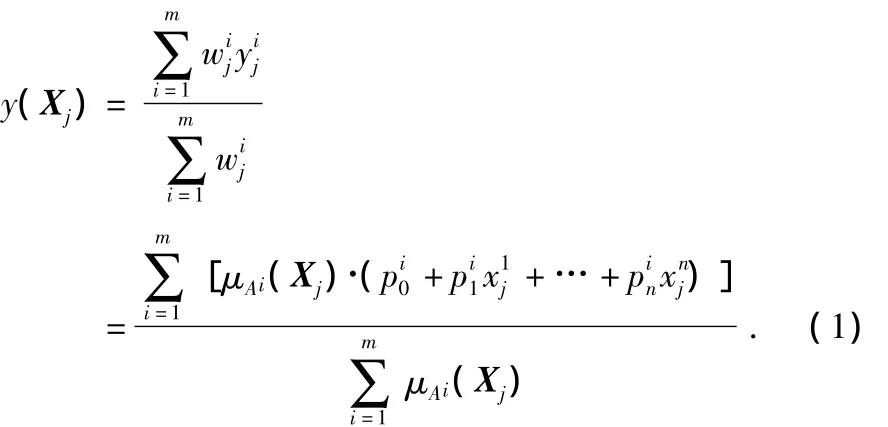
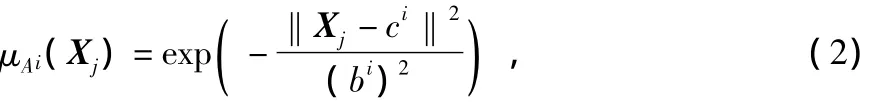
式中 ci为隶属函数节点的n维中心矢量;‖Xj－ci‖为输入矢量到节点中心的欧氏距离;bi为隶属函数节点的基宽度参数。

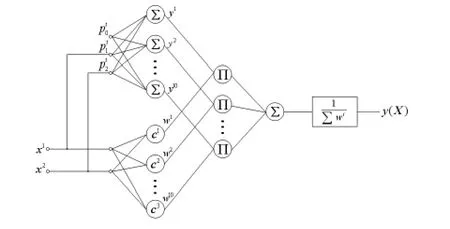
图1 pi-sigma模糊神经网络结构Fig 1 Structure of pi-sigma fuzzy neural network

1．2 K-means聚类方法

K-means聚类算法的思路是对样本输入进行无监督学习，确定各网络节点的数据中心ci，然后根据各数据中心之间的距离确定各节点的基宽度参数bi［9］。

设X1，X2，…XN为N个n维样本输入，k为迭代次数，第k次迭代时的聚类中心为c1（k），c2（k），…，ci（k），相应的聚类域为w1（k），w2（k），…，wi（k）。

K-means聚类算法确定ci和bi的步骤如下:

1）算法初始化:选择前m个样本输入作为初始聚类中心。

2）计算所有样本输入与聚类中心的欧氏距离‖Xjci（k）‖，j=1，2，…，N。

3）对样本输入Xj，按最小距离原则对其进行分类:

4）重新计算各类新的聚类中心

式中Ni为第i个聚类域wi（k）中包含的样本数。

5）如果ci（k+1）≠ci（k），转到步骤（2）;否则，聚类结束，继续步骤（3）。

6）根据各聚类中心之间的距离确定各节点的基宽度参数bi。取bi=κdi，其中di为第i个数据中心与离他最近的数据中心之间的距离，即

其中，h=1，2，…，m，κ 称重叠系数。

可见，通过K-means聚类根据各中心矢量间的距离即可直接确定各模糊神经元的基宽度参数，减轻了网络训练的负荷。

1．3 权值直接确定法

根据非齐次方程组的求解方法和BP算法权值迭代公式可得，网络最优稳态权值的求解可以转化为求矩阵方程最小二乘最优解的过程［10］。

设 A∈Rq×n，W∈Rn×m，G∈Rq×m，则 W=A+G 是相容矩阵方程AW=G的唯一极小范数解，或是矛盾方程AW=G的唯一极小范数最小二乘解。A+=（ATA）－1AT称为A的伪逆，G为目标输出矩阵。

针对图1所示的网络结构有

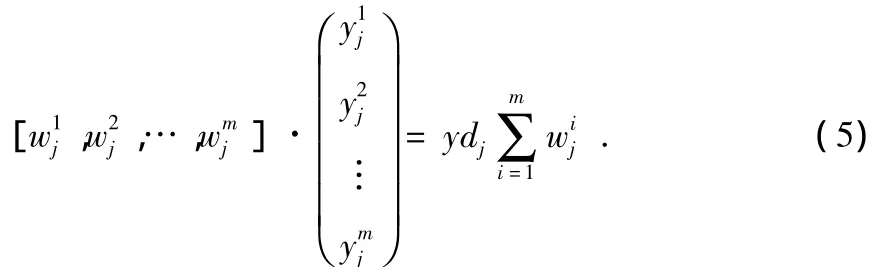
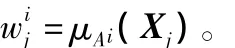
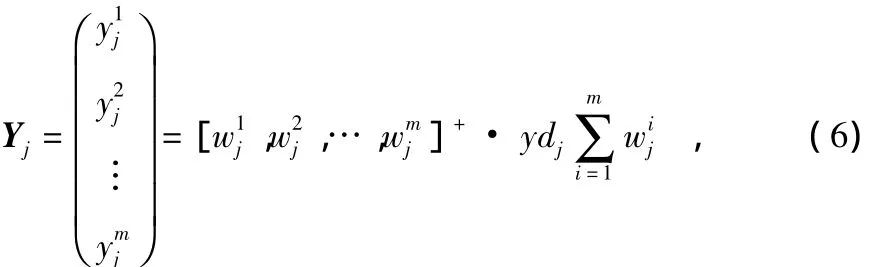
从而求得模糊规则结论矩阵

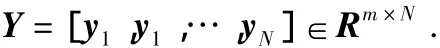
对给定的训练样本

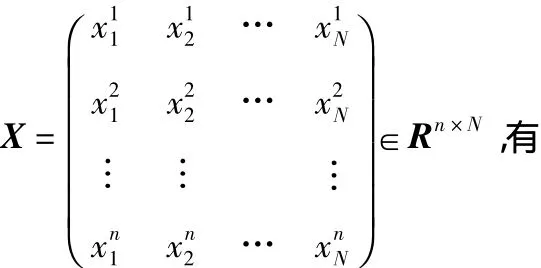
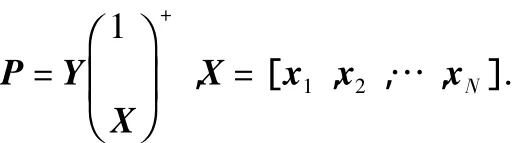
利用权值直接确定法避免了BP算法的迭代过程，极大地提高了网络的训练速度。

2 模糊神经网络的实验测试与结果分析

对配备新型HUMICAP@180湿敏电容的HMP45D温湿集成传感器进行实验测量。实验环境采用L—DP2双温双压法精密湿度发生器，设定温度范围为－30～40℃，湿度范围为10%～95%RH。温度每隔10℃、湿度每隔5%RH进行一次测量，得到144个测量值作为训练样本，其测量误差如图2所示。

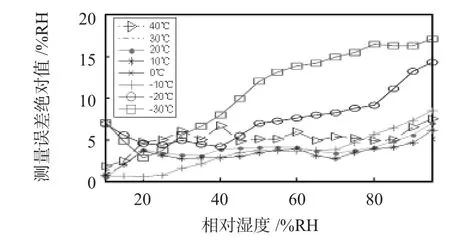
图2 训练样本各温度下的测量误差Fig 2 Measurement error of train sample at different temperature

可以看出:传感器越接近低温高湿区测量误差越明显，在0℃以上测量误差基本处于8%RH以内，但仍然普遍存在非线性关系，因此，必须对其进行误差校正。

利用Matlab的mapminmax函数对样本输入归一化，并对其进行乱序重排，分别代入BP神经网络和pi-sigma模糊神经网络进行训练，进而建立传感器误差校正模型。BP神经网络选用2—9—6—1的三层结构，隐层和输出层传输函数分别为双曲正切和线性函数，训练函数为trainlm，利用Matlab神经网络工具箱建立和训练网络。pi-sigma模糊神经网络依据前文所述，通过Matlab编程实现。

定义湿度相对误差为

比较两者经过训练的拟合输出的相对误差如图3，训练时间如表1。

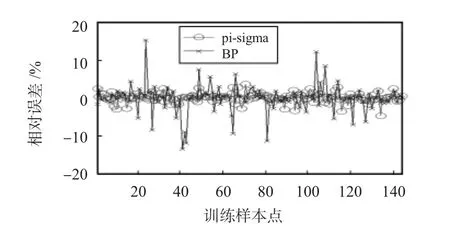
图3 训练样本拟合结果相对误差Fig 3 Relative error of train sample fitting result

pi-sigma模糊神经网络和BP神经网络最大相对误差分别为4．774%和15．27%，可以看出:pi-sigma模糊神经网络的相对误差都比较接近0，大部分小于3%，相比BP神经网络拟合精度更高，能够满足气象观测要求的指标［2］。

表1 训练时间Tab 1 Training time

图3和表1说明:同BP神经网络相比，使用K-means聚类和权值直接确定法不仅保证了pi-sigma模糊神经网络的准确性，而且缩短了网络的训练时间。

为了检验和比较2种模型的泛化能力，测试中选取了4组温湿度均不与训练样本设定值相重合的检验样本。图4给出了其中一组样本的拟合结果对比。

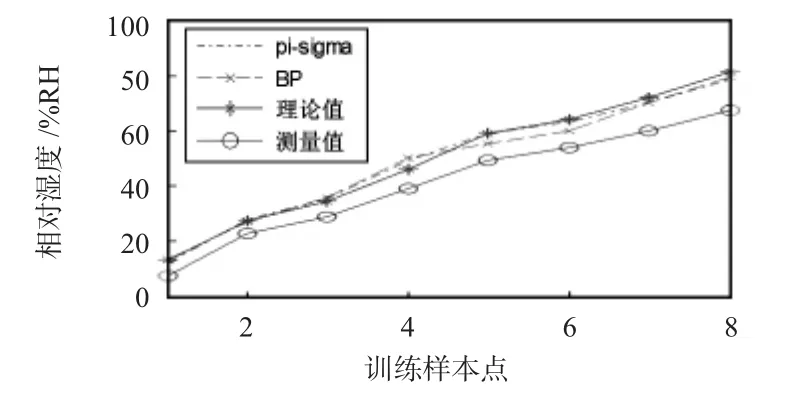
图4 检验样本误差对比Fig 4 Error contrast of inspection sample

从图4可以看出:未经补偿的实验数据和理论值有很大偏差，而经过网络校正后的预测结果基本接近理论值，其中pi-sigma模糊神经网络和理论值的曲线重合度比BP神经网络更高，由于检测样本的温度和湿度是完全独立于训练样本的，因此，证明了误差校正模型拥有很好的泛化能力。

定义均方误差为

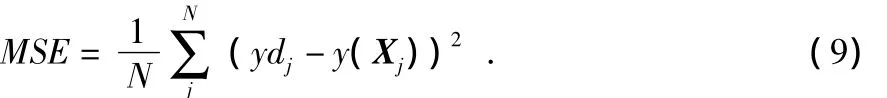
4组检验样本的误差结果如表2。

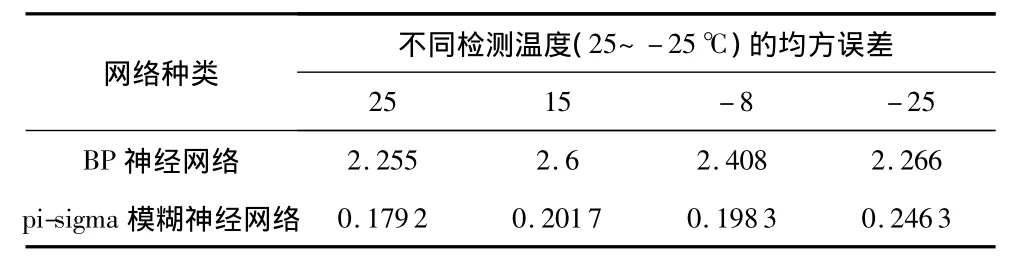
表2 检测样本均方误差Tab 2 Mean square error of test sample

该表显示:pi-sigma模糊神经网络的预测结果均方误差基本都在0．2左右，而BP神经网络的预测结果均方误差都在2以上，证明了pi-sigma模糊神经网路的泛化能力要优于BP神经网络。

3 结束语

本文设计了一种基于T-S模糊模型的混合型pi-sigma模糊神经网络实现对探空仪湿敏电容传感器的温度补偿和非线性校正。通过采用K-means聚类算法和权值直接确定方法直接确定了模糊神经元的模糊规则和模糊规则结论多项式系数的初值，节省了训练时间，提高了收敛速度，有效避免了训练过程落入局部极值。通过与BP神经网络的实验对比表明:本文构建模糊神经网络的拥有更高的拟合精度、更强的泛化能力和更快的训练速度。

［1］ Kouda S，Dibi Z，Meddour F．Modeling of a smart humidity sensor［C］∥ International Conference on Microelectronics，2008:135－138．

［2］ 徐文静．GTS探空仪碳湿敏元件性能测试数据分析及相对湿度订正［J］．气象科技，2007，35（3）:423 －428．

［3］ 侯立群，张志娟，仝卫国．基于RBF神经网络的传感器非线性误差校正方法［J］．传感器技术，2004，23（3）:43 －45．

［4］ 唐 炜，徐晓苏．基于温度补偿的传感器建模方法及其应用［J］．计量技术，2007（2）:64－68．

［5］ 魏海坤．神经网络结构设计的理论与方法［M］．北京:国防工业出版社，2005．

［6］ 张雨浓，杨逸文，李 巍．神经网络权值直接确定法［M］．广州:中山大学出版社，2010．

［7］ 刘金锟．智能控制［M］．2版．北京:电子工业出版社，2009．

［8］ 潘玉民，赵立永，张全柱．瓦斯涌出量的混合pi-sigma模糊神经网络预测模型［J］．计算机应用，2012，32（4）:1045 －1049．

［9］ Tzortzis G F，Likas A C．The global kernel k-means algorithm for clustering in feature space［J］．IEEE Transactions on Neural Networks，2009，20（7）:1181 －1194．

［10］张雨浓．SIMO傅里叶三角基神经网络的权值直接确定法和结构自确定算法［J］．信息与控制，2011，40（4）:507 －513．