脉冲涡流矩形传感器参数的仿真优化与实验*
2013-10-22周德强闫向阳尤丽华张秋菊
周德强,闫向阳,尤丽华,张秋菊
(1.江南大学机械工程学院,江苏无锡 214122;2.无锡国盛精密模具有限公司,江苏无锡 214024)
0 引言
脉冲涡流无损检测方法是目前涡流检测领域的一个研究热点,激励脉冲包含的频谱宽,可提取的缺陷信息丰富[1],对深层缺陷检测能力强,应用前景广阔。传统的圆柱形脉冲涡流传感器可以对表面和近表面缺陷进行定量检测[2],但激励磁场直接穿过检测线圈,使得激励信号对检测信号产生很大的干扰。文献[3]指出,在矩形载流线圈激励下,感应电磁场在金属铝板中的衰减率较传统的涡流激励线圈要小,矩形载流线圈激励的涡流渗透深度更深。此外,脉冲激励矩形线圈具有如下优点[4~7]:在裂纹检测中由于提离效应影响小而对微小裂纹具有高灵敏度;能有效消除边缘效应的影响;由于具有方向特性,矩形探头能够产生均匀的涡流分布等。我国学者何赟泽等人也对脉冲涡流矩形传感器开展了大量研究,提出了蝶形图新型特征量等对缺陷进行定量与分类识别[8~10]。因此,开展脉冲涡流矩形传感器的优化设计十分必要。
脉冲涡流矩形传感器可采用2种方式进行检测:脉冲涡流矩形传感器平行与垂直被检测对象。本文以脉冲涡流矩形传感器平行于被检测对象为模型,采用Comsol Multiphysics有限元仿真软件建立了脉冲涡流矩形传感器检测模型,通过电导率的改变,提取磁场的瞬态信号。通过改变矩形传感器的尺寸参数即改变长、宽、高的比值,分析传感器尺寸参数的变化对传感器灵敏度和线性度的影响。然后根据仿真结果,设计制作了3种尺寸的矩形探头,并使用这些探头对铝板的表面缺陷进行了检测,通过对比仿真和实验的结果,得出了矩形传感器的最佳尺寸参数。
1 仿真模型的建立和参数设置
1.1 仿真模型的建立
本文采用Comsol Multiphysics建立了脉冲涡流矩形探头传感器三维模型。在AC/DC模块下选择物理场为磁场,并且在瞬态求解下进行仿真分析。整体建模结构如图1所示。
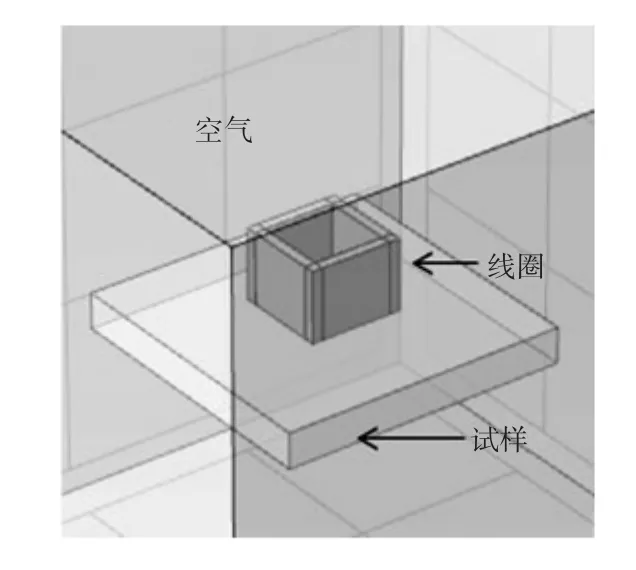
图1 脉冲涡流矩形探头有限元仿真模型图Fig 1 Finite element simulation model of pulsed eddy current rectangular probe
1.2 电流设定与其他参数说明
图2为线圈的俯视图。激励电流密度大小定义变量为curd,curd=N×0.5 ×sgnt/A,N=T×H/d2。其中,N为线圈的匝数,0.5为设定的电流大小,t为时间,A为线圈的横截面积,T表示线圈的厚度,实验设定为3 mm,H为线圈的高度,d为漆包线直径,拟定为0.3 mm。按照逆时针方向设定电流密度方向,磁场方向z轴为正向。按照图示①~⑧的顺序为各个线圈添加外部电流密度,此模型的电流只需要添加x,y2个方向,z方向始终为0。如模块1,只在x方向有电流,故x方向外部电流密度设为curdA/m2,y方向为0;模块4其电流方向为135°角,则x方向外部电流密度为-curd/sqrt(2)A/m2,y方向为curd/sqrt(2)A/m2,依次完成对矩形线圈的电流设定。
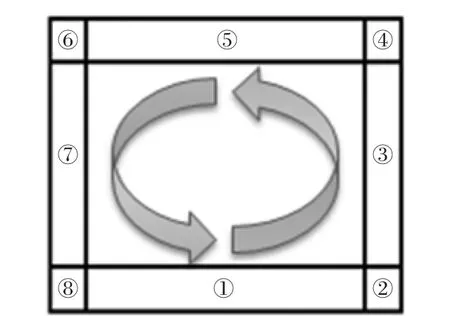
图2 矩形线圈的俯视图Fig 2 Top view of the rectangular coil
被测试样为铝板,其尺寸(长×宽×高)为100 mm×100 mm×10 mm,相对磁导率为1,电导率为 σ=3.774×107S/m。激励电流幅值大小为0.5 A,频率为100 Hz。传感器放置在试样上方0.5 mm处,即提离高度为0.5 mm。
2 仿真实验与结果分析
本文采用单因素轮换法进行仿真实验,即控制矩形线圈的2个变量不变,改变另外一个变量来探究传感器的灵敏度。首次实验保持长宽相等,改变高度来仿真,即按比例变化为1∶1∶h,h表示变化的高度,取值从1变化到2,每次递增0.25。比例基值为20 mm,线圈厚度为3 mm。仿真安排如表1所示。
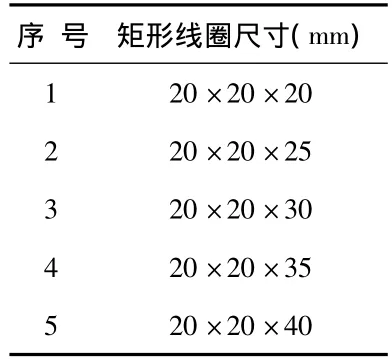
表1 高度变化的激励线圈尺寸参数表Tab 1 Excitation coil size parameters of height change
每次仿真求取0.005 s内500个点的磁场变化情况,提取试样上方0.5 mm处的磁通密度z轴分量作为研究对象。电导率没有变化时的数据,称之为参考信号,电导率逐次增加10%求取信号。采用各个电导率变化仿真得到的信号减去参考信号得到差分信号。差分信号有明显的峰值信息,可以有效地提高传感器的灵敏度。如图3所示,①为参考信号,即电导率没有变化的信号;②为电导率变化50%的信号;③为参考信号减去电导率变化信号得到的差分信号。
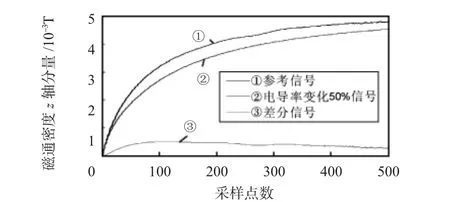
图3 参考信号与差分信号等关系图Fig 3 Reference signal and differential signal etc
图4为提取不同电导率变化的差分信号峰值,该曲线反应的是当长、宽、高比值为1∶1∶2的时差分信号结果。其斜率反映矩形线圈传感器的灵敏度与线性度。通过对比不同尺寸参数下的差分信号峰值特征,得出不同尺寸传感器的优劣,进而优化选择出最佳的尺寸参数。
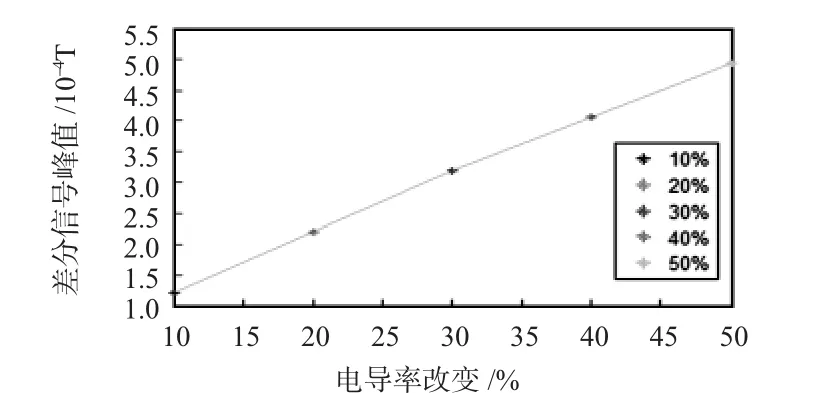
图4 差分信号峰值随电导率变化Fig 4 Differential signal peak value vs conductivity changes
图5为长宽比例不变,高度变化的综合图。通过对比可知在长、宽、高比例为1∶1∶1.5时灵敏度最高,线性度也最好,即为最优比值。
同理对长和宽的变化实施第二组实验,此次保持宽和高的比为1∶1,变化长度进行优化选择。实验安排如表2。
同样在不同尺寸下提取差分信号峰值进行分析,其结果如图6所示。由于长、宽因素在线圈中无特定量,即长、宽为等价的,通过对比长、宽时的曲线数据可知,当长、宽比例为2∶1时为最优比值。
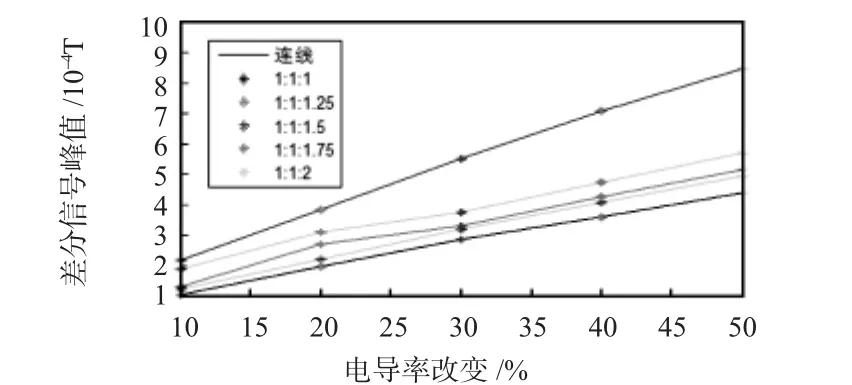
图5 不同高度下的差分信号峰值随电导率的变化Fig 5 Peak value of differential signal with height changes and conductivity changes

表2 长度变化激励线圈尺寸参数表Tab 2 Excitation coil size parameters of height change
因此,当长、宽、高综合考虑时,由于高是相对于长、宽的1.5 倍,而长、宽优化比为 2∶1,因此,对比长、宽、高比值为 2∶1∶1.5,2∶1∶3,2∶1∶2.25 时的数据,即长、宽、高尺寸分别为(40,20,30 mm),(40,20,60 mm),(40,20,45 mm),其结果如图7所示。从图7可知,当长、宽、高比值为2∶1∶1.5时,脉冲涡流矩形传感器的灵敏度、线性度最好。
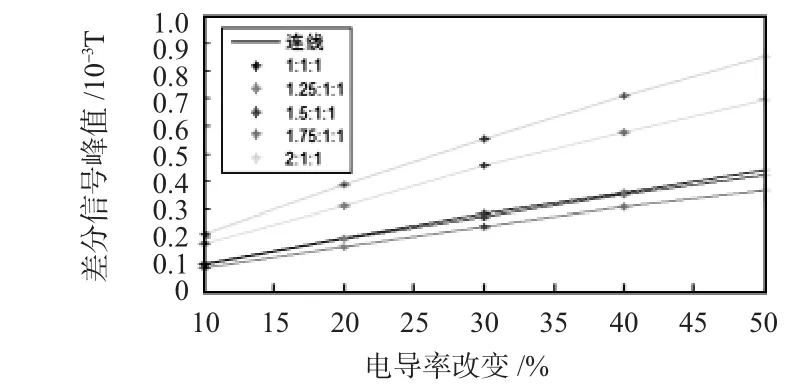
图6 长宽比值变化时差分信号峰值图Fig 6 Differential signal peak value diagram of length and width ratio change
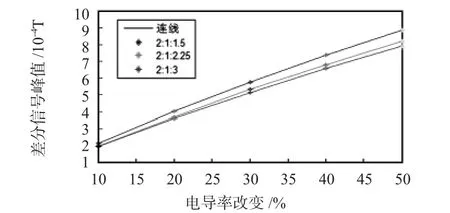
图7 三组比值的差分信号峰值图Fig 7 Differential signal peak value diagram of three groups of ratio
3 实验验证与结果分析
3.1 实验验证系统设计
根据仿真结果,实验制作了3个不同尺寸的矩形线圈骨架。按照仿真的最佳三组比例,以20 mm为基值,3个线圈骨架的尺寸分别为40 mm×20 mm×30 mm,40 mm×20 mm×45mm,40mm×20mm×60mm。使用直径为0.36mm的漆包线绕制的线圈厚度与仿真使用的厚度相同,为3 mm。验证实验采用试样的缺陷深度变化来代替电导率的变化。被测试样为铝板,尺寸(长×宽×厚)为150 mm×50 mm×10 mm。缺陷宽度为 2 mm,深度依次为 2,4,6,8 mm,实验试块如图8所示。板材厚度为10 mm,缺陷可认为电导率为0,缺陷检测实验近似模拟被测试件电导率的变化。因此,可以通过此方法来验证仿真结果。实验使用3个探头分别在没有缺陷和不同深度的缺陷处进行测量和数据采集。
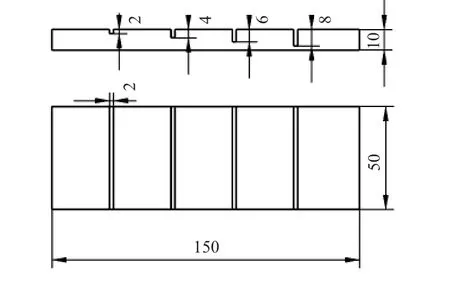
图8 试样缺陷示意图Fig 8 Schematic diagram of specimen defects
3.2 实验结果分析
本实验使用DAQ2010数据采集卡进行数据采集。采样频率为10 kHz,脉冲波的上升沿触发,采样点数为1 000点,共采集10个周期的数据。对信号进行平均处理,避免单个周期的偶然性,提高实验的精确度。采集信号后的处理步骤如图9。

图9 数据处理流程图Fig 9 Flow chart of data processing
如图10所示,原始信号中由于直流分量的存在,导致信号电压整体均在零以上。
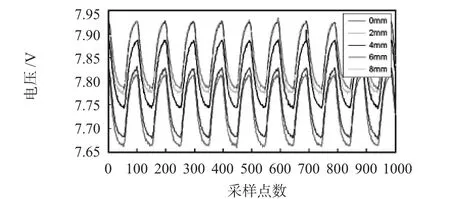
图10 采集到的原始信号Fig 10 Collected original signal
图11为原始信号减去各自的均值的结果,可以看出:对电路信号中的直流分量进行了去除。由于信号中存在一定的噪声,所以,必须经过滤波处理。经过软件滤波然后获取差分信号如图12所示,信号的噪声明显减小。将图12的10个周期的信号平均到一个周期,这样可以进一步消除噪声。其周期平均滤波结果如图13所示。
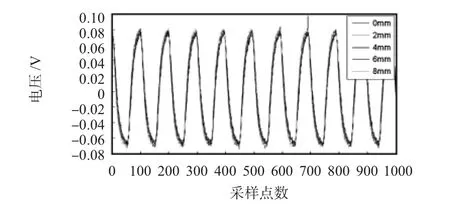
图11 原始信号减去均值得到的信号Fig 11 Signal obtained from original signal subtracted by the mean value
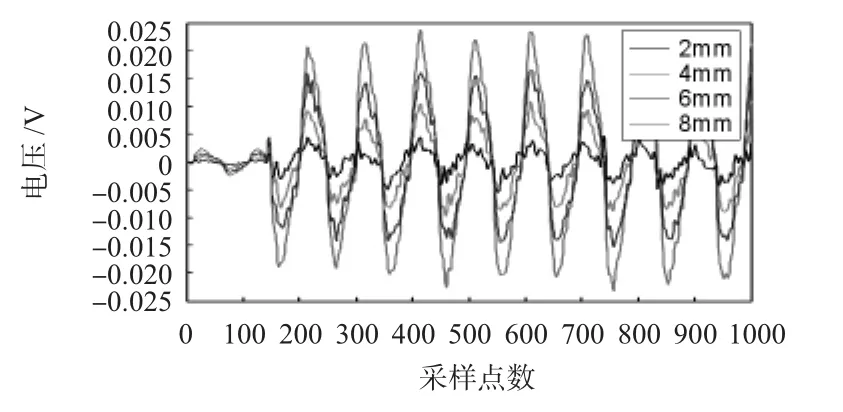
图12 差分信号Fig 12 Differential signal
从图13可以看出:随着缺陷深度的增加,差分信号峰值增大。为此,本文提取差分信号峰值进行灵敏度与线性度分析。其3个矩形脉冲涡流探头的实验结果如图14所示。从图14中可以看出:尺寸为40 mm×20 mm×30 mm的传感器线性度和灵敏度最好。实验结果验证了仿真结果的有效性,证实当长、宽、高比值为2∶1∶1.5时,脉冲涡流矩形传感器的灵敏度、线性度最好。
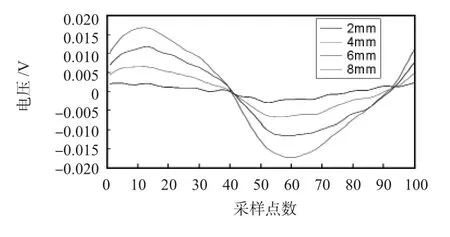
图13 平均到一个周期的信号Fig 13 Signal of averaged one period
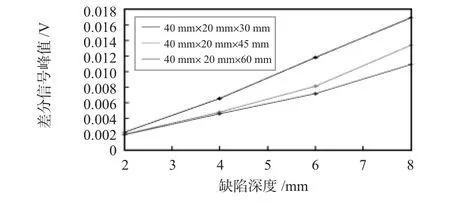
图14 不同尺寸传感器的灵敏度分析Fig 14 Sensitivity analysis of different size sensors
4 结论
本文通过仿真和实验探究了脉冲涡流矩形传感器尺寸参数对对铝板检测的灵敏度影响规律。研究发现:脉冲涡流矩形传感器灵敏度、线性度与传感器长宽、高度有关。在长宽不变的情况下,当长、宽、高比为1∶1∶1.5时,传感器的线性度和灵敏度最高;在高不变时,长、宽比为2∶1时传感器最优。通过对比 2∶1∶1.5,2∶1∶3,2∶1∶2.25 得到长、宽、高最佳比为2∶1∶1.5。本文通过对矩形传感器尺寸的仿真和实验,找出了最优化比值,有利于进一步提高脉冲涡流矩形传感器的检测性能。
[1] 杨宾峰,张 辉,赵玉丰,等.基于新型脉冲涡流传感器的裂纹缺陷定量检测技术[J].空军工程大学学报:自然科学版,2011,12(1):73 -77.
[2] 徐志远,武新军,黄 琛,等.激励参数和试样电磁参数对脉冲涡流检测的影响的仿真分析[J].无损检测,2011,30(6):1-4.
[3] Hoshikawa H,Koyama K.Eddy current distribution using parameters normalized by standard penetration depth[J].Materials Evaluation,1999,9:587 -593.
[4] Morozov M,Tian Guiyun,Withers P J.The pulsed eddy current response to applied loading of various aluminium alloys[J].NDT&E International,2010,43:493 -500.
[5] Fava J,Ruch M.Design,construction and characterization of ECT sensors with tectangular planar coils[J].Insight,2004,46(5):268-274.
[6] Greenhouse H M.Design of planar rectangular microelectronic inductors[J].IEEE T Parts Hyb Pac(PHP),1974,10(2):101 -109.
[7] Theodoulids T P,Kriezis E E.Impedance evaluation of rectangular coils for eddy current testing of planar media[J].NDT&E International,2002,35:407 - 414.
[8] He Yunze,Luo Feilu,Pan Mengchun.Defect edge identification with rectangular pulsed eddy current sensor based on transient response signals[J].NDT&E International,2010,43:409 -415.
[9] He Yunze,Luo Feilu,Pan Mengchun.Defect classification based on rectangular pulsed eddy current sensor in different directions[J].Sensors and Actuators A:Physical,2010,157:26 - 31.
[10] He Yunze,Luo Feilu,Pan Mengchun.Defect characterization based on pulsed eddy current imaging technique[J].Sensors and Actuators A:Physical,2010,164:1 - 7.
