基于图像处理的版图优化方法

宁 盼，王俊平，张广燕，曹洪花，李 锦，李长江，李 博

(西安电子科技大学通信工程学院，陕西西安 710071)

随着半导体产业和集成电路的快速发展，可制造性问题和成品率等问题随之变得日益重要。然而在光刻工艺中出现的冗余物缺陷、氧化物针孔缺陷或PN结泄露缺陷等随机缺陷经常会导致集成电路成品率的下降［1-5］。考虑随机缺陷的成品率设计的重要途径是在设计阶段，尤其是版图设计阶段，因此依赖设计减小成品率损失具有重要的意义［6-9］。

已有的实验表明，制造工艺中出现的真实缺陷不但轮廓是非规则形状［10-12］，而且还具有一定的空间分布。为便于研究成品率损失的问题，研究者提出了关键面积的概念［13-15］。通过研究短路关键面积的缩小可以实现对版图的优化，进而改善成品率。目前文献［16-18］研究了关键面积的模型与提取算法，甚至是优化线网的具体位置信息［19-20］，但并未具体实现优化线网的自动变化。文献［21］提出一种基于线性规划降低关键面积的方法。这种方法只能处理布线规则的版图，不能处理任意形状布线的版图，故本文提出了一种基于图像处理的优化版图方法。

本文通过把版图转化为图像，从图像的角度出发，结合数学形态学膨胀算法原理，通过减小短路关键面积来实现版图优化。该优化方法以待移动线网在其可移动空间中与其可视线网间的短路关键面积之和最小，作为待移动线网移动的依据来移动线网，实现短路关键面积的缩小。

1 基于图像处理版图优化算法介绍

先介绍基于图像处理实现版图优化的理论依据，再介绍实现版图优化算法和其中的核心算法—可移动空间算法。

1.1 版图优化理论依据

基于图像处理实现版图优化的思想来源于文献［20］中关键面积提取模型。在该模型中，版图用两维版图矩阵表示，利用数学形态学中膨胀算法来提取关键面积。故本文的优化算法就是以图像相关理论和膨胀算法作为理论依据。从图像角度来研究线网间短路关键面积的缩小，相当于把版图上的线网看作图像上的前景信息，短路关键面积看作是这些前景信息间的某种关系，短路关键面积的缩小就是通过对图像上的前景信息做相应的处理来实现。

1.2 版图优化算法介绍

从图像的基本组成和膨胀算法基本原理出发，实现版图优化的算法，其关键步骤是确定待移动线网及其可移动空间，并找到待移动线网的最佳移动位置。基于图像处理实现版图优化的流程如图1所示。

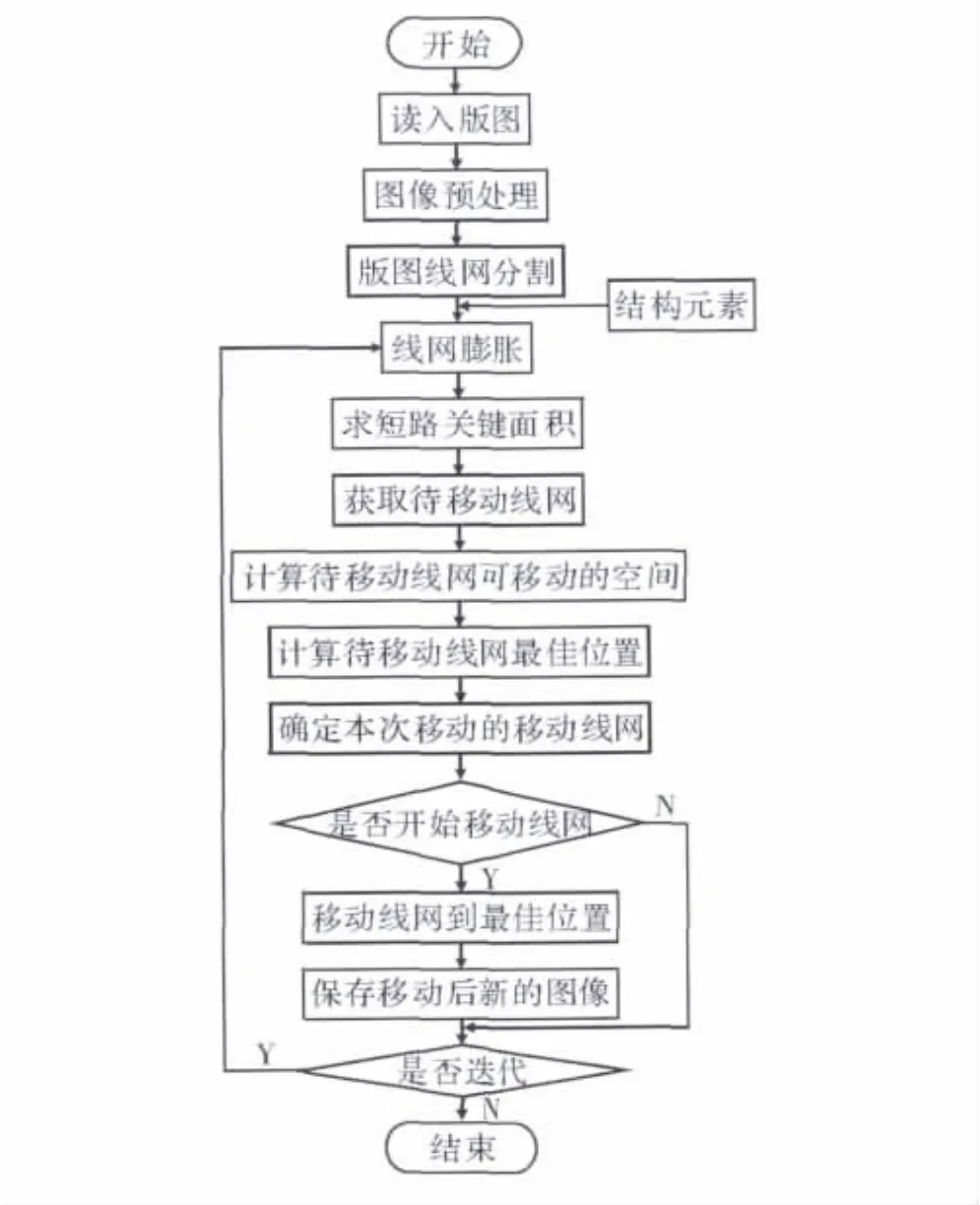
图1 版图优化算法流程图

在此算法中，先读入版图信息，获得版图矩阵，利用文献［20］中的模型提取短路关键面积。在所有短路关键面积中，找出线网间短路关键面积最大的两个线网，作为待移动线网。再计算待移动线网与周围线网上下左右可移动的距离，即确定了可移动空间。在可移动空间中，逐一在每个位置移动待移动线网，确定短路关键面积减小最大的位置，作为待移动线网的最佳移动位置。然后比较两个待移动线网移动到最佳移动位置时减小的关键面积，把关键面积减小最大的待移动线网作为本次移动的线网。获得具体的移动线网和最佳移动位置后，就可以移动线网实现版图优化。循环该算法，直到达到要求为止。

1.3 可移动空间算法介绍

可移动空间是线网的移动范围，该范围保证了在可移动空间中移动线网不会与可视线网相重叠。线网可移动空间算法是实现优化算法中的一部分。在介绍这段算法前，假设已经做好前序处理。待移动线网的可移动空间算法如下:输入，短路关键面积CA(N)和待移动线网NetNum;N为线网个数。输出，待移动线网 NetNumde 可移动空间［UpDis，DownDis，LeftDis，RightDis］。

(1)输入待移动线网NetNum。

(2)确定待移动线网NetNum的可视线网RoundNet。

当线网号i＜NetNum，if(CA(i).ca(j)≠0)，则RoundNet=［RoundNeti］，i=1，…，NetNum-1，CA(i).net(j)=NetNum，j为与线网i存在短路关键面积的线网个数;

当线网号i＞NetNum，则 RoundNet=［RoundNeti］，i=CA(NetNum).net(j)，j为与线网 NetNum 存在短路关键面积的线网个数。

(3)提取待移动线网NetNum轮廓的坐标boundary(x，y)和所有可视线网 RoundNet［i］的轮廓坐标b［k］(x，y);k为可视线网的个数。

(4)求待移动线网NetNum轮廓boundary(x，y)中x和y的最小值 min(x，y)和最大值 max(x，y)，min(x，y)=findmin(boundary(x，y))，max(x，y)=findmax(boundary(x，y))。

(5)计算待移动线网NetNum的水平可视线网HorNet［］和竖直可视线网 VerNet［］。

当 min(x)或 max(x)b［i］(x，:)中，则线网i为竖直可视线网;当 min(y)或者 max(y)b［i］(:，y)中，则线网i为水平可视线网。

(6)获取待移动线网NetNum的上下左右可视线网 UpNet，DownNet，LeftNet，RightNet。

若y∈boundary(x，y)，boundary(x，:)＜b［i］(x，:)，则线网i为待移动线网NetNum的左可视线网LeftNet=［LeftNeti］;

若y∈boundary(x，y)，boundary(x，:)＞b［i］(x，:)，则线网i为待移动线网NetNum的右可视线网RightNet=［RightNeti］;

若x∈boundary(x，y)，boundary(:，y)＜b［i］(:，y)，则线网i为待移动线网NetNum的上可视线网Up-Net=［UpNeti］;

若x∈boundary(x，y)，boundary(:，y)＞b［i］(:，y)，则线网i为待移动线网NetNum的下可视线网DownNet=［DownNeti］。

(7)计算待移动线网NetNum的上下左右可移动距离 UpDis，DownDis，LeftDis，RightDis。

LeftDis=findmin(max(b［j］(x，:))，min(NetNum［x］))，jLeftNet［］;RightDis=findmin(min(b［j］(x，:))，max(NetNum［x］))，jRightNet［］;UpDis=findmin(max(b［j］(:，y))，min(NetNum［y］))，jUpNet［］;DownDis=findmin(min(b［j］(:，y))，max(NetNum［y］))，jDownNet［］。

(8)输出待移动线网 NetNum的可移动空间［UpDis，DownDis，LeftDis，RightDis］，上下左右可移动距离 UpDis，DownDis，LeftDis，RightDis 分别减去线网间最小间距即为可移动空间。

输入需确定可移动空间的线网，判断是否存在可视线网。线网可视线网的判断依据，就是是否与该线网存在短路关键面积，若存在，则为可视线网;否则，不是可视线网。根据线网与其可视线网在图像中所处的像素位置，来判断可视线网中哪些线网为线网的上可视线网、下可视线网、左可视线网和右可视线网。具体实现方法就是通过先对线网的每一列进行遍历，如果某个可视线网存在线网中任意一个列坐标的像素，则为水平可视线网;同样对线网的每一行进行遍历，如果某个可视线网存在线网中任意一个行坐标的像素，就为竖直可视线网。再进一步判断，如果线网中该列坐标对应的行坐标大于水平可视线网中该列坐标所对应的行坐标，则为左可视线网;若小于，则为右可视线网;如果线网中该行坐标对应的列坐标大于竖直可视线网中该行坐标所对应的列坐标，则为上可视线网;若小于，则为下可视线网。

判断出上下左右4个方向的可视线网，就可以计算待确定线网的可移动空间。在所有的左可视线网中，计算与需确定可移动空间线网的最短距离，再减去线网间的间宽，即为左边可移动距离;同理，右可移动距离，上可移动距离和下可移动距离为右、上和下可视线网中与需确定可移动空间线网的最短距离减去线网间的间宽。这4个距离以线网为中心，就构成了线网的可移动空间。图2所示是一个待确定可移动空间线网的可移动空间，其中灰色区域就是需判断待确定可移动空间线网的可移动空间。

图2 线网的可移动空间图例

得到可移动空间后，接下来需要在可移动空间中找到一个最佳位置，也就是具体实现短路关键面积缩小算法。

2 基于图像处理版图优化算法实现

结合具体版图介绍线网移动的最佳位置。线网移动的最佳位置可以通过计算线网的最佳移动距离来表示。找出最佳移动位置最直接的方法就是对可移动空间中的每一个位置进行试探，计算出线网处在可移动空间的每个位置与可视线网形成的短路关键面积，并与移动前与可视线网形成的短路关键面积之和求其差值，找出所有差值中的最大值，则其对应的位置就是最佳移动位置，这种方法称之为可移动空间试探法。在可移动空间试探法中，由于线网的移动，可能会与其他原本没有短路关键面积的线网产生短路关键面积，把这些线网称之为新可视线网。然后在移动的过程中判断与所有可视线网的短路关键面积减少的最大值，那么这个最大值所处的位置就是最佳移动位置。

假定缺陷为D(d1，d2)，移动线网为i，线网i上下左右可移动的距离分别表示为:UpDis(i)、DownDis(i)、LeftDis(i)、RightDis(i)。对于所有线网i的可视线网的线网j:如果线网i的最大行与线网j的最小行之差或者线网j的最大行与线网i的最小行之差大于d1加上UpDis(i)与DownDis(i)的最大值，或线网i的最大列与线网j的最小列之差或者线网j的最大列与线网i的最小列之差＞d2加上LeftDis(i)与RightDis(i)的最大值，则线网j是线网i移动后可视线网。

对图3(a)所示的版图进行优化，结果见表1和图3，图中的红色线网表示本次优化过程中移动的线网。假定线间最小距离为10u(u为线网间的距离单位)。

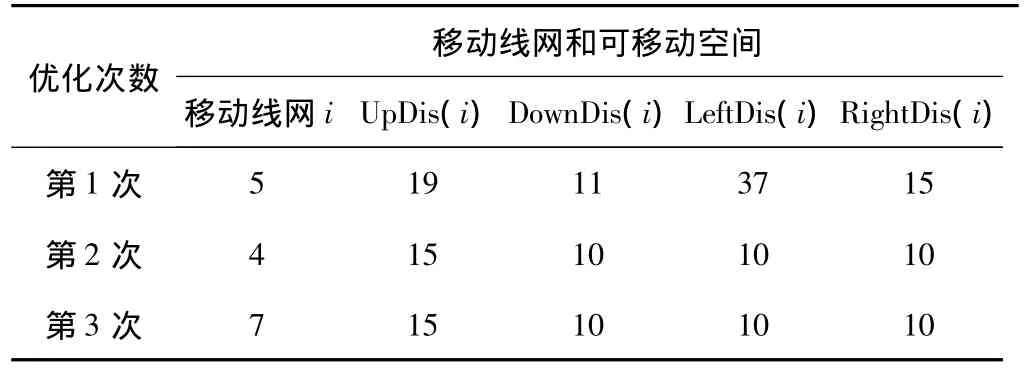
表1 优化次数和移动线网及其可移动空间

两次优化后的总短路关键面积如表2所示，其中SNetCA表示总短路关键面积，FSNetCA表示优化前总短路关键面积，HNetCA表示优化后总短路关键面积，u2为短路关键面积的度量单位。

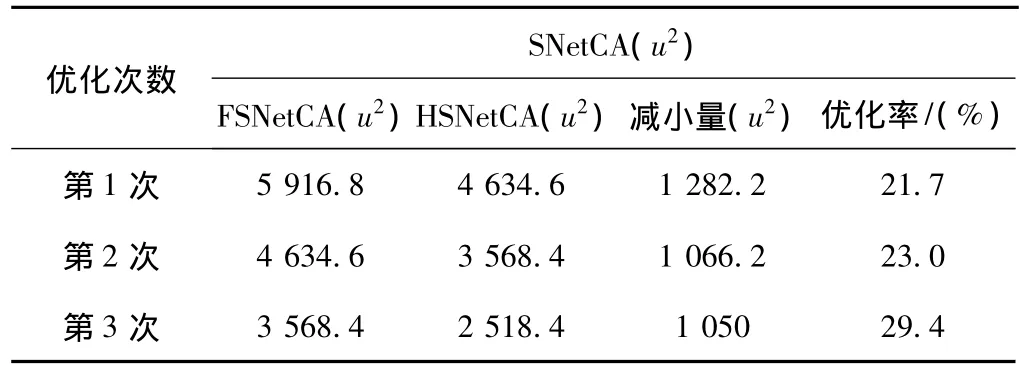
表2 可移动空间试探法三次优化后的总短路关键面积

图3 三次优化的结果

从以上数据可以看出通过可移动空间试探法实现短路关键面积的缩小，达到了优化版图的目的。这种方法操作比较简单，优化版图的效果比较明显。

3 结束语

依据图像处理和数学形态学中的膨胀算法原理，提出了一种基于图像处理的版图优化方法。该方法通过确定待移动线网及其可移动空间，并在可移动空间中找到最佳移动位置来移动线网以减小短路关键面积，实现了版图优化。这种算法不但考虑了缺陷的真实轮廓特征，况且不受线网形状的制约，具有广泛的适用性。另外，该算法实现自动优化线网的变化，更有利于版图的优化。

［1］LUECK M R，REED J D，GREGORY C W，et al.High-density large-area-array interconnects formed by low-temperature cu/sn-cu bonding for three-dimensional integrated circuits ［J］.IEEE Transactions on Electron Devices，2012，59(7):1941-1947.

［2］ABBAS Z，YAKUPOV M，OLIVIERI N，et al.Yield optimization for low power current controlled current conveyor［C］.SBCCI 30 IEEE，2012，Aug.-2 Sep.-5.

［3］沙建超，暴洪成.浅谈集成电路国内外技术现状及发展趋势［J］.民营科技，2011(12):52.

［4］张国霞，马佩军，张旭，等.集成电路关键面积研究方法的发展与挑战［J］.微电子学，2009，39(5):704-709.

［5］王俊平，郝跃，任春丽.椭圆缺陷轮廓的关键面积计算模型［C］.郑州:2008年(第十届)中国科协年会，2008.

［6］GAO X，MACCHIARLO L.Track routing optimizing timing and yield:Design Automation Conference(ASP-DAC)［C］.2011 16th Asia and South Pacific，2011:25-28.

［7］Yu-Wei L，Yen-Hung L，Yih-Lang L.Gridless wire ordering，sizing and spacing with critical area minimization［C］.ISQED 2011，2011:14-16.

［8］MULLER D.Optimizing yield in global routing［C］.IEEE/ACM International Conference on Computer-Aided Design，Digest of Technical Papers，ICCAD，2006:480-486.

［9］MINSIK C，HUA X，PURI R，et al.TROY:track router with yield-driven wire planning:design automation conference［C］.44th ACM/IEEE，2007:4-8.

［10］张俊明.成品率估计与提升技术研究［D］.西安:西安电子科技大学，2009.

［11］FONG L C，CHIN A.Failure analysis on plasma charging induced damage due to effect of circuit layout device structure marginality ［C］.Piscataway，NJ，USA:IEEE.IPFA 2012，2012.

［12］JANSEN S，FLORENCE G，PERRY A，et al.Utilizing design layout information to improve efficiency of SEM defect review sampling［C］.Cambridge，MA，United States:ASMC Proceedings，2008.

［13］赵天绪，段旭朝，马佩军，等.基于关键面积的冗余集成电路成品率分析［J］.半导体学报，2003，24(5):544-549.

［14］马佩军.集成电路功能成品率仿真与优化技术研究［D］.西安:西安电子科技大学，2000.

［15］陆勇.集成电路功能成品率模型及参数提取方法的研究［D］.西安:西安电子科技大学，2002.

［16］王俊平.集成电路功能成品率的估计模型研究［D］.西安:西安电子科技大学，2005.

［17］王俊平，郝跃，张卓奎，等.椭圆缺陷轮廓的成品率估计［J］.西安电子科技大学学报:自然科学版，2006，33(3):433-437.

［18］MINSIK C，HUA X，PURI R，et al.Track routing and optimization for yield［J］.IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems，2008，27(5):872-882.

［19］WANG Junping，REN Guangliang，NI Hao.WCA with size and space distribution of real defects for 65-90 nm［C］.2008 2nd International Conference on Anti-Counterfeiting，Security And Processes，2008:181-184.

［20］王俊平，郝跃.65～90 nm技术节点的WCA模型和提取算法［J］.物理学报，2009(6):4267-4273.

［21］王强，王俊平，任春丽.基于线性规划的关键面积缩小算法研究［J］.电子科技，2008，21(10):1-4.