基于LabVIEW的圆度误差算法实现

2013-10-17冉子龙

电子科技 2013年7期

冉子龙

(合肥工业大学仪器科学与光电工程学院，安徽合肥 230009)

圆度仪是用于测量圆度误差，而圆度误差的评定算法有多种，每种算法又可由不同的方法实现，不同的算法和方法均有不同的精度和速度。本文采用一种迭代求优法，并由LabVIEW实现，该算法以最小二乘圆的圆心作为初始圆心，将交叉弦法和中心最佳移动法相融合，通过计算得到最小移动步长和最佳移动方向，不断移动圆心以达到更精确、快速地逼近理想圆心的目的。

1 最小区域圆法圆度误差判断准则

根据国家标准GB1183-75，圆度误差是包容同一横截面轮廓并且半径之差为最小的两个同心圆间的距离［1］。最小区域圆法定义:得出两个同心圆，要完全包容工件轮廓，并且这两个同心圆具有最小的半径差。交叉弦法原理:以被测轮廓上两交叉弦的各自垂直平分线的交点为圆心，并通过各自弦的端点做两个同心圆，然后用轮廓上的另一条弦替换二弦之一，使同心圆圆心随之变动，直至同心圆包容整个轮廓。

根据圆度误差和最小区域圆法的定义以及交叉弦法原理可得最小区域圆法判断准则:两个同心的最大、最小包容圆与显示轮廓相接处至少有相间4点。并且最大包容圆上两接触点的连线与最小包容圆上两接触点的连线相交叉，又称交叉准则。而圆度误差为这两同心圆半径之差［2］。

2 最小区域圆法算法

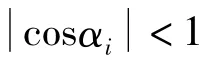
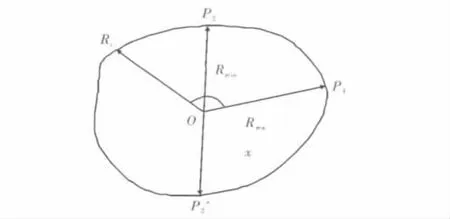
图1 实际轮廓

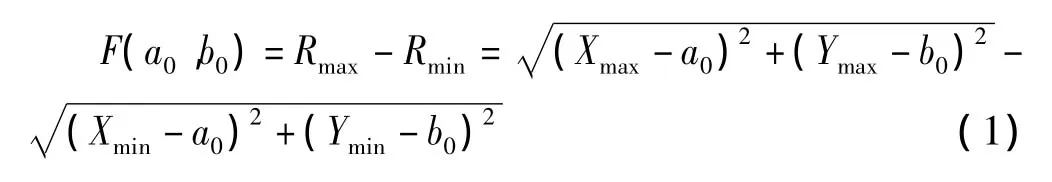
其中，O0(a0，b0)为移动后的圆心;圆度误差=F(a0，b0)min=F(a'，b')，因此，确定理想圆心O'(a'，b')是得到圆度误差的关键。

2.1 计算最小二乘圆的圆心

通过最小二乘圆法计算得出最小二乘圆的圆心作为本算法的初始圆心。用最小二乘圆的圆心作为初始圆心，是因为它比测量圆心更接近理想圆心［3］。

2.2 圆心移动方向的确定

由于最小区域圆法要求Rmax值尽可能小，Rmin尽可能大，很显然，使圆心O向最大距离点矢量方向即OP1方向移动可以减小Rmax值，而向最小距离点矢量方向即OP2反方向移动可以增大Rmin值。所以圆心最佳移动方向为OP1和OP'2，这里设定先OP1，后OP'2［4-5］。

2.3 移动步长的确定

步骤1 让圆心先向OP1方向移动ΔRmax，设移动了，各点到新圆心的距离变化了

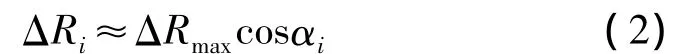
式中，cosαi为圆心到各点的矢量与OP1的夹角余弦值，其值可由式(3)计算

要让移动后的Ri值等于Rmax值，需要移动值，此值可由式(4)计算

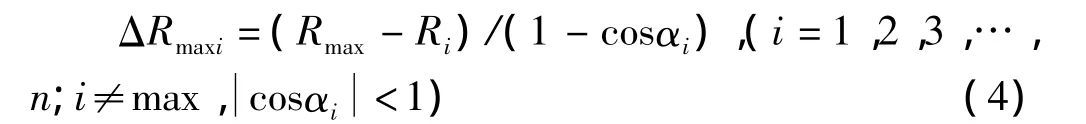
在计算出的值中选出最小值作为最佳移动步长ΔM，并得出新的圆心

式中，αmax为OP1与X轴的夹角;a、b为初始圆心的横坐标与纵坐标;a0、b0为新圆心的横坐标与纵坐标。

步骤2 再让圆心往OP2反方向移动。注意此时的OP2为移动圆心后重新计算出来的Rmin的矢量方向。相似的，移动量可以写成

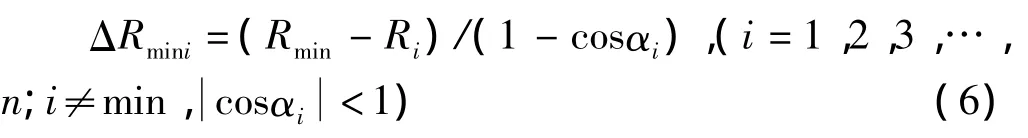
式中，cosαi为Ri与OP2的夹角余弦值，其值由式(7)得到

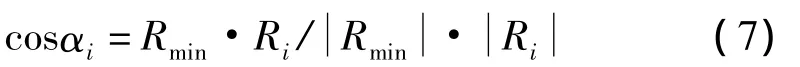
由于Rmin-Ri＜0，所以 ΔRmini＜0，用其中的最大值(即绝对值最小)作为最佳移动步长ΔM，并用式(4)得出新的圆心坐标。

2.4 判断并算出圆度误差

用最后的圆心算出两最大值与最小值，并判断两最大值的连线和两最小值的连线是否相交于线段内。若不在，则重复2.3节中的步骤。若在，则计算出两线段的垂直平分线的交点是否为理想圆心，是的话得出圆度误差，F=Rmax-Rmin;若不是，用所得的交点作为圆心重复2.3节中的步骤并进入2.4中判断。

最小区域圆法程序流程如图2所示，最小区域圆法的程序流程比较复杂，不仅要求4个点，且还有两个判断、两个循环。相比最小区域圆法，最大内切圆法程序流程，则较为简单，只需求3个最小值点，且只有一个循环，如图3 所示［6］。

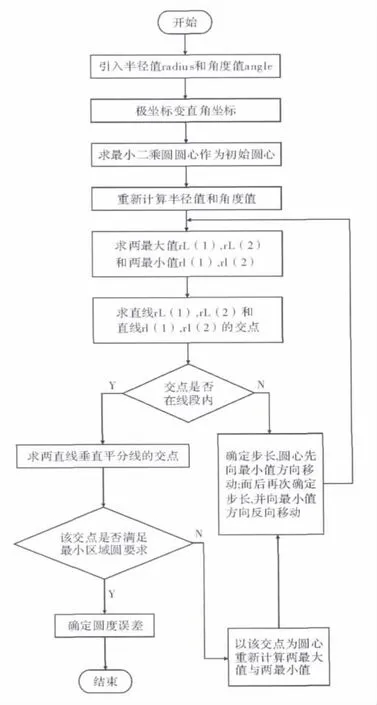
图2 最小区域圆法

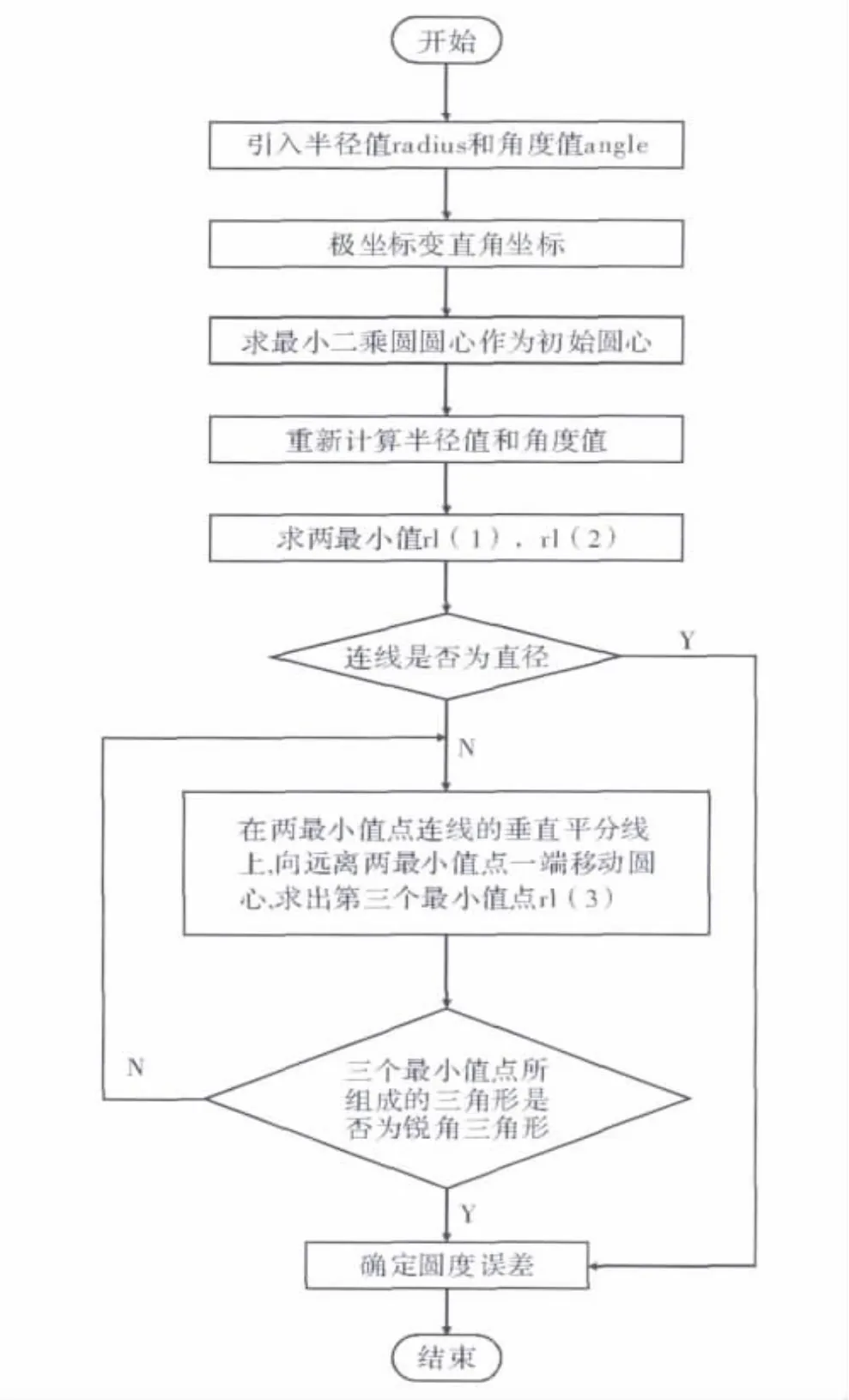
图3 最大内切圆法

3 最小区域圆法LabVIEW实现

用LabVIEW实现上述流程的优点有:LabVIEW前面板的虚拟仪器控件直观、易操作，可以方便地控制数据采集及圆度误差评定等过程。图4为用LabVIEW主程序进行测试时的LabVIEW前面板，为使实际轮廓清晰，降低了采样点数，图中曲线3为工件的实际轮廓，曲线1为最大包容圆，曲线2为最小包容圆［7-8］。

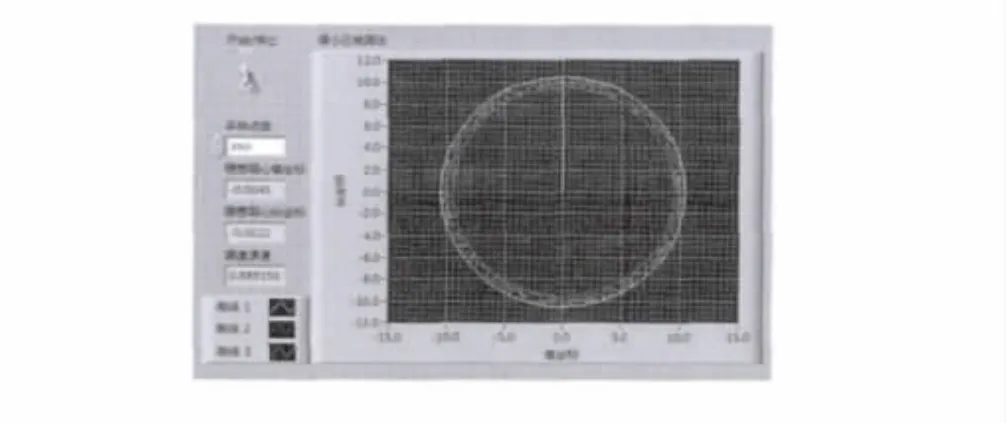
图4 最小区域圆法运行结果

4 最大内切圆法圆度误差判断准则

最大内切圆法判别准则有两个:其一为3点法，即内切圆至少与被测圆有3点接触，且这3点构成锐角或直角三角形;其二为两点法，即内切圆与被测圆仅有二点接触，且圆心在这两点形成的直线上，然后找出此内切圆外部的另一同心圆，使得两同心圆恰好能够包容轮廓，此时两同心圆半径差即为圆度误差［2］。此准则来源于圆度的定义、最大内切圆法定义以及锐(直)角三角形准则。

5 最大内切圆法算法

最大内切圆法与最小区域圆法基本一致，不同的是最大内切圆法只需要求3个最小值即可。

经步骤2.1后进入步骤2.3中第二步，得出两最小值。判断两最小值的连线是否为理想圆的直径，如果是，则评定圆度误差。若不是，则寻找第3个最小值点，此时可以肯定圆心在这两个最小值点连线的垂直平分线上。因此，圆心沿这条垂直平分线、远离两极值点的方向移动，经验证，初始步长设定为step=(Rm-∑Ri/n)×0.618，以后为step0=step×0.6182。每移动一次，算出极小值点，判断此点和已得到的两个最小值点所组成的三角形是否为锐角三角形，若不是，则继续移动;若是，则此点为第3个最小值点，即对圆度误差进行评定。