一种基于误差相关函数的改进变步长LMS算法

王崇辉，邹 鲲

(1.陕西广播电视台发射部，陕西西安 710061;2.空军工程大学信息与导航学院，陕西西安 710077)

最小均方(Least Mean Square，LMS)算法是由Widrow和Hoff于1960年提出的［1］，该算法是基于最小均方误差准则的维纳滤波器和最陡下降法。LMS算法特点是计算量小、易于实现，因此获得广泛应用。LMS算法中，要提高收敛速度，步长应该尽量选择较大值，而为降低稳态方差，步长应该选择较小值。因此在LMS算法应用中，只能折衷设定步长大小，不能同时满足快的收敛速度和小的稳态方差的要求［2］。

针对LMS算法的不足，人们提出了各种的变步长(Variable Step Size，VSS)LMS 算法［3-4］。所谓VSSLMS算法，就是在算法的迭代过程中，根据当前系统的状态信息，动态改变步长的大小，从而提高收敛速度的同时还可以降低稳态方差。一般在收敛开始阶段，要求步长较大，从而提高过渡到稳态的收敛速度。在收敛结束后，需要小的步长，这样可以减小由于步长较大而引入的失调，即稳态方差。

在这些VSSLMS算法中，有一类是将步长与瞬时误差平方相关联［5］，因为瞬时误差平方在收敛开始时较大，而在收敛结束后较小，称为E-LMS算法。另一类算法则是将步长与误差的相关函数相关联［6］，因为在收敛开始时，误差中间的相关分量较大，而处于稳态时，可以假定误差分量不相关，称为R-LMS算法。由于系统不可避免的引入其他噪声分量，而E-LMS算法中由于瞬时误差平方中包含噪声分量，导致该方法的抗噪性能较差，而R-LMS算法则是由于相关函数具有“记忆”效应，导致当系统性能突变时，跟踪能力较差。为此文中结合E-LMS算法中的变步长策略，对R-LMS算法进行了改进，改进后的算法在抗噪性能和跟踪性能都得到了较大的提高。

1 VSSLMS的基本原理

以系统辨识［7］为例来讨论VSSLMS算法。自适应滤波器配置方式如图1所示。输入信号为x(n)，参考信号d(n)是未知系统的输出y(n)和加性噪声分量v(n)的叠加。而由参考信号与自适应滤波器输出信号之差构成误差信号e(n)来控制自适应滤波器中的系数，对于LMS算法，就是通过调节滤波器系数，使得均方误差最小。

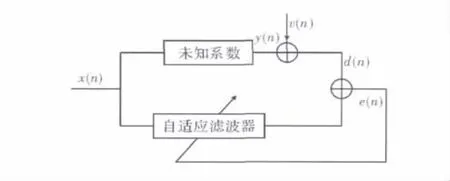
图1 自适应滤波原理图

LMS算法中的自适应滤波器系数迭代关系为

为此提出了多种VSSLMS算法，其基本思路就是将步长大小与迭代过程中的某种状态变量关联，利用状态变量的变化来动态控制步长的变化。这些状态变量可以是瞬时误差，瞬时误差的平方，相邻两次迭代的瞬时误差的相关函数，误差与输入矢量的相关性等［8］，这些状态变量在收敛开始时可能较大，而在收敛后可能较小，因此满足动态控制步长的要求。其次关联的方法也多种多样，可以是线性或者非线性的，也可以是递归或非递归的。其中非线性关联方式计算量比线性关联要大，递归关联相对于非递归关联，需要更多的存储空间。

这些VSSLMS算法当中，有一类是将步长与瞬时误差平方相关联，称之为E-LMS算法。关联的方式通常是非线性非递归形式，其算法为

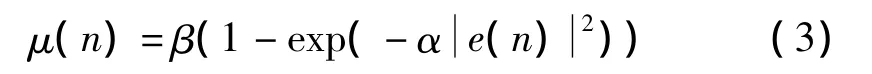
图2为该方法的学习曲线和常规的LMS算法的比较，可以看出，稳态方差比LMS算法要高，尤其是当SNR较低时，稳态方差更大，因此该方法的抗噪性能较差。

图2 不同SNR下，E-LMS算法与LMS算法的学习曲线

另一类算法是将步长与相邻两次迭代的瞬时误差的相关函数相关联，称之为R-LMS算法，采用的是线性递归形式，其算法为

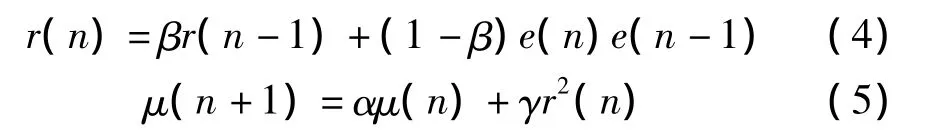
其中，0＜β，α ＜1，λ≪1，通过选择合适的参数，也可以得到较为理想的性能。式(4)是一个计算相关函数的公式，其中参数β通常称为遗忘因子，如果参数β较大，则说明该算法具有一定的“记忆”能力，也就是对当前的输入不敏感。为获得较为精确的相关函数，β通常尽可能地接近1。但当算法处于稳态时，系统内部发生突变，则这时的e(n)e(n-1)可能很大，此时应具有较大的步长，尽快过渡到收敛状态。但由于式(4)具有一定的记忆能力，因此对相关函数计算值的影响不大，因此利用式(5)计算出的步长还是维持在很小的值附近。这就说明该算法对于突变系统的跟踪能力较弱。

图3表示SNR=20 dB条件下，R-LMS算法的跟踪能力，假定在迭代次数达到750点处，未知系统的参数发生改变。如图3所示，虽然开始时，R-LMS比LMS算法有更快的收敛速度，但是一旦系统发生突变，R-LMS算法的收敛速度将缓慢。

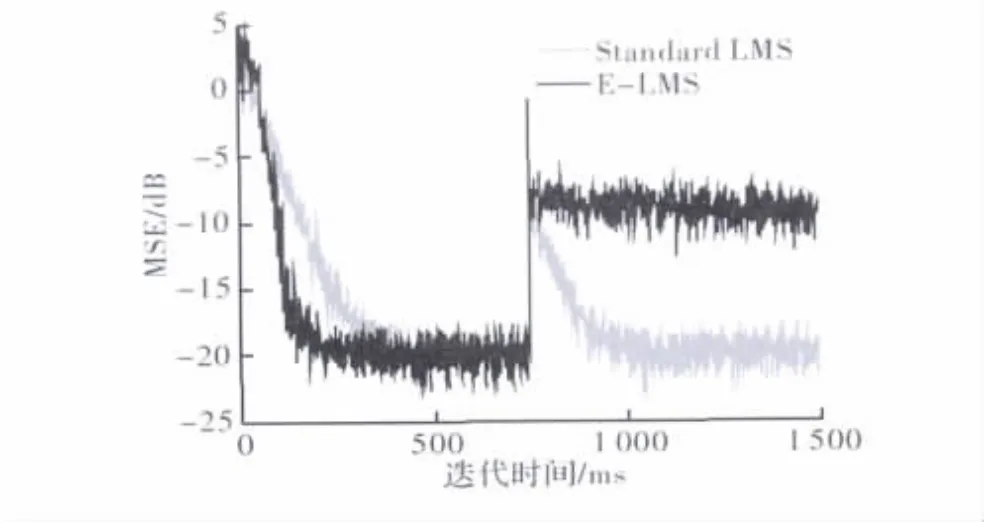
图3 R-LMS算法的跟踪能力与LMS算法对比

2 改进的VSSLMS算法

可以看出，影响R-LMS算法的主要因素来自与式(4)中的遗忘因子β，正是由于其接近1，使得相关函数的计算具有较强的记忆能力，从而对系统参数突变引入的较大误差分量不敏感。参考E-LMS算法，如果参数β能够误差平方满足一定的关联方式，就可以使得当系统突变时，适当减小β值，使相关函数的计算遗忘能力增强。本文给出的算法为

式(6)～式(7)实际是综合了E-LMS算法和RLMS算法两种控制步长的策略。其中式(7)，式(8)与R-LMS算法的步长设置完全一致，唯一不同的是因子β不是常量，因子β的控制也是通过迭代过程实现的，其控制方式与E-LMS算法中的式(3)类似，与瞬时误差功率有关。这样，本文所给出的算法中，参数β不再保持常数，而是受误差平方的控制，从而使得误差相关函数计算的记忆能力能够调整，相对于R-LMS算法，可以改善算法针对突变系统的跟踪能力，同时步长与误差相关函数关联，而不与误差平方相关联，相对于E-LMS算法有更好的抗噪声能力。

图4是本文算法的抗噪性能分析，和图2给定的条件一样，与常规LMS算法进行对比，可以看出该算法的稳态方差与LMS算法基本相等，而与图2对比可以看出，E-LMS算法随着SNR降低，稳态方差显著增大。因此可以确定该算法的抗噪性能优于E-LMS算法。

图5是本文算法的跟踪突变系统的能力分析，和图3给定的条件一样，但是当系统发生突变时，本算法能够及时跟踪，并快速进入到稳态条件，说明本算法的跟踪能力优于R-LMS算法。

图4 改进的VSSLMS算法的抗噪能力分析

图5 改进的VSSLMS算法的跟踪能力分析

3 结束语

常规LMS算法的固有矛盾是收敛速度和稳态方差无法同时满足，为此人们研究了各种VSSLMS算法，其中E-LMS算法是将步长与输出误差平方相关联，该方法抗噪能力有限，R-LMS算法则是将步长与输出误差的相关函数相关联，该方法的跟踪突变系统能力有限。本文给出了改进的VSSLMS算法，能够克服E-LMS算法和R-LMS算法的缺点，从仿真结果来看，抗噪能力优于 E-LMS算法，跟踪能力优于R-LMS算法。

［1］WIDROW B，STEARNS S D.Adaptive signal processing［M］.Prentice Hall，NJ:Englewood Cliffs，1985.

［2］HAYKIN S.Adaptive filter theory［M］.3rdEdition.New York:Prencice-Hall，1996.

［3］HARRIS R W，CHABRIES D M，BISHOP F A.A variable step adaptive filter algorithm［J］.IEEE Transaction on A-coustics Speech and Signal Proc，1986，34(4):309-3l6.

［4］KWONG R H，JOHNSTON E W.A variable step size LMS algorithm ［J］.IEEE Transaction on Signal Processing，1992，40(7):1633-l642.

［5］SHAN T J，KALLAITH T.Adaptive algorithm:an automatic gain control feature［J］.IEEE Transaction on Acoustic，Signal Processing，1991，35(1):122-127.

［6］蒋明峰，郑小林，彭承琳.一种新的变步长LMS自适应算法及其在自适应噪声对消中的应用［J］.信号处理，2001(3):282-286.

［7］罗小东，贾振红，王强.一种新的变步长LMS自适应滤波算法［J］.电子学报，2006，34(6):1123-1126.

［8］高鹰，谢胜利.一种变步长LMS自适应滤波算法及分析［J］.电子学报，2001，29(8):1094-1097.