一种基于训练序列的OFDM定时同步算法

史铭宇

(哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨 150001)

OFDM(Orthogonal Frequency Division Multiplexing)技术是将一个高速串行数据变换为多个并行低速的子载波上的低速数据，有效降低频率选择性衰落对信号的影响，OFDM将成为下一代无线通信的核心技术，但由于OFDM信号的生成原理，系统内存在多个正交的子载波，其输出为多个正交子载波信号的叠加，符号性能受到载波偏移的影响比单载波系统更加敏感，所以子载波之间的正交性是接收端能够进行OFDM正确解调的关键。因此，利用同步算法，降低符号定时和载波频率的不同步对系统性能的影响是OFDM的关键技术之一。近年来，国内外已有多人提出关于OFDM的同步算法。Van de Beek［1］提出利用循环前缀的一种最大似然算法。Schmidl和Cox提出一种利用训练序列进行同步的算法［2］，该算法的训练序列由PN序列即伪随机序列来产生，该同步算法中定时同步会出现一个峰值平台从而导致定时准确性不高。Hlaing Minn［3］提出一种新的训练序列，解决了Schmidl算法中的峰值平台问题，但定时度量曲线存在多个尖峰，从而导致定时不准确。Park基于上面的理论提出一种新的训练序列［4］，Park算法可在正确的定时位置产生一个比较尖锐的高峰，但定时度量函数曲线依然存在多个尖峰。文中提出一种新的算法，该算法使用一种新的训练序列，与以往基于训练序列的OFDM同步算法不同，该序列不使用PN序列而使用具有较好自相关性的chu序列［5-6］来产生，降低了循环前缀对定时度量函数的影响，有效解决了峰值平台及多峰值问题，定时度量曲线只产生一个单脉冲，正确指出了符号的定时位置。

1 系统模型

在OFDM系统中，发送端的基带时域传输信号可表示为

其中，n=-Ng，…，0，1，…，N-1;Xk为调制到第k个子载波上的数据;N为系统中子载波数目;Ng为循环前缀的长度。

考虑到接收信号的延迟、频率偏移和高斯噪声的影响，接收信号可表示为

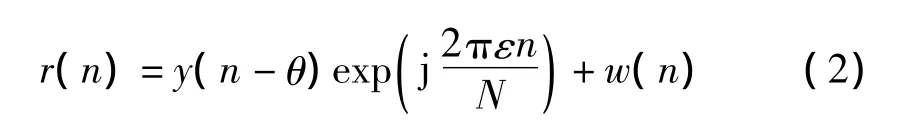
θ和ε分别表示延迟的样点数和归一化的频率偏移值;w(n)表示加性高斯白噪声，其均值和方差分别为0和 σw。

2 chu序列简介

周期为Nc的chu序列的形式如下

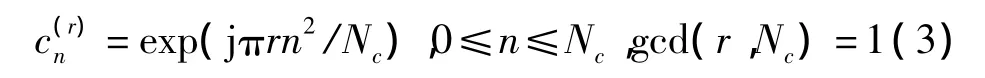
其自相关特性满足

整数频偏的估计利用训练序列的相关性，使用chu序列来实现信号的粗频率偏差估计。

假设系统存在整数频偏，设整数频偏因子为εi，此时chu序列的相关特性将改变，此时chu序列的相关特性如下

其中的

由上述内容可得，在存在大频偏的情况下，chu序列的相关值会发生移位，具体的移位大小根据系统中的整数频偏大小确定。利用该方法，便可根据具体的系统定时位置的偏移信息估计出系统存在的整数频偏大小，本算法中此种操作借助了周期为N的chu序列来帮助计算。按此操作虽增加了帧的长度，但相比起传统的估计算法，本算法无须进行FFT计算，就实现了只在时域中进行估计。运用该算法所求出的整数频偏的估计范围是受限的，具体受限范围跟所采用的chu序列相关峰值的移位大小有关。

3 Schmidl定时同步算法

目前阶段所出现的基于训练序列的定时算法中，美国斯坦福大学的Schmidl＆Cos在1997年提出基于训练序列的OFDM定时和频偏估计算法较为经典。在日后所出现的大多以训练序列辅助估计OFDM同步的算法中，其基本思想均是在SC算法上进行改进的。

该算法利用了两个码元长度的训练序列作为帧头，其中第一个序列用来做帧同步和估计小数频偏，第二个训练序列用以估计信号和整数倍频偏。文中讨论第一个训练序列。

图4 SC算法的训练列结构

训练序列1长度与OFDM符号长度相等，分为前后相同的两部分序列A和A，各占N/2的长度，训练序列由PN序列产生。在经历信道传输后，这两部分训练序列在时域中依然相同，仅存在由载波频偏引起的相位偏差。训练序列2的长度也是N。CP1、CP2由训练序列产生的循环前缀，CP是传输数据的循环前缀，长度均为L。

该算法定时估计点的确定是通过寻找定时估计函数M(d)的最大值来实现的

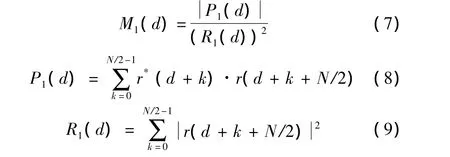
该定时算法的原理是采用延时相关算法，即找出前后两部分的最大相关点，并将其作为OFDM符号的起始点。

4 新算法

算法采用chu序列生成训练信号，训练序号分为两部分，第一部分包含4个训练序列，分别是A、B、C、D，其中，序列A由周期为N/4的CAZAC序列生成，序列B是序列A的共轭对称序列，C为A的反向序列，D为B的反向序列。不同天线上的训练序列通过chu序列来进行识别，假设第一个发送天线上的前导序列为c(n)，那么，第i个发送天线上的前导序列将是c(n-(i-1)·Nc/Nt」)。图5是多天线OFDM同步训练帧结构，此算法采用的天线构成，也可扩展到N×N天线序列。

图5 改进算法中的训练序列帧结构

改进算法的意义是为了使定时度量函数更加尖锐，消除传统算法中的定时平台问题，使得符号定时的精度提高，这样，可使这一帧结构能够同时实现符号同步与帧同步，同时定时算法更加简单，仅需一步便可完成。

本算法的定时度量函数采用直接利用接收信号与训练序列的相关特性来获取，这可实现尖锐的定时度量函数，帧同步算法和符号同步算法可一步完成，定时度量函数如下

其中，ci(d)表示为第i个发送天线上所传输的chu训练序列;rj(d+m)表示在第j个接收天线上d+m抽样时刻的信号。

通过上述计算，可得到获得整数频率偏移的大小估计值，通过该值，就可对帧定时位置进行补偿修正，从而获得信号在信道中传输的最强峰值位置τest，pro。

5 仿真分析

仿真参数:FFT/IFFT的变换点数为N=1 024;用户占用子载波个数N_user=1 000;插入的时域同步中导频信号做占用的点数为256;引入小数频偏因子为0.2;循环前缀长度为102;天线阵列选择2×2的天线结构;仿真次数为10 000次。

图6给出AWGN信道下信噪比为0 dB时，文中所提新算法和SC算法的归一化帧定时同步算法的定时度量函数。虚线表示SC算法的定时度量函数，直线表示新算法的定时度量函数。由图6可看出，文中所提新算法定时度量函数更尖锐且定时位置更准确。

图6 改进算法与修改过的SC算法的定时度量函数的比较

图7给出两种算法在AWGN和多径衰落信道下符号定时同步可准确检测的概率。可看出新算法相对于传统算法无论是在AWGN信道中还是在多径衰落信道中正确检测概率均更高，定时也更加准确。

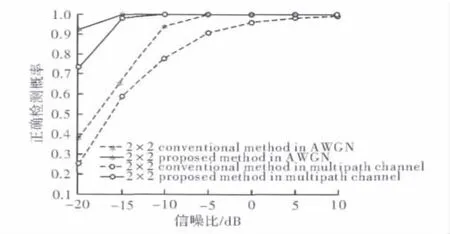
图7 符号定时估计的正确检测概率

图8为文中所提出的新算法在整数频偏存在时在AWGN信道和多径衰落信道下符号定时同步的可准确检测概率。表1给出了对应整数频偏估计的错误概率。

图8 在有整数频偏存在时，AWGN和瑞利衰落信道下定时正确检测概率曲线

表1 整数频率偏移错误检测概率

6 结束语

文中提出了一种在多径衰落信道下，基于使用chu序列生成的训练序列定时同步算法。其具有定时度量函数尖锐、定时位置准确、定时伏击正确检测概率高的优点。利用整数频偏对chu序列相关特性的影响，可直接由时域估计整数频偏，从而减少了运算量。AWGN信道和多径信道下的仿真显示了该算法的优秀性能，特别是在较低的SNR下该算法相比于SC算法更具优势。另外，由chu序列所组成的训练序列还可应用在信道估计，这使得改进的同步算法具有提高数据传输效率的潜在能力。

［1］VAN DE BEEK J J，SANDELL M，BORJESSON P O.ML estimation of time and frequency offset in OFDM systems［J］.IEEE Transactions on Signal Processing，1997，45(7):1800-1805.

［2］TIMOTHY M S，DONALD C C.Robust frequency and timing synchronization for OFDM［J］.IEEE Transactions on Communication，1997，45(12):1613-1621.

［3］MINN H，ZENG M.On timing offset estimation for OFDM systems［J］.IEEE Communication Letters，2000，4(7):242-244.

［4］BYUNG J P，HYUNSOO C.A novel timing estimation method for OFDM systems［J］.IEEE Transactions on Communication，2002，5(3):269-272.

［5］冯翀，葛万成.LTE中MIMO-OFDM的符号同步算法［J］.信息技术，2011，28(3):1-3.

［6］CHU D.Polyphase codes with good periodic correlation properties(Corresp.)［J］.IEEE Transactions on Information Theory，1972，18(4):531-532.