云制造模式下多零件的制造资源优化配置方法研究

黄 剑，刘建胜，夏芳臣

HUANG Jian，LIU Jian-sheng，XIA Fang-chen

(南昌大学 机电工程学院，南昌 330031)

0 引言

云制造是一种利用网络和制造服务平台，按用户需求组织网上制造资源（制造云），为用户提供各类按需制造服务的一种网络化制造新模式[1]。不同的地域的制造资源进行优化组合，实现短时间、低成本以及高质量的零件的加工，正是云制造资源优化配置目标。云制造资源的优化配置是实现云制造技术的关键之一[2]。目前，已有采用启发式算法研究云制造资源优化配置[2～7]。马雪芬等提出了两种可行的制造资源优化配置，以遗传算法求解制造资源优化配置模型[3]；王正成等提出了利用蚁群算法求解网络化制造跨企业资源服务链的构建问题[4]；尹胜等提出了多任务和多目标的外协加工资源优化配置模型，采用了遗传算法求解了该配置模型，并以实例验证[5]。以上已经建立了单个和多个零件的加工优化配置模型，但未对多个零件的工序选择的候选资源存在关联进行研究，这样会形成是单个零件配置的累加。针对存在的问题，本文对多个零件的工序选择候选资源存在关联情况下，提出以时间(T)和成本(C)为多目标的多零件云制造资源优化配置模型，并利用遗传算法(Genetic A1gorithm，GA)对该模型进行了求解。

1 问题描述

当企业同时存在多个零件需要同时加工，由于自身的生产能力或技术水平无法满足要求，需要求助于外部制造资源来完成零件几个或者多个工序加工。在云制造环境下，包括M个协同加工企业(包含本企业在内)，需要同时加工n个零件，每个零件j包含p道协同工序。

根据协同加工企业和零件工序情况，多个零件工序会出现选择同一候选制造资源组，因此，多个零件选择资源会存在制约关系。如图1所示，在同一工序层中，不同零件工序选择的候选资源组会出现不同或者相同。当工序选择的候选资源组不同时，不同零件工序选择的候选资源是相互独立，多个零件工序与单个零件工序选择候选加工资源是一样；当工序选择的候选资源组相同时，会出现加工等待的情况，即一个零件的一道工序加工完成后，才能加工另一个零件。这样，完成零件加工的时间包含加工时间和运输时间，还需要包含等待加工时间。

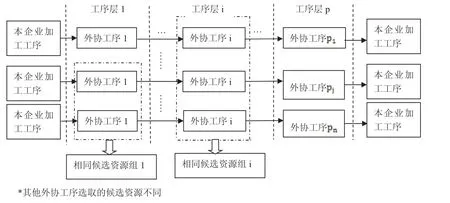
图1 多个零件工序选择候选资源存在关联示意图

云制造服务平台提供给用户的资源一定是有限的范围下，而不是无限数目。如图2所示，多个零件进行优化配置时，若同一工序层工序同时选择资源，则出现等待加工时间的情况可以分成两大类：1)n＞m时，一定要考虑等待加工时间；2)n≤m时，有两个及以上的工序选择同一资源，需要考虑等待加工时间。

图2 工序与相同候选资源组的数量关系

2 数学模型

2.1 目标函数

云制造资源的优化配置时，需要考虑包括时间、成本、质量、企业信誉及可靠性等要素。从市场需求的角度出发，本文以时间（T）和成本（C）为优化目标，并建立如下目标函数。

2.1.1 时间目标函数

当多个零件进行外协加工时，出现同一工序层的工序选择相同的制造资源组的情况下，需要考虑加工零件的等待时间。等待加工时间计算公式：

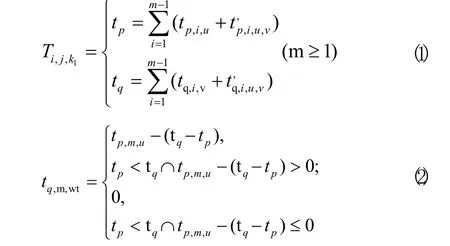
式中：tp、tq为零件p、q前m−1道工序的总加工时间(未含有等待加工时间)；tp,i,u、tq,i,v

零件i的外协工序j在候选资源u处所耗费的总时间为：

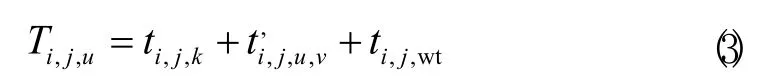
因此，其时间目标函数：

式中：n为外协加工的零件数量；mi为零件i外协加工工段数量；ri、j为零件i的工序j所对应的候选加工资源数数量；ji,j,k为决策因子，若零件i的工序j选择候选资源k，则决策变量为1，否则为0。

2.1.2 加工成本目标函数

式中： 为零件i的外协工序j在候选资源u处的加工成本；为零件i外协工序j在候选资源u与下一道工序i+1在候选资源v之间的运输成本。

2.1.3 加权求和

在云制造服务平台下，不同用户对产品的最长交货期、总成本等方面要求的侧重点不同。同时，目标函数之间既相互关联，又相互制约。通过采用最通常的权重法，将多目标转化为单目标。

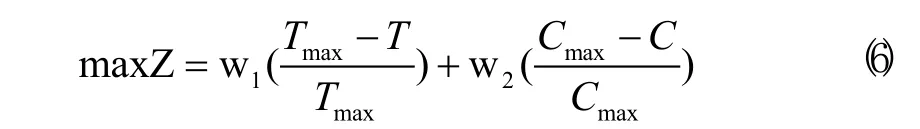
式中：w1、w2为时间、成本的权重系数，w1+w2=1；Tmax、Cmax为用户要求的最长交货期、可以支付的最高成本。

2.2 约束条件

面向多零件的云制造资源优化配置模型主要存在时间约束、成本约束和决策因子约束。

1）目标值约束

2）决策因子约束

云制造环境下，一道工序下的相同零件只能分配给一个候选资源加工，即：

3 遗传算法求解

遗传算法是一种全局性的概率搜索算法，具有对函数的性态无要求、并行性很高和搜索效率高,以及全局最优解求解能力较好等独特的性能[3]。但是，采用遗传算法对面向多零件的云制造资源优化配置模型求解，需要解决以下问题。

1）编码。 在遗传算法中，设计合适的编码方法，对于问题的表达至关重要。整数编码对于组合优化问题最为有效[8]。因此，本文采用整数编码求解。

2）最小化问题的适应度函数。 标定是将目标函数映射成适值度函数，根据不同问题，采取不同的标定方法，线性标定中的参数随着迭代次数的增加而变化时就得到了动态线性标定。动态线性标定是最常用的一种适值标定方法，计算公式是：

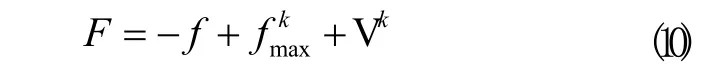
图3 选择压力的调节

3)群体规模。一般来说，遗传算法中种群规模越大越好，但是种群规模的增大也将导致运算时间的增大。假设种群规模为NP，染色体长度为1，通常情况下，1.5l ≤NP＜2l/2。

4)选择策略。Ho11and提出的轮盘赌选择是最知名的选择方式[9]。根据每个染色体的适应值的比例来确定该个体的选择概率或生存概率。若个体为i，适应值为 Fi，种群规模为NP，则该个体的选择概率为：

5)交叉概率(pc)和变异概率(pm)。 由于交叉和变异概率跟随问题的不同，可能有不的取值。对整数编码而言，交叉概率 pc=0.90～1.00，变异概率 pm=0.005～0.05，Pm＜0.05,否则，遗传算法的进化过程近似于随机搜索行为。

6)遗传算子操作。 单切点交叉是由Ho11and提出的最基础的一种交叉方式，但由于存在信息量小、末尾基因总是被交换等缺陷。在实际中大量采用两点交叉算子，本文采用双切点交叉算子。

7)修复。交叉操作和变异操作后，分别需要根据公式(7)～(9)修复个体满足约束条件。

8)终止准则。最大迭代次数作为终止准则。

4 实例

某生产企业有3个零件需要同时协同加工，其相关信息如表1、表2所示。本实例是在Visua1 Studio 2010 +SQL server2008环境下进行。 程序开始运行后，设置遗传参数：种群规模为14，最大迭代次数为100，。进行优化时，权重系数分别为w1=0.6，w2=0.4，目标值的约束为：TAmax=90、TBmax=275、TCmax=140、CAmax=850、CBmax=800、CCmax=1270。图4、图5分别是零件加工时间的读取界面和运行结果界面，其中最后获得了最优的加工路线为：0-0-0-1-0-0-1-0。对应的外协加工资源优化配置结果如表3所示。

图4 零件数据读取界面

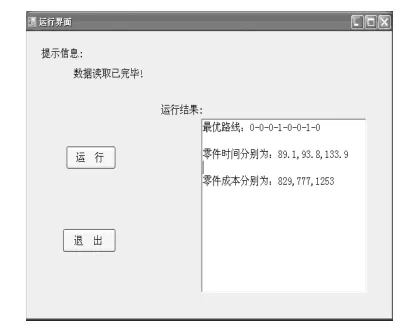
图5 程序结果界面

表1 候选资源的加工时间T、加工成本C数据

表2 候选资源之间的运输时间 t'(h)、运输成本 c'(元)

表3 最终优化配置结果

5 结论

本文探讨了多个零件的工序选择相同的候选资源时，云制造资源的优化配置问题，建立了基于时间(T)和成本(C)为目标云制造多零件制造优化配置数学模型。通过本文设计的遗传算法求解模型，并采用算例验证了模型及算法的有效性。但云制造平台环境下，用户要求的目标的优化配置不仅局限于时间和成本，因此，还需要进一步研究在云制造环境下的优化目标体系，以及多目标的优化配置模型及优化方法。

[1] 李伯虎,张霖,王时龙,等.云制造—面向服务的网络化制造新模式[J].计算机集成制造系统,2010,16(01)∶1-7+16.

[2] 王时龙,宋文艳,康玲,等.云制造环境下的制造资源优化配置研究[J].计算机集成制造系统,2012,18(7)∶1396-1405.

[3] 马雪芬,戴旭东,孙树栋.面向网络化制造的制造资源优化配置研究[J].计算机集成制造系统,2004,10(5)∶179-193.

[4] 王正成,潘晓弘,潘旭伟.基于蚁群算法的网络化制造资源服务链构建[J].计算机集成制造系统,2010,16(01)∶174-181.

[5] 尹胜,尹超,刘飞,等.多任务外协加工资源优化配置模型及遗传算法求解[J].重庆大学学报,2010,33(03)∶49-55.

[6] 刘卫宁,刘波,孙棣华.面向多任务的制造云服务组合[J].计算机集成制造系统,2013,19(01)∶199-209.

[7] 韦韫,李东波,童一飞.面向服务的网络化协同制造资源多目标重组优化调度[J].农业机械学报,2012,43(03)∶193-199.

[8] 玄光男,于歆杰.遗传算法与工程优化[M].北京∶清华大学出版社,2004.

[9] Ho11and J.Adapatation in Natura1 and Artificia1 Systems[A].Kos,Greece∶ECCOMAS,2007∶50(55)∶94-101.