约束阻尼悬臂梁阻尼特性与铺层厚度关系研究

冯 龙，邓 琼，徐亚楠

(西北工业大学 航空学院，西安710072)

随着现代科技的进步和军事的发展，军事航空系统将成为现代战争制胜的关键之一.在飞机高速飞行过程中，由于气流等因素不可避免的会产生强烈振动，这种振动不仅会造成飞机操纵稳定性下降，还可能使部分结构产生疲劳破坏，以至于结构失效［1］.针对这个问题，工程上一般通过使用阻尼材料的粘贴来控制振动的大小和频率.对于汽车，轮船等不需过多注重增重的对象，往往不会考虑阻尼贴片的质量或者厚度与减振的关系.但是对于飞机来说，每增重1克对于飞机都会造成很大的影响，所以研究阻尼贴片厚度和结构阻尼性能的关系是十分有必要的.

约束阻尼结构中的阻尼层不仅承受拉压应力，由于约束层的作用，还会承受剪切应力，这些应力会使材料内部产生拉压应变和剪切应变，从而将振动的动能转化成热能耗散掉［2］.所以约束阻尼结构是一种阻尼效率很高阻尼处理方式.因此，只要在结构或设备变形较大的部位粘贴合适的约束阻尼，就能起到减振、降噪等作用.

1 阻尼材料参数测试及拟合

1.1 阻尼层材料的DMA测试

作为约束阻尼结构核心材料的阻尼层材料，一般使用损耗因子较大的黏弹性材料，阻尼材料的损耗因子大小将直接关系到减振降噪的效果.本文中，阻尼材料使用的是北京某航天研究所研制的高分子黏弹性材料，通过DMA/861e实验机在小剪切模式下对材料进行了扫频测试，采用以1Hz为单位的线性扫频模式，范围为1～1 000 Hz.共测试3次，结果重复性良好，取3次测试平均值作为测试结果，得到图1的储存模量曲线，及图2的损耗因子曲线.

约束阻尼层处理作为最典型的一种阻尼处理方式，如图3所示.一般采用黏弹性阻尼材料作为中间层，其两面分别由弹性面层所约束.

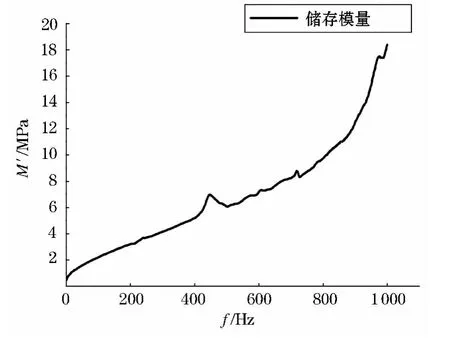
图1 阻尼材料储存模量曲

图2 阻尼材料损耗因子

图3 约束阻尼层处理示意图

1.2 阻尼层材料的Prony级数拟合

由于测试得到的是频率－损耗因子曲线，而锤击法模拟需要时域上阻尼材料的参数，参照文献［3］编写了Matlab程序对材料曲线进行了拟合，拟合结果见图4，表1.

图4 阻尼材料Prony拟合

表1 五阶Prony级数拟合结果

2 有限元软件的仿真模拟

2.1 扫频法的仿真模拟

本文使用ABAQUS软件对约束阻尼悬臂梁结构进行了模拟，结构的尺寸和参数与见表2，图5.

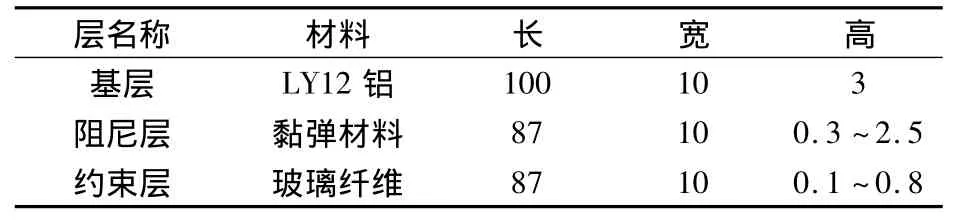
表2 约束层及阻尼层尺寸(单位:mm)

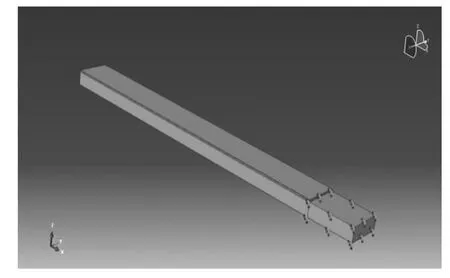
图5 悬臂梁仿真示意图

依照实体，建立如下图的模型，基层的一端采用全固支约束，约束长度为13 mm，为了满足叠层间没有发生滑移，在定义接触的时候我们用tie(绑定)类型来定义每层间的接触方式.网格按0.5的全局尺寸进行布置，采用8节点线性减缩积分单元进行划分.

分析时，先通过线性摄动分析步中的Frequency分析结构的固有频率，再由得到的固有频率来确定后续直接模态分析法中的扫频范围.根据分析，结构的固有频率在300Hz左右，故设定扫频范围为1～1 000 Hz.测试结果取悬臂梁端部的某点Z方向的幅值，取点及输出设置如图6.

图6 悬臂梁仿真网格及幅值取点图

当阻尼层厚度为0.3 mm，约束层厚度为0.1 mm时，可得到如图7的频响函数.其中纵轴为扫频测试下结构的幅值.

图7 阻尼层3 mm，约束层1 mm时频幅曲线

得到频响曲线后，通过半功率带宽法，即可以计算得到此厚度下结构的损耗因子，当阻尼层厚度为0.3 mm，约束层厚度为0.1 mm时结构的损耗因子大小为0.012 49.

依照此方法，约束层厚度按0.1 mm增长，每个约束层厚度下，阻尼层厚度按0.1 mm变化，共在扫频测试法下建立模型8×23=184个，即取得184个厚度下的结构损耗因子.按照约束层厚度不同，对所得结果进行了制图，见图8～15.纵坐标为结构损耗因子，横坐标为阻尼层厚度.

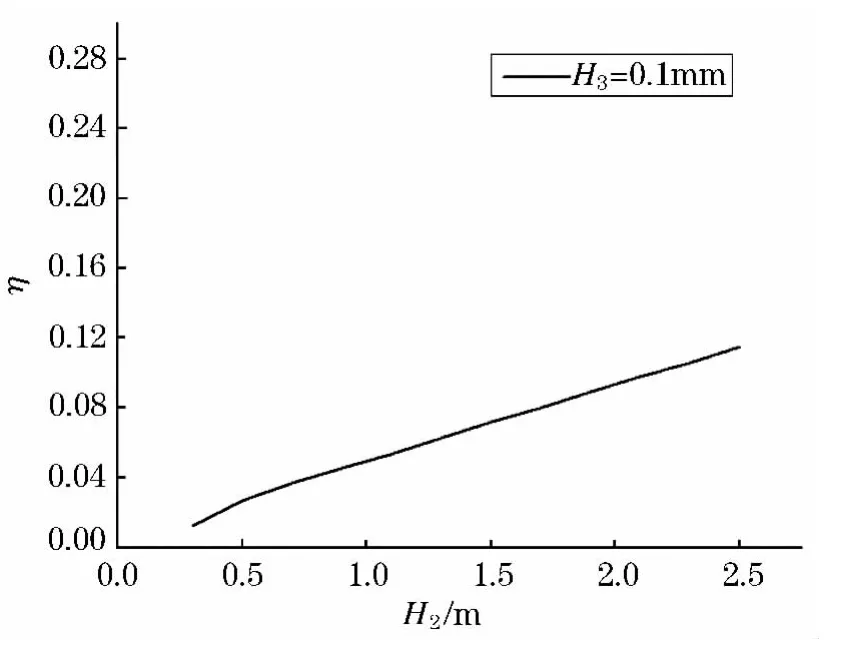
图8 约束层1 mm时损耗因子随阻尼层变化值

图9 约束层2 mm时损耗因子随阻尼层变化值

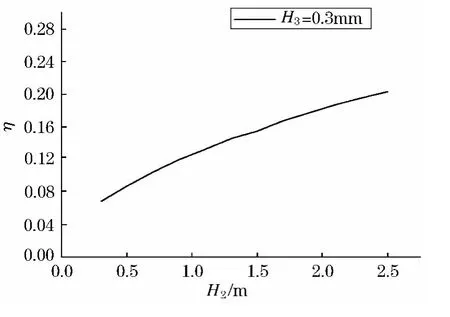
图10 约束层3 mm时损耗因子随阻尼层变化值

图11 约束层4 mm时损耗因子随阻尼层变化值

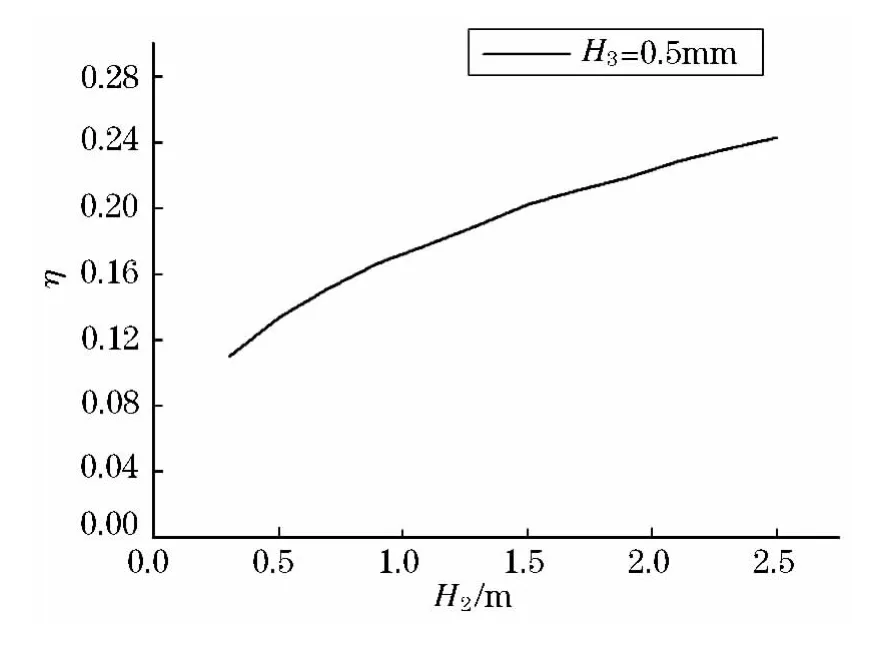
图12 约束层5 mm时损耗因子随阻尼层变化值

图13 约束层6 mm时损耗因子随阻尼层变化值

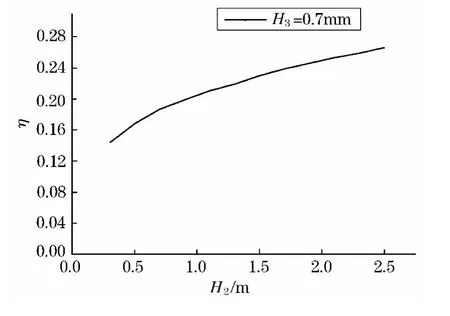
图14 约束层7 mm时损耗因子随阻尼层变化值

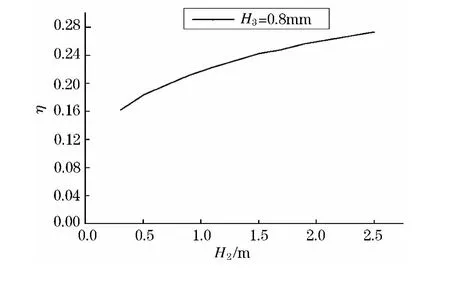
图15 约束层8 mm时损耗因子随阻尼层变化值

从图中可以看出，随着阻尼层厚度的增加，结构的损耗因子增加，随着约束层厚度的增加，结构的损耗因子也呈增长趋势.

2.2 锤击法的仿真模拟

扫频法测量的是结构的损耗因子，为了验证实验数据，本文还对锤击法进行了仿真模拟.基层、约束层的材料属性均与之前相同，阻尼层使用如图4的Prony级数5阶拟合结果，网格划分，边界条件均与扫频仿真模拟相同，使用隐式分析步，并在结构的底部距离加持端3 mm处施加一集中力，力施加的位置如图16.采用100 Hz的半正弦集中力进行加载，大小为10 N.

图16 悬臂梁锤击法施力示意图

同样，提取端部同一点的Z向位移，当H2=0.6 mm，H3=0.1 mm时，有端部位移结果见图17.

图17 阻尼层6 mm，约束层1 mm模拟衰减曲线

表3 不同厚度下结构的阻尼比

几组计算结果见表3，从表3中可以得出，随着阻尼层厚度的增加，结构的阻尼比呈增大趋势.随着约束层厚度的增加，结构的阻尼比也呈增大趋势，这与我们得到的结构损耗因子的规律相同.当损耗因子远小于1时，结构的损耗因子约等于2倍的阻尼比，可以查得，当 H2为 0.3 mm，H3为 0.1 mm时，结构2倍的阻尼比2×B1=0.01153，与之前通过扫频法测得的损耗因子误差D=0.012 49－0.011 53=0.000 96，约占锤击法结果的 8.33%，由于振动的复杂性，这个结果是可以接受的.

将其余厚度阻尼比阻计算结果的2倍与损耗因子曲线比较，差别均小于5%.

3 锤击法实验

为了约束层采用威海光威复合材料有限公司生产的G12500号玻璃纤维预浸料，基层为LY12铝，结构如图18.

图18 实验用悬臂梁结构示意图

表4 实验结构尺寸(单位:mm)

图19 约束阻尼悬臂梁实验测试装置图

测试设备采用西北工业大学固体力学振动实验室的测试设备，将悬臂梁加持在振动台上，采用全固支模式.具体结构参数见表4.其中，约束段长度13 mm，自由端87 mm，使用激励锤在根部的敲击提供所需要的脉冲信号，并采用红外位移传感器收集悬臂梁端部的位移衰减信号，具体实验设备如图19.

测试结果见图20，从图20中可以清楚的看到结构端部位移的衰减情况.

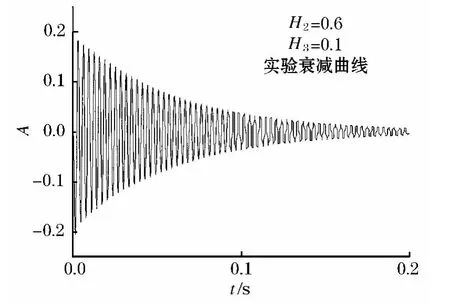
图20 阻尼层6 mm，约束层1 mm实验衰减曲线

由于结构设计的刚度较大，故衰减较快，振动幅值较小，通过对数衰减率法对实验结果进行处理，可以得到当阻尼层厚度为0.6，约束层厚度为0.1 时，结构的阻尼比为 0.011 98，与仿真解 0.012 615的误差 D'=0.012 615 －0.011 08=0.000 635，约占实验值的5.30%.同样，对于振动这样一个复杂的过程，这样的结果是十分理想的，从而证明了锤击法仿真的正确性，同时也证明了约束阻尼结构损耗因子的准确性［4－6］.

4 结语

通过扫频测试的ABAQUS仿真模拟，得到了当基层为3 mm时，不同厚度阻尼层厚和约束层的约束阻尼悬臂梁结构损耗因子值.当阻尼层和约束层的厚度增加时，结构的损耗因子也增加.对不同阻尼层和约束层的悬臂梁结构进行了锤击法的ABAQUS有限元模拟，结果表明，锤击法与扫频法测试结构损耗因子的数值模拟误差很小，均在10%以内，因此两种方法可以在一定条件下等效.并且，随着阻尼层和约束层厚度的增加，结构的阻尼比增加.对约束阻尼结构进行了实验测试，结果表明，当基层为3 mm，阻尼层厚度为0.6 mm，约束层厚度为0.1 mm时，实验测得的结构阻尼比与锤击法模拟的结构阻尼比误差仅为5.30%.因此验证了锤击法模拟的正确性，从而也可以说明结构损耗因子的正确性.

［1］龚庆祥，施荣明，屈见忠.航空振动故障实例分析汇编［M］.北京:航空工业出版社，1995.

［2］戴德沛.阻尼减振降噪技术［M］.西安:西安交通大学出版社，1986:88－89.

［3］SLANK M.A numerical and experimental investigation of steel beams damped with constrained viscoelastic layers［M］.Montreal:McGill University，1998.

［4］郭红锋，黄友剑，李 鹏，等.基于FEA技术的E型钢阻尼器优化设计.科学技术与工程，2012，12(5):1191－1194.

［5］姚千斌.金属材料阻尼测试研究［D］.西安:西北工业大学，2007.

［6］余建新，陈立平.复合材料结构阻尼测试分析［J］.哈尔滨商业大学学报:自然科学版，2011，27(5):729－732.