求解非线性不适定算子方程的一种Landweber迭代法

王美吉，潘状元

(哈尔滨理工大学应用科学学院，哈尔滨150080)

1 引言

考虑非线性算子方程

其中:F:D(F)⊂X→Y，X，Y为 Hilbert空间.F是Frechet可微.

这里考虑算子方程的解不连续依赖于右端数据的情况.由于不稳定性并且在实际问题中只有近似数据yδ满足

这里为测量误差δ＞0的界.

对于此类非线性问题的解法，一般通过正则化方法来得到其解的近似.由于非线性不适定问题在生活中的广泛应用，已经成为横跨应用数学和计算

数学两个学科的真正的研究领域［1］.其理论研究大致有以下几个方面如 Tikhonov正则化方法，最大嫡方法，有限维逼近等［2－5］.对于非线性问题人们对Landweber迭代法给予了很大关注，文献［5］证明了Frogen Landweber迭代法的收敛性并进行了数值试验.

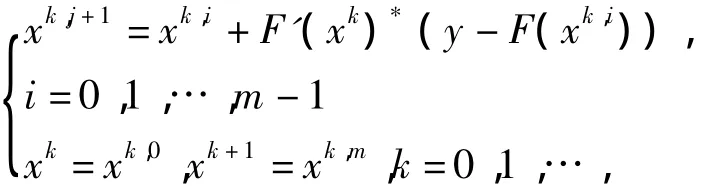
由于在实际问题中，算子一般也是经测量而获得的近似值，或是由离散过程而得到的原算子的一个有限维的逼近，因此真正要求解的是式(1)的一个近似方程

其中:h表示Fh逼近F的程度，假定满足

因此，在考虑Landweber迭代时，也应考虑算子亦有扰动的情况.

假定扰动算子Fh仍保持算子F的Frechet可微且F'h在D(F)上一致收敛于F'(当h→0)，本文在前人研究成果基础上提出了非线性算子方程算子与右端皆有扰动的Landweber迭代法.迭代格式为

按广义误差准则

来确定迭代终止步k*，则迭代序列{xδhk*}收敛到

不失一般性，假定

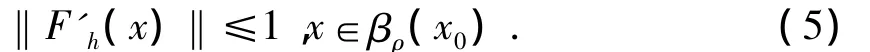
其中:βρ(x0)为以x0为中心，ρ＞0的开球.

2 单调性分析

对于上述迭代格式，本文以m=2为例，理论验证此迭代格式的收敛性.则此迭代带格式可以改写成引理1［6］如果式(3)成立，x*是方程(1)在 βρ(x0)中的一个解，那么任意解∈βρ(x0)满足，，反之亦然，N(·)表示算子的核空间.

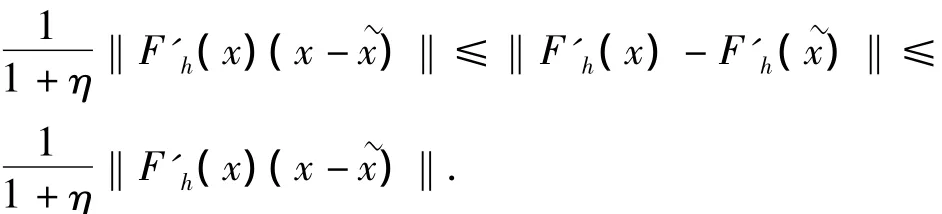
引理 2［7－8］假设 x*为式(1)在 βρ(x0)中的一个解，对于扰动数据满足‖yδ－y‖≤δ，k*是按广义误差准则(4)所确定的迭代终止步.若条件(3)、(5)成立，则有

当δ=h=0时

证明:由引理2知，

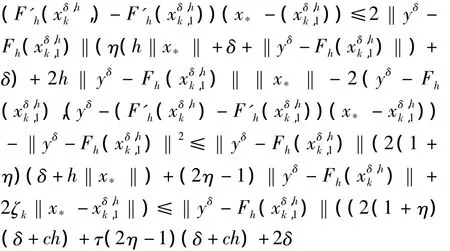
由式(4)和假设条件有

证明方法见文献［5］.

3 收敛性分析

定理2 如果在Bρ/2(x*)中满足式(3)、(5)，算子方程(1)可解，则xk收敛到式(1)的一个解x*∈Bρ/2(x*).若x+是离x0最近的惟一解，且N(F'(x+))⊂(F'(x))，成立，则xk收敛到x+.

证明:令ek:x*－xk

由定理1知{‖ek‖}单调下降，下界为某ε≥0，下证{ek}是 Cauchy 列.对 j≥k，取 l(j≥l≥k)使成立

由三角不等式，有

下证明(el－ek，el)也收敛到零(当k→∞时)改写

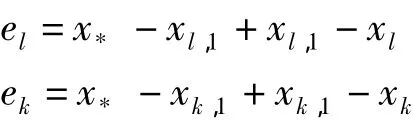
由引理 2 推知，当 k，l→∞ 时 xl，1－ xl，xk，1－ xk趋于零.令

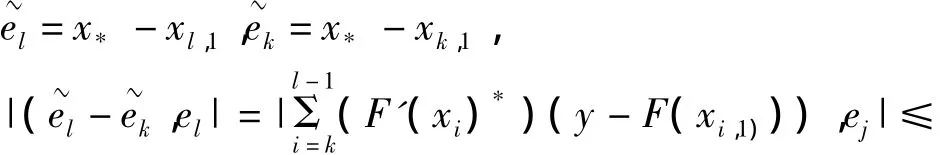
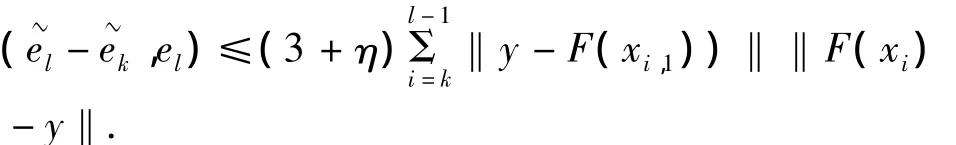
由此得{ek}为 Cauchy列，所以{xk}也为Cauchy列.设 xk→x*，又因为 F(xk)→y(k→∞)，从而x*为式(1)的解.若式(1)有惟一的距x0最近的解，则x+满足

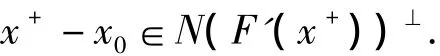
对任何 k=0，1，2，…若，N(F'(x+))⊂N(F'(xk))，则有

证毕.

定理3 在定理2的前提条件下，方程(1)可解，取h=0，扰动终止于K*(δ).那么当 δ→0时，收敛到式(1)的解.

证明参见文献［5］中命题3.

定理4 假设条件(3)(5)成立，方程(1)可解，则当 h→0，δ→0 时，xδhk*收敛到(1)的解.

用归纳法易证，上式第一项当h→0时趋于零，而由定理3，第二项当δ→0时也是趋于零的，从而

4 结语

针对非线性不适定问题的求解，本文首先从Frozen Landweber迭代法入手，提出非线性算子和右端数据皆有扰动的Landweber迭代法.并且对所提出的迭代格式给出了收敛性证明.从理论分析可以看出，Frozen Landweber迭代法确实是求解非线性不适定算子方程的一种简单而稳定的方法，适合于处理算子与右端数据皆有扰动的实际问题，并且避开了Tikhonov正则化方法正则参数选取困难以及传统的Langweber迭代法收敛太慢的问题.不足之处是没有对此迭代格式进行数值试验，这将是下一步进行的工作.

［1］DENG Y J，LIU Z H.New fast iteration for determining surface temperature and heat flux of general sideways parabolic equation［J］.Nonlinear Anal.Real World Appl.，2011，12(1):156 －166.

［2］ZHENG G H，WEI T.Two regularization methods for solving a Riesz－Feller space－frational backward diffusion problem［J］.Inverse Problems，2010，26:1 －22.

［3］JIN Q N.On a regularized Levenberg－Marquardt method for solving nonlinear inverse problems［J］.Numer.Math.，2010.115:229－259.

［4］YANGQQ，LIU F W，TURNER I.Numerical methods for fraction partial differential equations with Riesz space fractional derivatives［J］.Appl Math Model.，2010，34:200 －218.

［5］XU J，HAN B，LI L.Frozen Landweber Iteration for Nonlinear Ill－ Posed problems［J］.Acta Mathematicae Applicatae Sinica，2007，23(2):329 －336.

［6］HANKE M.Accelerated Landweber Iterations for the Solution of Ill－ Posed Equations［J］.Numer.Math，1991，60(1):341 －373.

［7］韩 波，刘家琦，后步风.非线性不适定算子方程算子与右端项皆有扰动的 Land weber迭代法［J］.计算数学，2002，24(4):479－486.

［8］皮丽敏，潘状元.一族求解非线性方程的高阶迭代方法［J］.哈尔滨商业大学学报:自然科学版，2012，28(6):751－753，768.