动态散列目录扩展算法的研究

陈慧杰，李建伟

（太原科技大学计算机科学与技术学院，太原 030024）

散列是一种广泛应用在数据检索领域的索引机制。动态散列是指随着数据量的增减，散列的目录长度可以相应伸缩的散列。其主要由目录、散列函数、目录扩展方法组成，散列函数对记录的关键字进行处理可以得到记录在目录中的对应位置，目录提供了目录项与地址的映射关系，目录扩展方法是目录伸缩的策略［1］。

在各种动态散列模型中，线性散列［2］和动态散列［3］是两种比较经典的动态散列算法，其不同主要体现在每次桶分裂所导致的目录增长数目。前者每次分裂都会导致一个目录单位的增加，而后者并不是每次桶分裂，目录长度都会改变，但是目录长度在需要增长的时候必须增长一倍。还有一种改进后的动态散列［4］，根据分裂桶属性的不同，目录增长单位可以是1个到一倍多种情况。

影响动态散列目录增长的因素主要为分裂条件与数据偏斜性两方面。分裂条件一般有桶溢出与存储利用率两种。数据偏斜性主要有数据集中分布于目录的前端、中端和后端三种情况。本文将从分裂条件和数据偏斜性两方面对上述三种动态散列的目录增长的影响进行研究。

1 动态散列目录扩展方法

1.1 线性散列

线性散列最早由Larson提出，其分裂的方法概述如下:假设散列表目录当前状态包含N个位置，位置标记为0、1、2……N-1.定义一个阶数 i，与当前状态的目录长度N的关系为2i＜N≤2i+1.则在需要分裂的情况下将被分裂的桶号为N%2i.将该桶中数据的关键字对2i+1求余，将余值等于N%2i+1的数据放置目录号为N%2i+1所指向的桶中。

由上可知，线性散列每次桶分裂只扩展一个目录位置，可有效避免目录的激增，但是由于待分裂的桶不是记录所插入的溢出桶而是由当前目录长度决定，所以无论分裂触发条件为溢出分裂还是存储率上限分裂，都会产生大量的溢出桶。

1.2 可扩展散列

可扩展散列由Fagin提出，在结构上，与线性散列不同之处在于引入了目录，目录项指向对应的数据桶。分裂时，可使目录的增长代替桶的分裂，来实现溢出桶可以立即分裂的目的。另外，可扩展散列中提出了全局深度和局部深度的概念，全局深度Gd与散列当前目录项长度N的关系为N=2Gd.每个数据桶都有各自的局部深度Bd，其与该桶中数据关键字Key和目录项号Index_id的关系为:

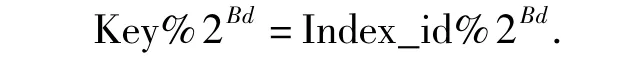
Gd与Bd的关系为Gd≥Bd.当Gd＞Bd时，至少有两个目录项指向同一个数据桶。该桶为共享桶，指向共享桶的目录项为兄弟目录项。

分裂方法［5］概述如下:当分裂条件满足后，判定待分裂桶的局部深度Bd与全局深度Gd的关系，当Bd＜Gd时，不需要目录扩展操作，仅需完成桶分裂及相应操作即可。当Bd==Gd时，目录项需要扩展一倍，即扩展后目录项数为2N，全局深度Gd自加一。将新产生的N个目录项分别指向对应的共享桶，然后完成桶分裂及相应操作即可。如果在数据具有一定偏斜度的情况下，目录项的目录会骤增，从而致使内存浪费。

1.3 改进后的动态散列

该散列的设计目的是设计一种溢出桶可以及时分裂并且目录扩展速度较慢的动态散列。散列结构由具有全局深度的目录和具有局部深度的数据桶组成。假设散列表目录当前状态包含N个位置，位置标记为0、1、2……N-1.待分裂数据桶的目录项号为:split_b=key%（1＜＜Gd）（“＜＜”意为逻辑左移）。待分离数据桶的兄弟目录项为:Max_b=split_b+（1＜ ＜Gd）.

如果分裂条件满足，根据待分裂桶的局部深度Bd与全局深度Gd的关系进行如下操作:

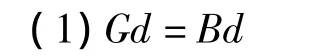
将目录项数从N扩展至Max_b.新扩展的目录指向各自的兄弟桶。为Max_b分配一个空数据桶。将待分裂数据桶中模1＜＜（Gd+1）等于Max_b的数据加入到Max_b的数据桶中。Gd自增1.split_b和Max_b执行数据桶的局部深度等于split_b指向的数据桶的局部深度增1.

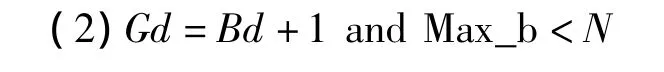
为Max_b分配一个空数据桶。将待分裂数据桶中模1＜＜（Gd+1）等于Max_b的数据加入到Max_b的数据桶中。

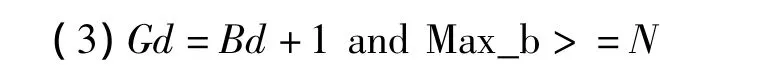
扩展当前目录项数从N至Max_b.新扩展的目录指向各自的兄弟桶。为Max_b分配一个空数据桶。将待分裂数据桶中模1＜＜（Gd+1）等于Max_b的数据加入到Max_b的数据桶中。

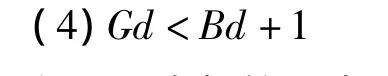
记录所在桶的最小目录项Mini_b=key%（1＜＜Bd）.最小目录的最接近的兄弟目录项为:bro_Mini_b=key%（1＜＜Bd）+（1＜＜Bd）.为bro_Mini_b分配一个空数据桶。将待分裂数据桶中模1＜＜（Bd+1）等于bro_Mini_b的数据加入到bro_Mini_b的数据桶中。将Mini_b和bro_Mini_b在目录中的目录项指向各自的数据桶。

2 实验与分析

2.1 分裂条件对目录尺寸的影响

分裂条件一般分为桶溢出［6-7］与存储利用率［8-9］。桶溢出是被插入记录所在桶的数据量大于其容量。存储利用率的计算如公式（1）。其中SRate为存储利用率，recordNum为记录总量，index-Num为目录项数目，bucketCapacity为数据桶容量。在线性散列中，目录项数目为实际数据桶的数目。

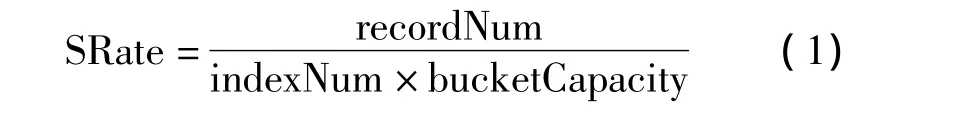
采用随机生成数据作为实验数据，数据桶容量bucketCapacity=30，存储利用率上限为 SRate=0.75.设定在可扩展散列和改进的动态散列中，当分裂条件为桶溢出时，待分裂桶为当前溢出桶，当分裂条件为存储利用率时，待分裂桶为容纳数据量最多的桶。在数据分布比较均匀的情况下，分别采用存储利用率和桶溢出作为分裂条件，对三种动态散列进行实验。实验结果如图1～图3所示。图中虚线代表采用存储利用率作为分裂条件，实线代表采用桶溢出作为分裂条件。

由图1～图3可知，对于线性散列、可扩展散列、改进后的动态散列，随着数据量的增长，采用桶溢出分裂与采用存储利用率分裂相比，目录增长速度较快，溢出桶数目较少。

2.2 数据偏斜性对目录尺寸的影响

由于在在实验过程中，目录长度N是会变化的。所以设定数据的在目录中前端、中端和后端的三种分布为对0号、N/2号、N-1号目录项进行数据插入。数据桶容量bucketCapacity=30.存储利用率上限为SRate=0.75.实验数据总数量为300.

实验结果如表1.

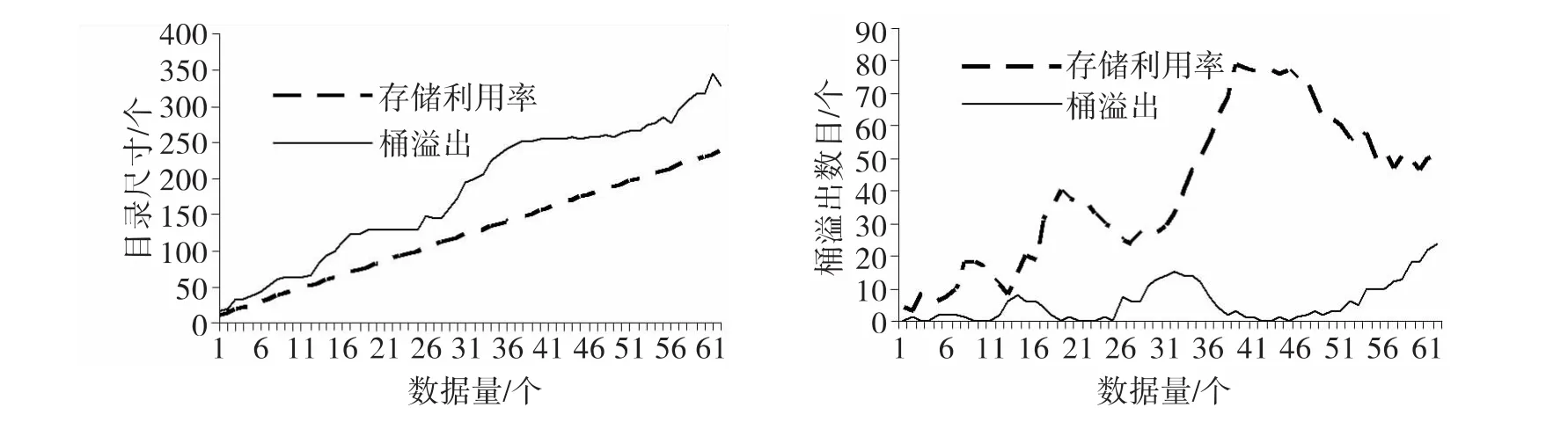
图1 随数据量增长线性散列的目录尺寸和桶溢出数增长趋势图Fig.1 The trend graph of index size and overflow bucket number of linear hash with the increasing data

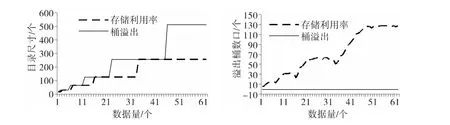
图2 随数据量增长可扩展散列的目录尺寸和桶溢出数增长趋势图Fig.2 The trend graph of index size and overflow bucket number of extendible hash with the increasing data

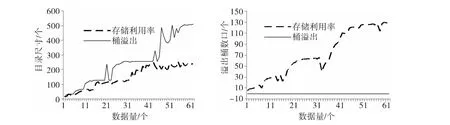
图3 随数据量增长改进的动态散列的目录尺寸和桶溢出数增长趋势图Fig.3 The trend graph of index size and overflow bucket number of the improved dynamic hash with the data increasing

表1 三种动态散列在数据偏斜情况下目录尺寸数据Tab.1 the data of index size of the three dynamic hashes with data skew

纵向比较表1中数据可知:采用存储利用率作为分裂条件时，数据集中分布于目录的前端、中端和后端的三种数据偏斜性对线性散列和可扩展散列的目录增长的影响相同。采用桶溢出作为分裂条件时，对于线性散列，数据分布越靠后端，目录增长越慢。对于改进的动态散列，目录增长越慢。

横向比较表1中数据可知。数据集中分布于目录的前端、中端和后端的三种数据偏斜性对改进的动态散列的最糟糕条件下的影响与对可扩展散列的影响相同，最优条件下的影响与对于对线性散列的影响相同。

3 结论

本文针对桶溢出、存储利用率两种分裂条件和数据分布于目录前端、中端、后端三种偏斜性分布对线性散列、可扩展散列、改进的动态散列的目录尺寸扩展的影响进行了研究。通过实验，结果表明，随着数量的增长，采用桶溢出分裂与采用存储利用率分裂相比，目录增长速度较快，溢出桶数目较少。在数据具有偏斜性的情况下，采用存储利用率作为分裂条件时，三种数据偏斜性分布对线性散列和可扩展散列的目录增长情况相同。采用桶溢出情况时，对于线性散列，数据分布越靠后端，目录增长越慢。对于改进的动态散列，数据分布越靠后端，目录增长越快。

［1］RAMMOHANRAO K，LIOYD JOHN W.Dynamic Hashing Schemes［J］.Computer Journal，1982，25（4）:475-485.

［2］LITWIN W.Linear hashing:a new tool for file and table addressing［C］∥Proceedings of the 6th international conference on very large data bases.Canada:Montreal，1980:212-223.

［3］FAGIN R，NIEVERGELT J.Extendible hashing-a fast access method for dynamic files［J］.ACM Trans Database Syst，1979，4（3）:315-344.

［4］CHEN HUIJIE，LI JIANWEI.The Research of Embedded Database Hybrid Indexing Mechanism Based on Dynamic Hashing［C］∥Proceedings of the 2012 International Conference on Information Technology and Software Engineering.Germany:Springer Berlin Heidelberg，2013:691-697.

［5］LI XIANG，ZHOU D，MENG X F.A New Dynamic Hash Index for Flash-Based Storage［C］∥Proceedings of the 9rd Conference on Web-Age Information Management.Washington:IEEE Computer Society，2008:93-98.

［6］RATHI A，LU H.Performance comparison of extendible hashing and linear hashing techniques［C］∥Proceedings of the 1990 ACM SIGSMALL/PC Symposium on Small Systems.New York:ACM，1991:19-26.

［7］LARSON P.Performance analysis of a single-file version of linear hashing［J］.Computer Journal，1985，28:319-326.

［8］YANG CHUL-WOONG，LEE KI-YONG，KIM HO，et al.An Efficient Dynamic Hash Index Structure for NAND Flash Memory［J］.IEICE TRANSACTIONS on Fundamentals of Electronics，Communications and Computer Sciences，2009，E92-A7，1716-1719.

［9］YOO MIN-HEE，KIM BBO-KYEONG，LEE DONG-HO.Hybrid Hash Index for NAND Flash Memory-based Storage Systems［C］∥Proceedings of the 6th International Conference on Ubiquitous Information Management and Communication，USA:NY，2012.