双轴跟踪光伏阵列的日地天文理论仿真实现

刘立群，田 行，葛 竹，曹 伟

(太原科技大学电子信息工程学院，太原 030024)

随着环境问题在世界范围内的日益严重，世界各国越来越重视开发和利用可再生能源。在所有的可再生能源当中，太阳能的储量最为丰富，太阳能的热利用和太阳能光伏发电在未来的能源结构中必将占据重要的地位，而提高昂贵的光伏发电系统和太阳能集热系统的输出效率是太阳能学界迫切需要解决的重要问题，也是实现未来低碳社会的基本要求。[1]

目前，许多国家已建成了一些大型的光伏发电项目，而国内外大多数PV阵列大多以一定倾角固定于地面，因此太阳光入射角与PV板表面法线间存在一定的角度差，导致PV板不能充分吸收太阳辐射能，因此单轴或双轴跟踪系统被一些专家用来实现对太阳高度角和方位角的实时跟踪。然而，目前存在的方法大多是固定PV板的跟踪速度和跟踪角度，并没有考虑实际的维度、日出角、日落角和高度角等日地信息，导致跟踪角度与实际角度间存在较大误差，使得PV发电系统输出效率降低。本文将针对已经确定的纬度，通过日地天文分析得到一年、一月和一天中太阳运行的高度角、方位角、日出角、日落角、日照时间等数据，进而对比PV板在固定角度和双轴跟踪情况下输出效率，说明双轴跟踪对于昂贵的光伏阵列的必要性。

1 基础知识

太阳的直径约为地球直径的109.3倍，达到1.39 ×106km，释放出的能量达到3.865 ×1026J/s，其中大约有(1/22)×10－8km太阳辐射能通过约1.5 ×108km 的距离到达地球，即 1.73 ×1017W/s，而能够到达地球表面的太阳辐射能约占51%，其余的被大气吸收(约占19%)或被大气、尘粒和地面反射回宇宙空间(约占30%)。

地球绕地轴自西向东旋转，称为自转，自转一周约为24 h，同时地球绕太阳以椭圆形轨道运行，称为公转，公转一周为1 y，其中椭圆形轨道称为黄道。在日地运动过程中，地球的自转轴与黄道面的法线倾斜夹角为23.45°，同时由于地球公转时的自转轴始终指向地球的北极，导致太阳光线直射地球表面的位置时而偏南，时而偏北，形成了地球上的四季变化[1-5]。

2 天文参数及太阳辐射

2.1 日地距离

太阳与地球间的距离约为1.5×108km，但地球绕太阳的运行轨道是椭圆形的，因此必然存在近地点(发生在每年的1月1日，日地距离约为1.471×108km)和远地点(发生在每年的7月1日，日地距离为1.521×108km)。即每天的日地距离都是变化的，Spencer在1971年提出的地球轨道偏心修正系数为:

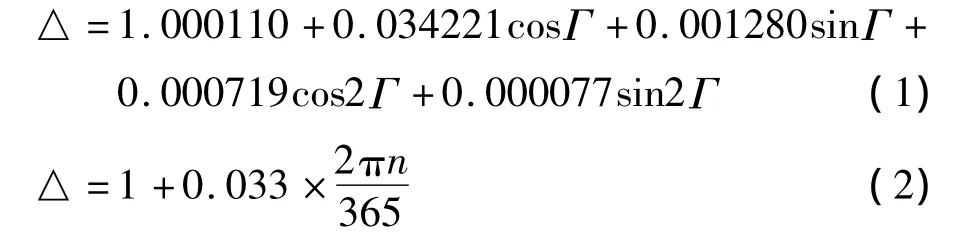
在实际的工程中，式(1)可以用式(2)简便计算，其中，Γ为一年中某一天的角度，即日角，可按照式(3)计算，其中 n为一年中某一天的顺序数[1-2]。

2.2 时角

在天球系统中，认为太阳是绕地球旋转，即太阳每天的东升西落，称为太阳视旋转。每天的视旋转用时角ω表示，并设太阳正午时角为0，上午时角为负，下午时角为正。由于地球自转一周为360°，因此1 h的太阳视旋转为15°.某整点时刻的时角可表示为式(4)，其中 T ∈[1，24][1-2].

但由于地球绕太阳的轨道为椭圆形，而钟表时间(平均太阳时间)是以假定地球绕太阳的轨道为圆形得到的，所以实际太阳时间ts与平均太阳时间之间t存在时差e，其中ts可以表示为式(5)，e可以近似表示为式(6)。

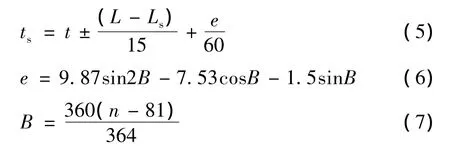
其中，L为当地的地理经度;Ls为当地地区标准时间位置的地理经度，式中的 ±号，东半球取正，西半球取负。

2.3 赤纬角

地球赤道平面与地球中心和太阳中心连线的夹角，称为赤纬角δ，其中在春分日(北半球3月20/21日)和秋分日(北半球9月22/23日)δ=0°，夏至日(北半球6月21/22日)δ=23.45°，冬至日(北半球12月21/22日)δ= －23.45°.δ的精确计算可以由式(8)或式(9)得到，而在实际工程中可采用Cooper提出的式(10)或Brichambaut提出的式(11)进行 δ的简便计算[1-2]。

式(8)中，N1=92.957，N2=93.629，N3=89.865，N4=89.012，α1为从春分日开始计算的天数，α2为从夏至日开始计算的天数，α3为从秋分日开始计算的天数，α4为从冬至日开始计算的天数。

2.4 天顶角θz、高度角αs和方位角γs

图1显示了天顶角、高度角和方位角间的地平坐标系，其中天顶角就是太阳光线与地平面法线间的夹角;高度角是太阳光线和它在地平面上投影线间的夹角;方位角是太阳光线在地平面上投影线和地平面正南方向线之间的夹角，计算时以正南方向为起点(即0°)，顺时针方向(向西)为正，逆时针方向(向东)为负。其中天顶角与高度角满足式(12)[1-2]。

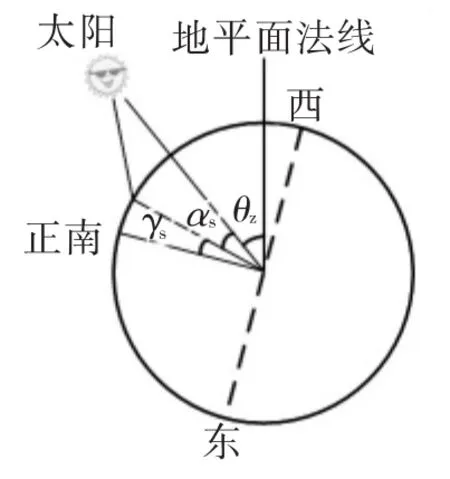
图1 地平坐标系[1]Fig.1 Coordinates of horizontal system

高度角、天顶角与纬度、赤纬角和时角间的关系可表示为:

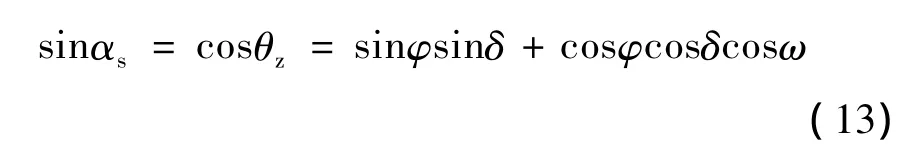
方位角与高度角、纬度、赤纬角和时角间的关系可表示为:

2.5 日出时角ωsr、日落时角ωss和日照时间N

每天日出和日落时的太阳高度角等于0，根据日出、日落时的时角 ωs=arccos(－ tanφtanδ)，可得:

则全天的日照时间可表示为:

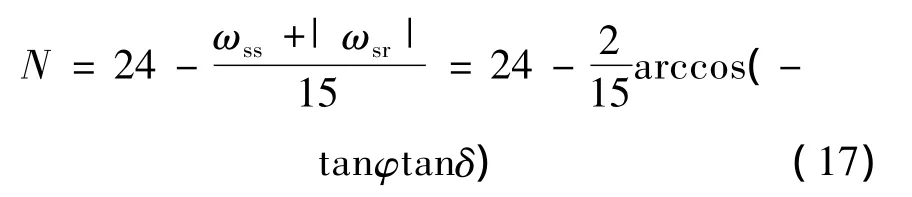
2.6 日出日落的方位角 γs，0

每天日出日落时太阳的方位角都是不同的，γs，0与赤纬角、纬度的关系如式(17)所示:

根据式(17)得到的日出日落时的方位角都有两组解，但由于我国位于纬度为0～66.55°的北半球，因此在夏半年(赤纬角 ＞0)，日出日落都位于数学坐标系的第一、二象限，在冬半年(赤纬角 ＜0)，日出日落都位于数学坐标系的第三、四象限。

2.7 到达地表的法向太阳直射辐射度

到达地表的法向太阳直射辐射度可以表示为式(18)，其中Is是太阳常数，根据1981年世界气象组织仪器和观察方法委员会第八届会议通过的太阳常数值为1367±7 W/m2为修正m=2时的值Pm，Pm表示大气对太阳辐射的衰减程度，可由式(19)得到;太阳与天顶轴重合时，太阳光线穿过地球大气层的路程最短，m表示太阳光线经过的实际路程与此最短路程之比称为大气质量，可由式(20)或式(21)得到。

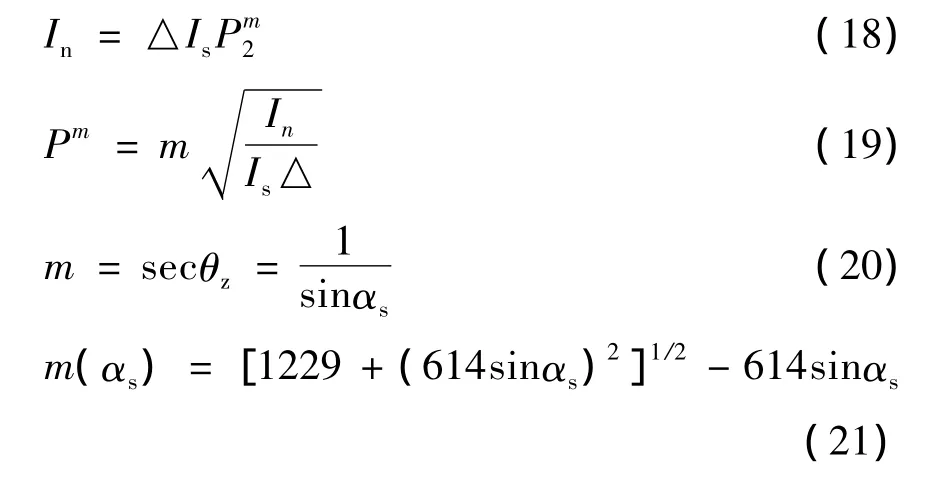
3 仿真分析

通过前述分析可知，到达地球的太阳光线受到太阳常数、大气质量和天顶角等因素的影响，对于地球上的某一点光伏阵列而言，则到达光伏表面的太阳辐射强度与纬度、太阳高度角、方位角、赤纬角等日地天文参数有关。

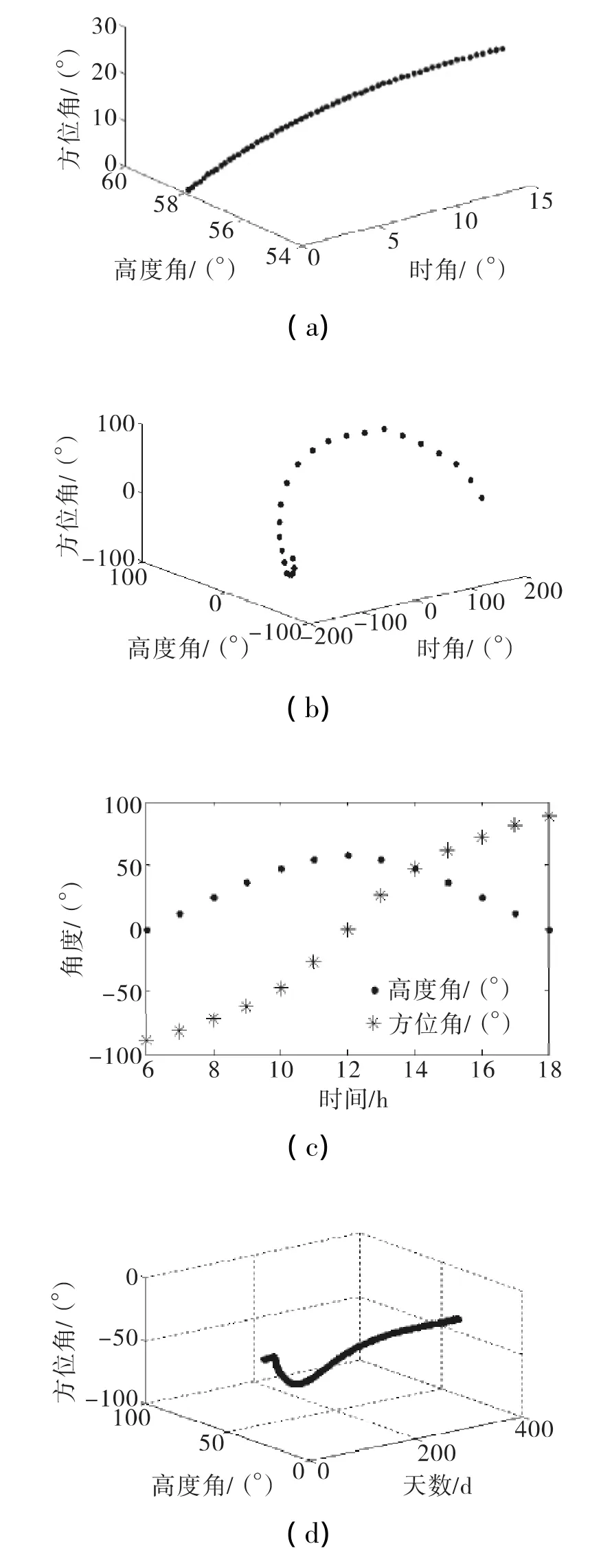
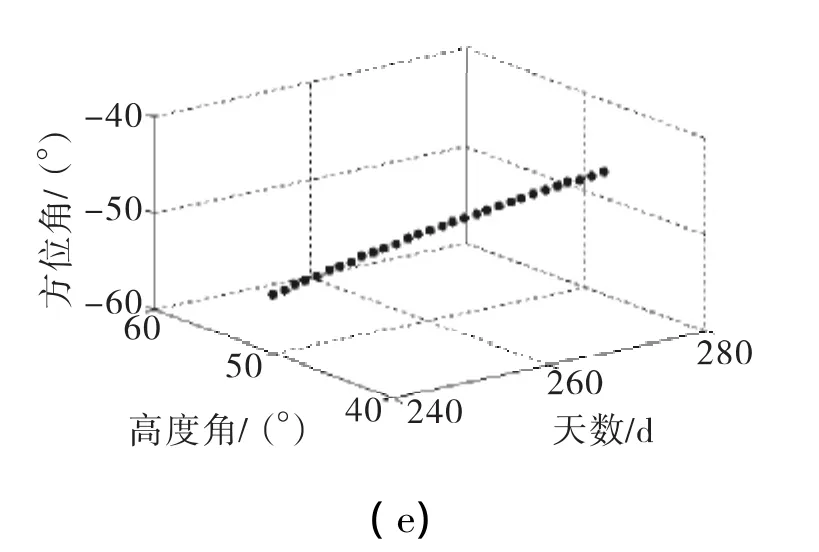
图2 太阳高度角和方位角变化Fig.2 Changes of the solar elevation angle and azimuth angle

图2显示了太阳高度角和方位角在不同时间范围内的变化，图2(a)显示的是秋分日(9月22/23日)1 h内(中午12时至1时)的变化;图2(b)显示了秋分日1 d内的变化;图2(c)显示了秋分日从日出到日落的变化;图2(d)显示了全年每天上午10时的变化;图2(e)显示了9月份每天上午10时的变化。其中文中以上海的纬度为例，在Matlab R2010a仿真环境下，构建太阳运行方位数学模型，进而可以获得不同时间和地点的太阳运行位置。由图可知，太阳的高度角和方位角时刻都在变化，即每分钟、每天、每月都在变化，因此如果在地球表面上的某一位置采用固定倾角安装的光伏阵列，必将导致该阵列的高度角和方位角只有某一时刻可以达到最佳，而其它时刻都将偏离最佳的高度角和方位角，进而降低阵列的输出效率。因此对于光伏阵列而言，太阳的双轴跟踪是必须的。

4 结论

通过对太阳和地球天文参数的分析，利用Matlab软件仿真出不同时间范围内的太阳高度角和方位角变化，发现传统的固定倾角的光伏阵列无法时刻对应最佳的太阳高度角和方位角，当然也无法接收到最大的太阳辐射度，即无太阳双轴跟踪控制的光伏阵列的输出效率将非常有限。

[1]杨金焕，于化丛，葛亮.太阳能光伏发电应用技术[M].北京:电子工业出版社，2009.

[2]刘鉴民.太阳能利用原理、技术、工程[M].北京:电子工业出版社，2010.

[3]SALAH A，SALEM N.Two axes sun tracking system with PLC control[J].Energy Conversion and Management 2004，45(11-12):1931-1939.

[4]CEMIL S.Multi-axes sun-tracking system with PLC control for photovoltaic panels in Turkey，Renewable Energy [J].2009，34(4):1119-1125.

[5]HOSSEIN M，ALIREZA K J，ARZHANG M，et al.A review of principle and sun-tracking methods for maximizing solar systems output[J].Renewable and Sustainable Energy Reviews，2009，13(8):1800-1818.