浓缩机设计理论分析及应用

赵 鑫，郭亚兵

(太原科技大学环境与安全学院，太原 030024)

重力浓缩机是工业固液分离的重要设备之一。浓缩机的工艺性能取决于被处理的固体物料的物理性能及化学性能[1]。浓缩机可以通过现有的浓缩机的运行参数、经验数据、小型的连续沉降实验及间断沉降试验来进行选型设计。最实用、最经济的方法是间断沉降试验，但需要沉降理论对实验数据进行处理，得到不同底流浓度时的固体负荷，对浓缩机进行选型。近几十年来，沉降浓缩理论有了快速发展，浓缩机选型设计理论日趋完善。目前，浓缩机设计理论主要分三种类型:第一是基于物料微平衡的设计理论，设计方法包括了Mishler法和Coe-Clevenger法;第二是基于运动学沉降过程的设计理论，运动学设计理论又可分为静态Kynch沉降过程理论和连续 Kynch沉降过程理论[2]，静态Kynch沉降过程理论包括了 Kynch法、Talmage-Fitch法和Oltman法，连续Kynch沉降过程理论包括了Yoshioka-Hassett法和 Wilhelm-Naide法;第三是基于动力沉降过程的设计理论，包括絮凝悬浮液理想连续浓缩过程模型和Adorjan法。在这些方法中，Talmage-Fitch法和Wilhelm-Naide法得到了较为广泛的应用，全世界的各个浓缩机制造商大部分采用上述两种理论。利用两升沉降柱进行试验，试验数据经过上述模型的处理后得到UA(单位时间内处理单位重量的固体所需要的沉降面积)，根据总的固体处理量可得到总的沉降面积，从而计算浓缩机的直径。本文对上述两种方法进行分析，并对沉降实验的结果进行数据处理，得到不同底流浓度时所需的浓缩机直径，为浓缩机的选型设计提供科学的依据。

1 数学模型

1.1 Talmage-Fitch 法[3]

根据Coe-Clevenger设计方法，单位面积UA可有下述公式进行计算:

式中:ρs是固体密度;σI(Øi)是浆液浓度为 Øi时的初始沉降速度;Øu是底流固体浓度。Coe和Clevenger提出利用一系列的不同固体浓度的实验室沉降试验，可以确定最大的单位面积UA。如果被处理的固体被认为是理想悬浮液，且(Øi，fbk(Øi))满足Kynch沉降理论，一个适当的沉降试验可以提供计算UA所需要的所有信息[4]。为了计算Øi和沉降速度σI(Øi)，通过沉降曲线的任意点i作一条切线，对应于此点的固体浓度和沉降速度可由下式计算:

式中:Z和T分别为过i点的切线在纵坐标与横坐标上的截距;L是悬浮液的初始高度，Ø0是悬浮液的初始浓度，见图1.同理，底流排放浓度Øu应满足(2)、(3)式，即:

将式(2)和式(4)代入式(1)得到:

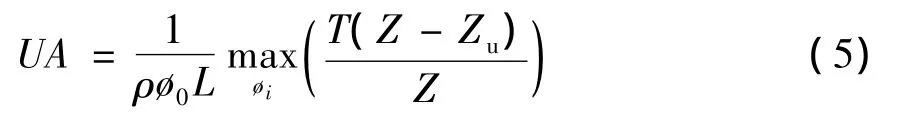
适当的沉降曲线意味着沉降试验对悬浮液初始浓度有较高的要求，初始浓度应该是固体通量曲线上影响点所对应的浓度。但是影响点处的浓度无法求得，唯一的办法是进行估计。这样有可能出现切线无法做出的情况。

Talmage和Fitch通过对沉降过程的观测发现浓度为Øi的固体的沉降速度可用下式表示:

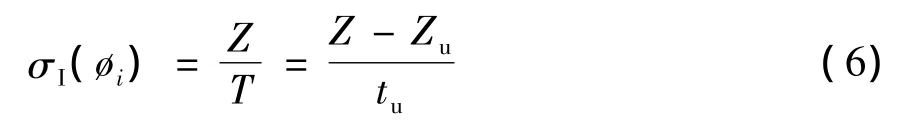
将式(6)代入到式(5)，得到:

从图1可见，当任意的界面高度Zk=Zu时，tu达到最大值tU，因此单位面积UA为:

利用式(8)可以计算出不同固体浓度，即不同沉降时间得单位面积UA.

图1 浓缩机设计模型Fig.1 Design model of thickener

1.2 Wilhelm-Naide 法[5]

在大量前人工作的基础上，Wilhelm和Naide于1978年完善了分批实验的理论，并用数学表达式给出了浓度与沉降速度、底流浓度与单位质量面积的关系。为实验数据处理提供了完整的理论依据。

连续沉降过程中，固体相对于浓缩机池壁向下的速度等于固体在重力单独作用下的沉降速度Vi与浓缩机底流排料引起的下降速度U之代数和。由重力导致的固通量等于该层浓度与该层沉降速度的乘积;由底流排料引起的固通量取决于该层浓度与底流排料速度的乘积。因此固通量(ψi)在任意浓度层的表达式为:

若沉降速度与浓度关系已知，则固通量可由方程(9)求出。图2为指定底流泵排量情况下的典型通量曲线。当底流泵排量未达最高点时，曲线上存在着一个最小值。此值限制了给定底流浓度情况下的浓缩机处理能力。若沉降速度仅为当前层浓度的函数，(假定已给出某一底流泵排量)从理论上讲，浓缩机应在这一限定值以下进行工作。否则，若底流泵排量不变，而浓缩机在高通量情况下运行，泥床高度会增加，直到从溢流堰排出。此时，固通量已经超过了浓缩机最大固通量。相反，若浓缩机固体负荷低，泥床会降低直至消失[6]。

图2 指定底流通量曲线Fig.2 Flux curve at specified underflow

极限固通量ψl由此状态下的浓度与沉降速度给出:

同时极限固通量又是底流泵排量与底流浓度的函数，根据质量不变可得:

在图2中，可以通过确定流量曲线上经过Cl点的切线来确定预期的底流浓度。底流泵排量可以由在最小限定点的浓度与沉降速度的微分方程来获得。

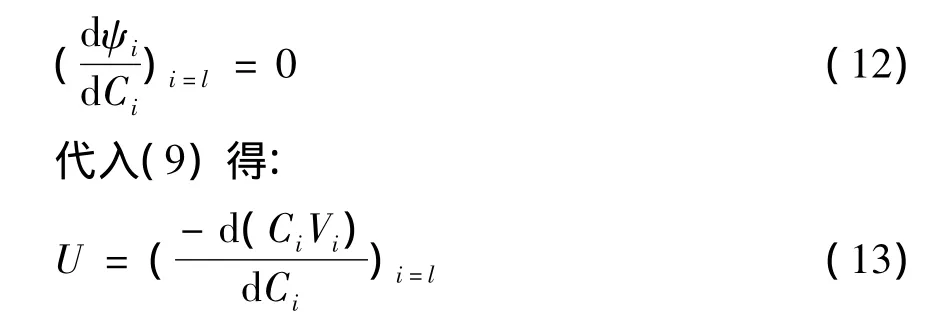
为了计算方程(13)右边的微分，必须确定出浓度和沉降速度的关系。目前还没有适用于整个浓度范围的一般化的数学表达方法，用以确定沉降速度与浓度的关系，只能通过数据拟合近似表示他们的对应关系。沉降速度与浓度的关系为:

常数a与b由分批沉降实验的数据得出。这两个常数均受颗粒大小、形状、液体与固体的密度、液体的粘度、颗粒间的吸引力及排斥力等因素的影响。

方程(14)代入方程(13)，结果为:

将方程(14)、(15)代入方程(10)，有:

再将方程(15)代入方程(11):

方程(16)除以方程(17)，可得:

方程(18)给出了极限浓度和底流浓度之间的关系。将方程(18)代入到方程(17)可得:

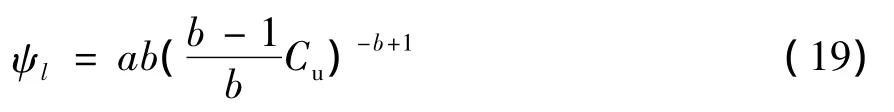
此公式建立了固通量与预期的底流浓度的关系。同样将固体通量用单位面积表示，方程(19)可变形为:

图3 浓度为4%时的沉降曲线Fig.3 Settling curve at the solid concentration of 4%

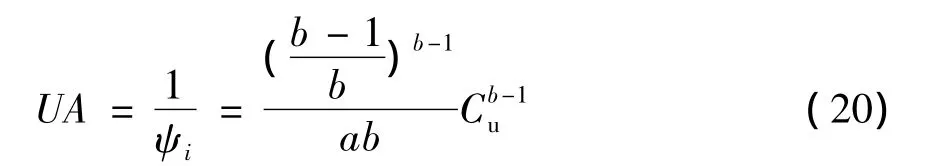
利用上式可计算出不同浓度所对应的单位面积UA.

2 试验方法

为了利用上述方法计算单位面积UA，需要进行静态浓缩试验。试验装置采用2 L沉降柱，并安装6 rpm～12 rpm的耙架机构;试验材料采用铁矿尾矿，初始固体浓度分别为4%、5%、17%和20%，固体比重为2.92;所采用的絮凝剂为聚丙烯酰胺，投加量分别为 80 g·t-1、90 g·t-1和 g·t-1.样品的沉降试验时间分别为71 min、86 min、90 min和387 min.在试验过程中，每隔一定的时间纪录泥水界面的高度，得到两组试验数据。

3 数据处理

3.1 数据结果

根据上述试验数据可绘制出不同初始固体浓度时的沉降曲线，如图3、图5、图7、图9。利用这些沉降曲线，按照上述的理论方法可得到沉降速度与固体浓度之间的关系，进而得到固体浓度与单位面积UA的关系，如图4、图6、图8、图10，从而可对浓缩机进行设计。

3.2 沉降理论的应用

在确定了固体的处理量及所需要的底流浓度，利用单位面积可达到浓缩机所需要的沉降面积，进而得到浓缩机的直径。计算实例如下:

图4 固体浓度与单位面积的关系Fig.4 The relationship of solid concentration and unit area

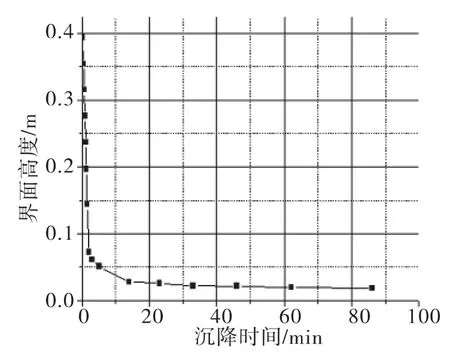
图5 浓度为5%时的沉降曲线Fig.5 Settling curve at the solid concentration of 5%

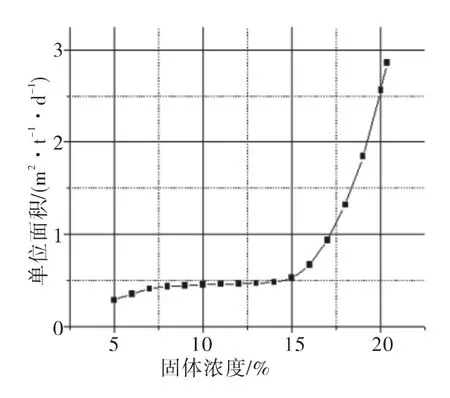
图6 固体浓度与单位面积的关系Fig.6 The relationship of solid concentration and unit area

图7 浓度为17%时的沉降曲线Fig.7 Settling curve at the solid concentration of 17%

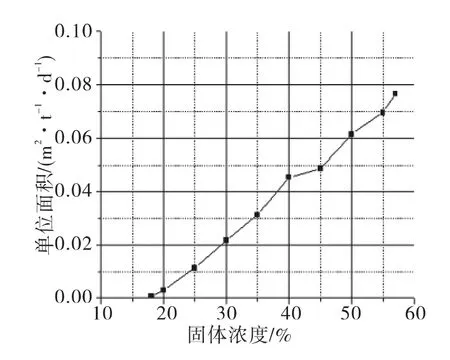
图8 固体浓度与单位面积的关系Fig.8 The relationship of solid concentration and unit area

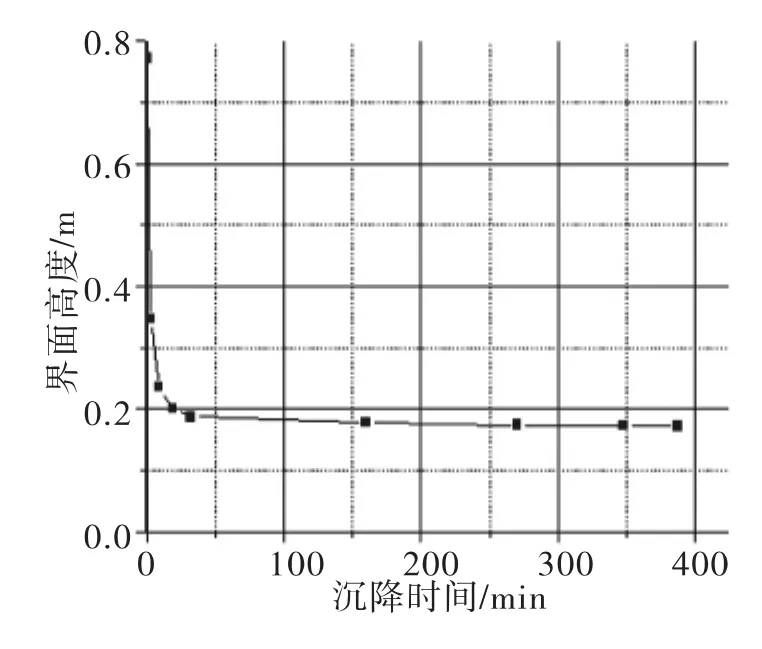
图9 浓度为20%时的沉降曲线Fig.9 Settling curve at the solid concentration of 20%

固体处理量:450(t·h-1)

给料浓度:17%

对于不同的底流浓度对应不同的单位面积UA，固体浓度从50%到56%所对应的UA分别为:0.19(m2·t-1·d-1)、0.21(m2·t-1·d-1)、0.23(m2·t-1·d-1)、0.28(m2·t-1·d-1)、0.3(m2·t-1·d-1)和 0.33(m2·t-1·d-1)，如图 8.达到这些底流浓度所需要的浓缩机直径分别为Ø51 m、Ø54 m、Ø56 m、Ø62 m、Ø64 m 及 Ø68 m.

图10 固体浓度与单位面积的关系Fig.10 The relationship of solid concentration and unit area

4 结论

与国内采用经验设计相比较，按照Talmage-Fitch设计方法和Wilhelm-Naide方法可以得到对应不同固体浓度时的单位面积UA，并可得到不同底流浓度时的浓缩机的选型，从而可合理进行浓缩机的选型设计。将沉降理论和沉降试验有机的结合起来，可提高浓缩机设计的科学性及准确性，从而保证浓缩机的工艺性能。

[1]亓欣，陈雪.浓缩机沉淀面积计算方法的探讨[J].选煤技术，2010(3):50-51.

[2]杨守志，孙德堃等.固液分离[M].北京:冶金工业出版社，2003.

[3]MARIA CRISTINA BUSTOS，FERMANDO CONCHA，RAIMUND BURGER，et al.Sedimentation and Thickening:Phenomenological Foundation and Mathematical Theory[M].Holland:Kluwer Academic，1999.

[4]吕一波，司亚梅.浓缩机技术理论及设备发展[J].选煤技术，2006(5):62-66.

[5]WILHELM J，NAIDE Y.Sizing and operating continuous thickeners[J].Mining Engineering，1981，33:1710-1718.

[6]胡钰贤，朱维耀，郭亚兵等.银川某污水厂工艺改造模拟研究[J].太原科技大学学报，2011，32(1):71-75.