中国大额支付系统节点强度分布研究
2013-10-15高鹏程
王 鹏, 高鹏程
(1. 西南财经大学 中国支付体系研究中心, 成都 611130; 2. 浙江淘宝商城技术有限公司, 杭州 311121)
0 引 言
大额实时支付系统是我国现代化支付系统的重要组成部分, 采取逐笔实时方式处理支付业务, 全额清算资金。它是连接社会经济活动及其资金运行的“大动脉”, 在金融基础设施中处于核心地位。毋庸置疑, 大额系统是典型的复杂系统。近些年来, 对于复杂系统的研究涌现出了一些新理论、 新方法, 复杂网络无疑是其中最卓有成效的理论之一[1]。由于大额系统具有复杂网络的3个典型特征: 总体结构复杂、 节点行为复杂和各种复杂因素相互影响[2]。因此, 用复杂网络理论研究支付系统, 不仅是可行的, 而且有可能获得很多传统方法无法得到的结果, 这已经成为学术界和业界的共识[3,4], 并且产生了一大批成果[5-9]。
在现有的成果中, 有很大一部分工作集中于支付网络的拓扑性质的研究。这是因为了解支付网络的拓扑结构是进一步工作的基础。而在支付网络的拓扑性质中, 节点强度分布又是最重要的。笔者主要研究我国2006~2009年间大额支付系统地区间资金流网络的节点强度分布问题。以地区为顶点, 以地区之间的交易金额和交易笔数为边权重, 建立交易金额复杂网络模型和交易笔数复杂网络模型。这是将大额支付系统的交易数据按照其地区的属性重新组织, 从地区角度研究支付系统交易资金流, 更加强调支付系统网络的经济意义。大额支付系统地区间资金流网络所反映的不是支付系统本身的风险、 拥塞等问题, 也不是对直接参与者的流动性研究, 而是反映区域经济发展、 地区间经济往来、 资金流量等方面的问题, 从宏观的角度为区域经济发展策略、 国家经济发展战略提供更有价值的参考信息。
1 节点强度分布及其估计方法
从边是否被赋权的角度看, 复杂网络可被分为无权网络和有权网络两类。对于无权网络而言, 度分布、 平均路径长度和聚集系数等都是描述其拓扑结构的重要参数。其中度分布在多数情况下是最重要的。因为在节点重要性的刻画、 确定是否为同构图等问题上, 都要以度分布函数为依据[1,2]。而对于有权网络而言, 由于各条边都是带权的, 因此度分布的概念就变为节点强度分布。可以说节点强度分布是度分布概念的推广。
1.1 节点强度分布的概念
节点强度是加权网络区别于无权网络的重要几何量, 它类似于无权网络中度的概念, 也是一个测量节点重要程度的拓扑参数。一个节点的强度si是指与其所连接的所有边的权重之和, 即
(1)
其中Γi为i的邻居节点集合。在不同的复杂网络中, 节点强度有着不同的含义。如, 在航空网络中, 节点强度表示一个站点的运输能力; 而科研合作网络中, 节点强度表示一个科研学者科研能力的强弱。与度分布的概念类似, 在有权网络中节点强度也有自己的分布。
1.2 节点强度分布的估计方法
大量的研究表明, 多数复杂网络, 包括支付系统网络的节点分布服从幂律分布[1,10-14]。幂律(Power Law)分布是一种特殊的数量关系, 当一个事件的发生频率与该事件的某个属性之间是一种幂函数的关系时, 称该事件的发生频率服从幂律分布。可理解为在一个系统中, 规模较小的事件会经常发生, 但规模很大的事件却极少发生。幂律分布有一个独特的现象, 被称为“长尾现象”, 就像一个国家的国民收入, 少部分人掌握着国家的大部分财富, 而大部分人只拥有很少财富, 即经常说的“二八定律”, 实际上二八定律也是对长尾理论的粗略描述。幂律分布的一般表达式可以表示为:p(x)=Cx-α。
当发现样本数据具有幂律分布性质时, 为精确掌握数据的分布, 需要对幂律分布的参数进行估计。通常情况下使用最小二乘法对幂指数进行估计, 但最小二乘对幂指数的估计有可能产生不准确的结果[15], 因此笔者选择了极大似然估计方法。
在幂律分布的分布函数有两个参数需要估计: 幂指数α和分布下界xmin。虽然在自然界和现实生活中有大量服从幂律分布的现象存在, 但是, 大部分样本都不完全服从幂律分布, 一般的情况是大于某一个最小值xmin的数据服从幂律分布, 这时称xmin为幂律分布的下界, 在估计α时假设xmin已知, 并来自样本。极大似然估计法的基本思想是: 在一次观测中某一事件出现了, 则认为此事件出现的可能性很大。在概率论中, 密度函数p(x,α)扮演了重要角色。当α已知时,p(x,α)显示概率密度函数随x变化的情况。而当有了样本数据x后, 则可考虑对不同的α, 概率密度的变化情况, 它反映了对x的解释能力, 这便是似然。极大似然估计就是要寻找使这种可能性或似然达到最大的未知参数α。
进行极大似然估计要得到样本的联合密度函数, 即似然函数为
(2)
对式(2)两边同时求对数得
(3)
为求P(x)的最大值, 即求L(α)的最大值, 令
(4)

(5)
其中xi∈{xi≥xmin(i=1,2,3,…,n)}, 标准差为
(6)
在进行极大似然估计时, 首先假定样本服从幂律分布, 然后求出似然函数和使似然函数值最大的参数做为幂指数的估计。极大似然估计并不会对数据是否服从幂律分布进行检验, 其估计值是拟合极大似然估计最好的值。所以, 在参数估计之后需要对样本是否服从幂律分布进行假设检验。
对样本是否服从幂律分布进行检验的一个可行的办法是检验样本和幂律分布数据的距离, 如果距离很大, 则样本不服从幂律分布; 反之, 则服从幂律分布。由于KS检验对非正态数据的检验非常有效, 所以在检验幂指数时选择了KS检验。KS检验计算距离的公式为
(7)
其中S(x)为样本中大于xmin的数据的累积分布函数,P(x)为x>xmin的幂律分布的累积分布函数。
生成服从某种分布的随机数据有很多种方法, 笔者采用简单而有效的转换法[16]。设p(x)为x>xmin的概率密度函数,r为(0,1)上服从均匀分布的随机变量, 概率密度函数p(x)和p(r)关系如下
(8)
根据x的累积分布函数可得

(9)
求得
x=xmin(1-r)-1/(α-1)
(10)
根据幂律分布的生成规则进行KS检验。首先, 估计原始数据的幂指数α, 然后根据生成规则生成大量服从幂指数为α、 下界为xmin的幂律分布数据, 最后用原始数据和生成的数据做KS检验。为得到比较准确的结果, 在生成的测试数据中, 大于xmin部分的应该服从幂律分布, 小于xmin的部分的分布应该和原始数据相同。假设原始数据样本量为n,x>xmin的样本量为ntail, 服从幂指数为α、 下界为xmin的幂律分布数据为xpl, 原始数据中x 笔者的研究对象是2006~2009年大额支付系统地区间资金流, 时间单位为年, 包括北京、 天津、 河北、 山西、 内蒙古、 辽宁、 吉林、 黑龙江、 上海、 江苏、 浙江、 安徽、 福建、 江西、 山东、 河南、 湖北、 湖南、 广东、 深圳、 海南、 广西、 重庆、 四川、 贵州、 云南、 西藏、 陕西、 甘肃、 青海、 宁夏、 新疆共32个地区, 其中深圳为单独样本, 不从属于广东。数据来源于《中国支付体系发展报告》(2006~2009)公布的大额支付系统地区间资金流量流向情况年报表, 包括交易金额和交易笔数两个方面。 如果使用原始数据, 则资金流网络应该是一个有向加权带环的完全网络。为把要研究的问题简单化并尽量保持原有数据的信息, 将每两个地区间的资金往来加总, 把有向的资金流网络转换成无向资金流网络, 消除资金往来的方向性, 这样在保持了数据的原有信息下更方便观察网络的拓扑结构。同时, 笔者要研究的是地区间的资金流网络, 所以不考虑地区内部的资金流转, 体现在网络结构上是一个去环的过程。至此, 研究对象就成为一个具有32个节点、 496条边的无向无环加权的完全网络。 观察网络结构的最直观的方法是以图形的方式画出其结构。这里选取了2006年的交易金额和交易笔数的网络图做为例子进行展现, 如图1所示。 a 交易金额网络结构 b 交易笔数网络结构 笔者所研究的大额支付系统网络是一个节点数固定、 完全连通的网络, 节点的度均相同, 对节点度分布的研究的现实意义不大, 因此研究的重点是节点强度的分布。大量对其他国家支付系统的实证研究显示, 支付网络的节点强度分布普遍具有幂律分布的性质[10-12]。 通过使用极大似然估计方法, 同时进行KS检验, 进行了多次估计取均值的节点强度拟合, 效果如图2所示。 a 2006年 b 2007年 c 2008年 d 2009年 从拟合图上发现交易金额网络节点强度并不完全服从幂律分布, 在每个分布图的前部都会有垂头的现象存在, 这部分数据不符合幂律分布, 而之后的大部分数据具有较好的拟合效果, 都分布在拟合直线的周围。具体的估计结果如表1所示。 表1 交易金额网络节点强度分布拟合结果 其中mlea为幂指数α的估计结果, std为估计标准误差, l_xmin为幂律分布下界位置比例。首先从分布下界的位置比例来看, 除了头部的几个数据, 样本基本服从幂律分布, 其均值为1.418, 交易金额网络边权分布的幂指数均值为1.4, 二者几乎相等。某节点的强度是与其相连的边的权重之和, 这就决定了节点强度的分布和边的权重有很大关系, 它与通常度所代表的含义有很大区别。 交易笔数网络节点强度分布拟合图如图3所示。 a 2006年 b 2007年 c 2008年 d 2009年 交易笔数网络的节点强度分布和交易金额网络一样, 不完全服从幂律分布。其节点强度分布的前部和交易金额略有不同, 每年节点强度分布的前部都有一个小的波动, 交易金额节点强度分布前部虽然有垂头现象, 但整体上没有波动。交易笔数网络的节点强度除了小部分的前部数据不符合幂律分布外, 大部分数据都服从幂律分布, 并且其节点强度分布中处于幂律分布下界之上的数据在双对数坐标下更接近于直线。交易笔数网络节点强度的幂律分布参数估计结果如表2所示。 表2 交易笔数网络节点强度分布拟合结果 幂律分布下界位置比例显示, 只有少数样本不服从幂律分布, 大部分的样本服从幂律分布, 其均值为1.5, 与交易笔数网络边权分布的幂指数估计值有所区别, 但差距不大。 图4 节点强度分布幂指数趋势图 虽然交易金额网络节点强度和交易笔数节点强度在各自的幂律分布下界之上都服从幂律分布, 但其幂律分布的幂指数有区别。从图4中可看出, 2006~2009年交易笔数节点强度分布的幂指数始终大于交易金额网络。尽管两个网络节点强度分布的幂指数的大小不同, 但其变化趋势十分一致。 验大额支付系统的地区间资金流网络是一个加权的完全网络, 虽然节点之间完全连通, 节点度都相同, 但节点强度却因为边权的不同而有很大差异。无论是交易金额网络还是交易笔数网络, 其边权的分布具有右偏态特征和长尾特性。鉴于边权的这种特征, 必将关注权重对网络结构的影响。为了研究这种影响笔者也采用了设置阈值的方法。在研究权重较小的边对网络结构的影响时, 设置阈值从最小值开始变化到最大值, 当网络中两个节点之间的权重小于设定的阈值时, 则认为这两个节点没有连接; 在研究权重很大的边对网络结构的影响时, 设置阈值从最大值开始变化到最小值, 当网络中两个节点之间的权重大于设定的阈值时, 则认为这两个节点没有连接。阈值每变化一次都会通过极大似然估计和KS检验求得节点强度分布的幂指数。 为减小计算量, 设置阈值时采取了不等步长的变化方法, 即在边权较小时, 阈值变化的步长也小, 当边权较大时, 阈值变化的步长也大。阈值从小到大变化时节点强度分布幂指数变化如图5所示。 a 交易金额网络幂指数变化趋势 b 交易笔数网络幂指数变化趋势 图5中4条曲线分别代表4年的变化趋势。交易金额网络每年的变化趋势基本相同, 交易笔数网络也相同。两个网络节点强度分布的幂指数都会随着阈值的变大而变大, 但交易金额网络的变化十分迅速, 其速度要远大于交易笔数网络。交易金额网络的幂指数从1.4左右开始直线上升到1.8左右, 之后有一个相对平稳的阶段。随着阈值变化到一个临界值后, 其幂指数从1.8再次直线上升到3.0左右, 网络结构发生了较大的变化。而交易笔数网络的幂指数则从1.5左右开始随着阈值的增长缓慢增长, 在增长过程中并没有出现相对平稳的阶段, 而且其幂指数始终大于交易金额网络。 当阈值从大到小变化时, 幂指数的变化也不相同, 如图6所示。交易笔数网络和交易金额网络的幂指数随着阈值由大到小变化都经历了3个阶段, 1) 平稳变化期; 2) 快速上涨期; 3) 震荡下降期。当阈值较大时, 交易金额网络和交易笔数网络的幂指数的变化都十分平稳, 去掉权重较大的边不会对网络的结构产生太大的影响。阈值变化超过某个临界值后, 两个网络的幂指数都进入了快速上涨期。交易笔数网络每年的幂指数增长速度基本相同, 临界值也基本相同, 但交易金额网络则不相同, 2006年和2009年的网络的幂指数上升速度很大, 2007年和2008年基本上没有太大的上升就进入了震荡下降期。 a 交易金额网络幂指数变化趋势 b 交易笔数网络幂指数变化趋势 从整体上看, 阈值从小到大变化和从大到小变化对两个网络的幂指数影响的区间是相同的, 交易金额网络的幂指数变化区间在1.4~3.0之间, 交易笔数网络的幂指数变化在1.5~4.0之间。但是, 权重小的边对网络结构的影响大于权重大的边。无论阈值从小到大变化还是从大到小变化, 当阈值较小时, 幂指数都会有相对强烈的震荡, 而当阈值较大时, 幂指数则趋于稳定。同时, 交易金额网络各年幂指数变化的临界值也不相同。 复杂网络的小世界性质是近年来一个研究热点[1], 探讨网络的小世界性质也成为必做的工作。通常, 人们用两个指标说明网络的小世界性质: 聚集系数(Clustering Coefficients)和平均路径长度(Average Path Length)。根据Barrat算法, 节点i的聚集系数 (11) 其中ki为节点度,Ei为与节点i相邻的节点之间实际存在的边数。整个网络聚集系数就是所有结点聚集系数的平均值。 平均路径长度 (12) 其中N是网络的结点总数,dij是连接两个节点的最短路径的边数。 一个具有小世界特性的复杂网络, 应该是同时具有较高聚集系数和较低的平均路径长度[1]。为进一步说明支付系统网络的拓扑特征, 按交易金额(单位: 亿元)和笔数(单位: 万笔)两个指标, 计算了对应的聚集系数和平均路径长度, 以此来说明支付系统网络的小世界特性。限于篇幅, 只给出2009年支付系统网络的计算结果(见图7)。图7中, 在相同的阈值下, 无论是对交易金额还是交易笔数, 支付系统网络同时具有较低的聚集系数和较高的平均路径长度。这些计算结果说明大额支付系统网络不具有小世界特性。 a 交易金额网络 b 交易笔数网络 以地区为节点, 以交易金额和交易笔数为边建立的大额支付系统复杂网络的节点强度分布基本都服从幂律分布。另外, 两个幂指数有所不同, 交易金额网络的幂指数总是大于交易笔数网络的幂指数。通过改变边权的阈值也会改变网络到幂指数。幂指数的变化还有一个临界现象存在, 当阈值大于某个临界值时, 幂指数就会趋于稳定, 而小于该临界值时, 幂指数就会强烈的波动, 该临界值还会使网络结构产生较大的变化。最后, 探讨了支付系统网络的小世界性质, 指出大额支付系统网络没有小世界特性。 参考文献: [1]ALBERT R, BARABASI A. Statistical Mechanics of Complex Networks [J]. Reviews of Modern Physics, 2002, 74(1): 47-97. [2]汪小帆. 复杂网络理论及其应用 [M]. 北京: 清华大学出版社, 2006. WANG Xiao-fan. The Theory and Application of Complex Networks [M]. Beijing: Tsinghua University Press, 2006. [3]崔海蓉, 何建敏. 基于复杂性网络理论的银行系统性风险研究评述 [J]. 西安电子科技大学学报: 社会科学版, 2009, 19(4): 12-18. CUI Hai-rong, HE Jian-min. Systemic Risk in Banking Based on Complex Network Theory [J]. Journal of Xidian University: Social Science Edition, 2009, 19(4): 12-18. [4]UROPEAN CENTRAL BANK. Financial Networks and Financial Stability [R]. Financial Stability Review Frankfort: European Central Bank Press, 2010: 155-160. [5]童牧. 中国大额支付系统稳健性的仿真模拟 [J]. 吉林大学学报: 信息科学版, 2012, 30(2): 171-179. TONG MU. Simulation Study on Robustness of China’s Large Value Payment System [J]. Journal of Jilin University: Information Science Edition, 2012, 30(2): 171-179. [6]童牧. 大额支付系统中的系统风险及其决定因素研究 [J]. 吉林大学学报: 信息科学版, 2012, 30(3): 297-305. TONG MU. Systemic Risk and Its Determinant in Large Value Payment System [J]. Journal of Jilin University: Information Science Edition, 2012, 30(3): 297-305. [7]贾彦东. 金融机构的系统重要性分析 [J]. 金融研究, 2011, 376(10): 17-33. JIA Yan-dong. The Analysis of Systemic Importance of Financial Institution [J]. Journal of Financial Research, 2011, 376(10): 17-33. [8]尤学智. 电子商务网络支付的发展研究 [J]. 吉林大学学报: 信息科学版, 2010, 28(6): 616-624. YOU Xue-zhi. Research on Development of Network Payment in E-Commerce [J]. Journal of Jilin University: Information Science Edition, 2010, 28(6): 616-624. [9]王莹. 电子支付市场的创新策略与演化 [J]. 吉林大学学报: 信息科学版, 2012, 30(4): 409-417. WANG Ying. Innovation Strategy and Evolution on E-Payment Market [J]. Journal of Jilin University: Information Science Edition, 2012, 30(4): 409-417. [10]BOSS M. Network Topology of the Interbank Market [J]. Quantitative Finance, 2004, 4(6): 677-684. [11]INAOKA H. Fractal Network Derived from Banking Transaction: an Analysis of Network Structures Formed by Financial Institutions [EB/OL]. (2001-05-06). [2013-07-16]. http://www.boj.or.jp/en/research/wps_rev/wps_2004/wp04e04.htm/. [13]WETHERILT A. The Sterling Unsecured Loan Market During 2006~2008:Insights from Network Topology [EB/OL]. (2010-06-06). [2013-07-06]. http://www.bankofengland.co.uk/research/Pages/workingpapers/2010/wp398.aspx. [14]BECH M, ATALAY E. The Topology of the Federal Funds Market [J]. Physica A, 2010, 389: 5223-5246. [15]CLAUSET A. Power-Law Distributions in Empirical Data [J]. SIAM Review, 2009, 51: 661-704. [16]TEUKOLSKY SA. Numerical Recipes in C: the Art of Scientific Computing [M]. Cambridge: Cambridge University Press, 1992.2 数据描述和网络生成

3 大额支付系统网络节点强度分布研究
3.1 大额支付系统网络节点强度分布


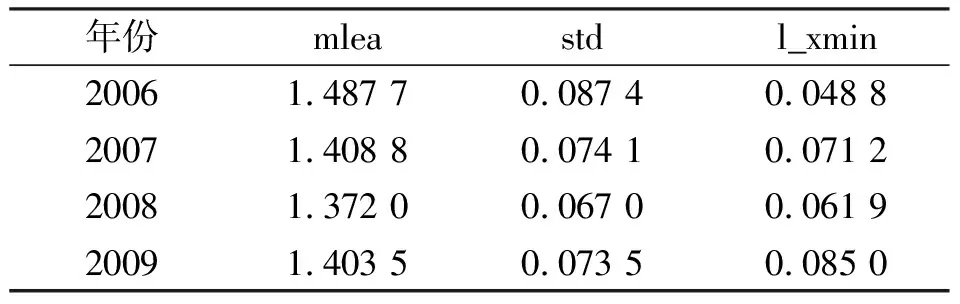
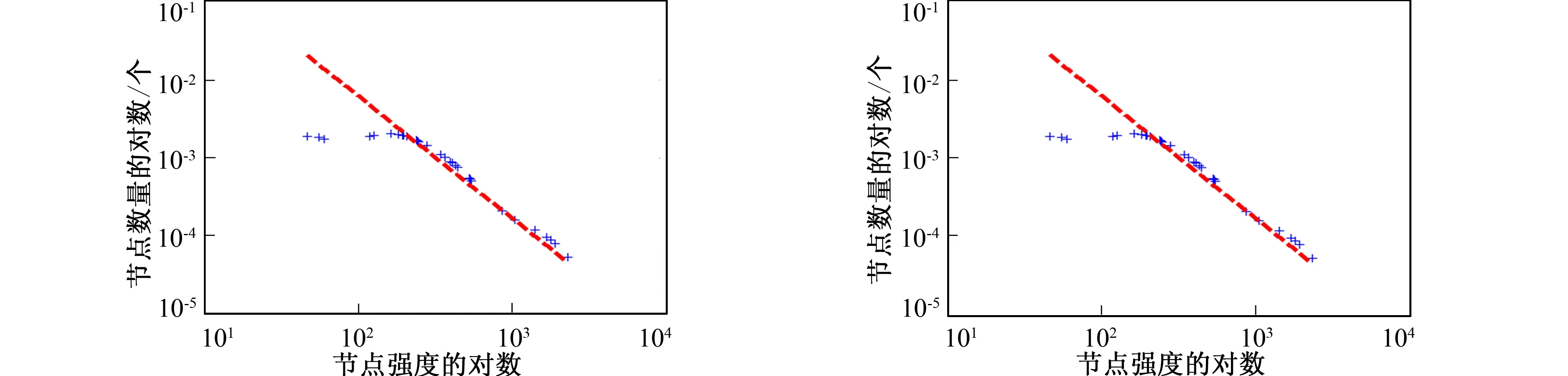


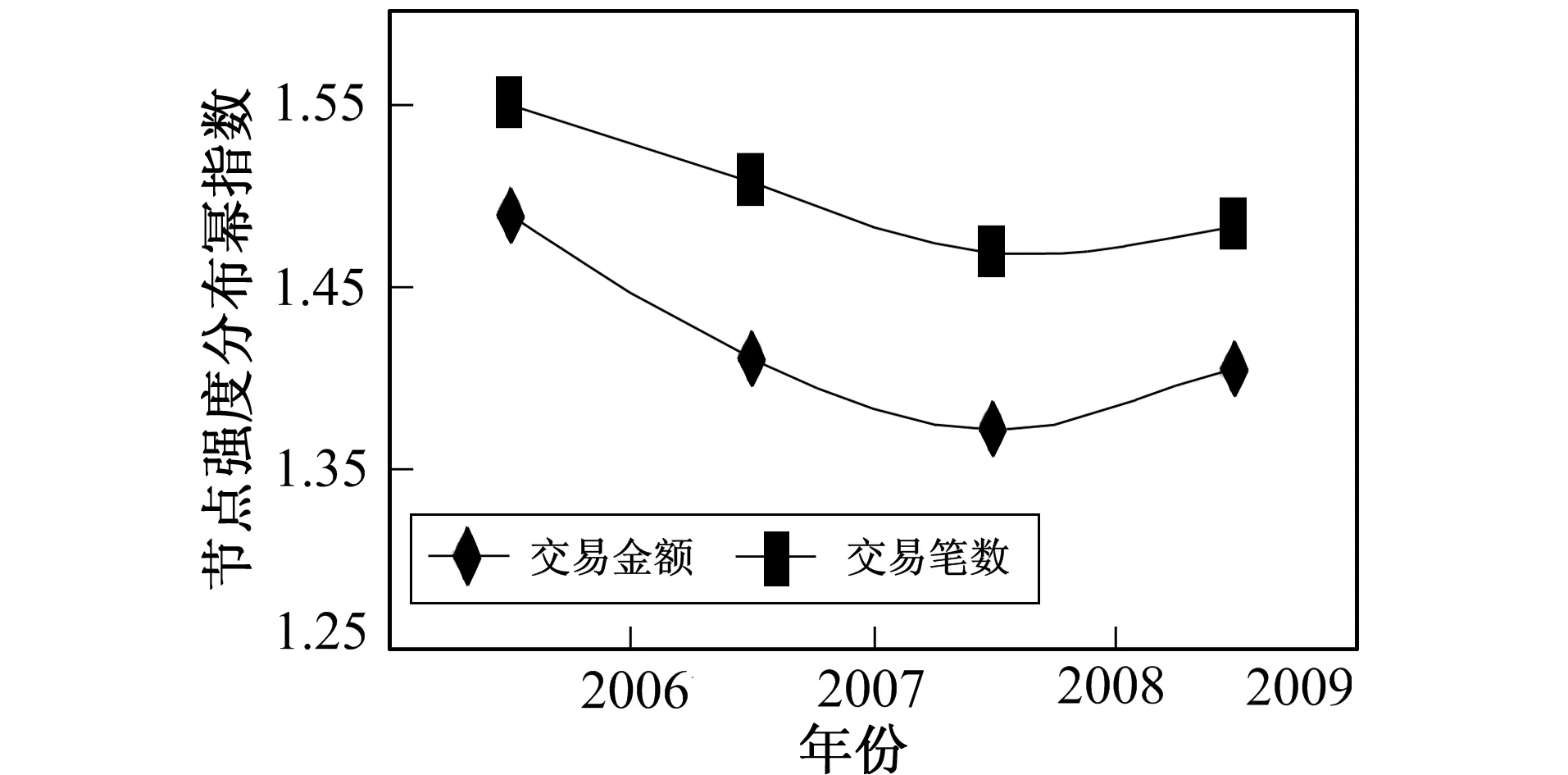

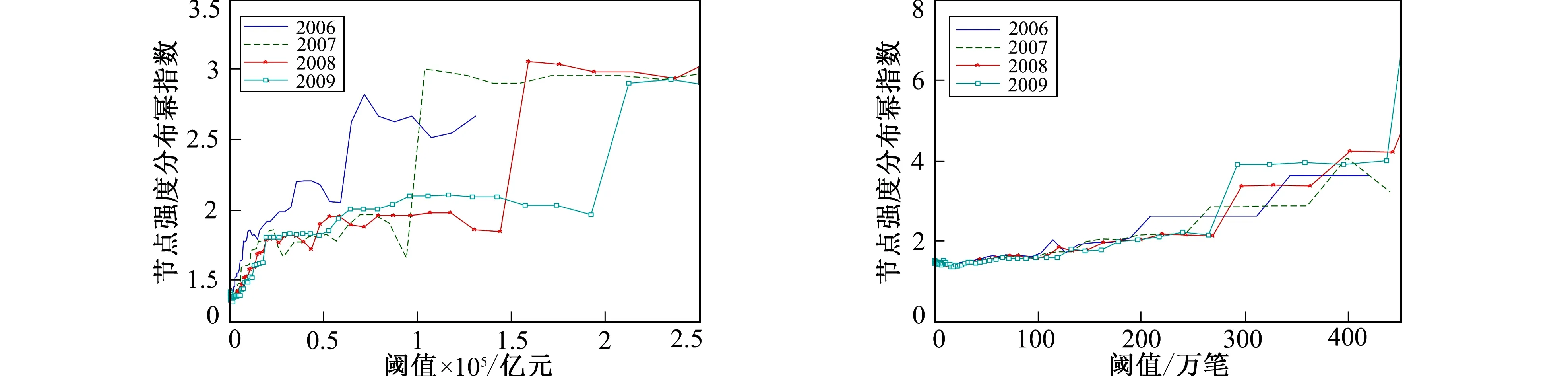
3.2 阈值变化对节点强度分布参数的影响

4 支付系统网络的小世界性质

5 结 语
