基于双重阈值近邻查找的协同过滤算法
2013-10-15李永丽蔡观洋
李 颖, 李永丽, 蔡观洋
(1. 吉林师范大学 计算机学院, 吉林 四平 136000; 2. 东北师范大学 计算机科学与信息技术学院, 长春 130117;3. 吉林大学 计算机科学与技术学院, 长春 130012)
0 引 言
个性化推荐在当前互联网服务行业的地位越来越重要, 它是解决信息过载的重要方式。协同过滤算法则是个性化推荐算法中应用最成功的一种技术, 该算法实现简单, 部署方便, 在商业领域得到广泛应用[1], 很多学者对其进行了深入全面地研究, 以克服该算法在应用过程中的不足。
协同过滤算法, 也叫社会过滤算法, 它充分利用“人”这个元素的社会属性。社会中的每个人都有一些和自己兴趣相似的个体, 本算法基于这样的假设: 一个人可能更喜欢和他兴趣相投的人所感兴趣的项目。该算法是在系统的所有用户行为数据上进行学习的, 不需要考虑项目的内容信息。因此, 对非结构化的信息, 如电影、 音乐和视频等, 可以产生不错的推荐结果。但是, 该算法仍存在许多不足, 如由数据稀疏性导致的推荐精度不高, 用户/项目冷启动和推荐多样性等问题[2]。其中推荐精度作为衡量个性化推荐算法的重要指标, 得到了学者的重视, 并提出了许多方式用以提高推荐精度。
George等[3]为了降低活跃用户对推荐结果影响, 通过归一化用户评分项目组的出现频率, 对用户的每个评分项目都添加一个归一化因子, 然后参与到用户/项目间的相似性计算中。因此, 降低了那些被活跃用户评价过的项目在推荐过程中的重要度。Yue等[4]提出了“细粒度”的相似性分析法, 期望挖掘那些兴趣与目标用户部分一致的用户, 提高推荐精度。除了上述针对如何充分利用用户项目评分矩阵信息外, 还有其他一些方式用以提高推荐精度, 如Sarwar等[5]提出的奇异值分解技术能降低稀疏评分矩阵的维数, 提高项目或用户间的相似性准确度, 从而提高推荐精度。
这些方法虽然都从协同过滤算法的基础----项目/用户间的相似性计算准确度提出了有效方法, 但都没有考虑最终近邻用户组或近邻项目组从候选集的筛选过程, 由于最终的推荐结果是以近邻用户组/项目组为计算依据的, 因此它们的质量直接关系着推荐精度。笔者从近邻用户/项目组的筛选入手, 分析了近邻用户组与推荐精度间的关系, 提出了基于双重阈值的近邻查找方法, 并将此方法应用在基于用户的协同过滤算法(UBCF: User Based Collaborative Filtering)和基于项目的协同过滤算法(IBCF: Item Based Collaborative Filtering), 通过离线实验证明了该方法可有效提高推荐精度。
1 相关知识
1.1 协同过滤算法步骤
协同过滤算法是目前研究最热的一种个性化推荐技术, 一般分为3个步骤: 用户信息数据表示; 邻居用户组/项目组的查找; 生成推荐列表。下面以基于用户的协同过滤为例说明每个步骤实现细节。
1) 用户信息数据收集与表示。用U={u1,u2,…,um}表示用户集合,I={i1,i2,…,in}表示系统中的项目集合, 其中系统中共有m个用户,n个项目, 用矩阵Rm×n表示系统中所有的用户对项目的评分信息[6], 矩阵中的元素Rui表示用户u对项目i的评分信息。
2) 邻居用户/项目的查找。查找邻居用户组/项目组是协同过滤算法中最重要的一步, 其主要是用户集合中找出与目标用户u兴趣最相似的k个用户N={u1,u2,…,uk}, 使Ssim(u,u1,…,k)>Ssim(u,uk+1,…,m),Ssim(u,v)表示用户u和用户v的相似度。常用的相似性计算有3种: 余弦相似性, Pearson相关相似性和修正的余弦相似性[7,8]。
3) 生成推荐列表。根据第2步生成的邻居集合, 可以依据邻居的评分信息预测目标项目的评分信息, 推荐结果有两种展示形式: 产生用户的TopN推荐; 生成目标用户的每个未评分项目的预测评分, 按从高到低的顺序排列。
1.2 近邻用户评价指标
笔者提出了近邻组相似度和参考近邻比例两个指标评估算法选出的近邻组的质量。
近邻组相似度
(1)
其中N(u,m)表示用户u在计算项目m的评分信息时近邻用户组, |N(u,m)|表示此近邻用户组的元素个数, 若计算系统的近邻用户组相似度, 则将测试集中所有记录的SNsim(u,m)相加再求平均值即可。
参考近邻比例
(2)
其中K表示计算过程中输入的近邻个数。系统的整体参考近邻比例为测试集中所有RNiebr(u,m)的平均值。
1.3 传统算法存在的不足
传统协同过滤算法在选择近邻用户组时, 或者选择全局最优的K个用户, 或者选择那些既评价过目标项目又与目标用户相似的K个用户, 但由于数据的稀疏性导致这些用户不能参与到预测评分的计算。因此, 如何充分利用现有用户评分矩阵所提供的信息, 选择合适的近邻用户组是协同过滤算法的关键。
2 算 法
2.1 双重阈值近邻查找策略
由1.3节的分析可知选择合适的策略找出一些相似性较高的项目或用户作为目标用户的近邻用户组对系统性能的影响也非常重要, 如果选择的近邻用户组并非与目标用户相近, 则会直接影响推荐质量。基于Zhang等[9]提出的近邻用户选择策略的启示, 笔者提出了双重阈值近邻查找法(DT: Dual Threhold)。
采用双重阈值近邻查找法查找目标用户或项目的K个近邻的具体步骤如下:
1) 首先将目标用户/项目与用户集或项目集中所有其他用户或项目的相似性从高到低排序。选择前N个项目或用户作为候选集C1;
2) 计算候选集C1中用户和项目的平均相似度作为相似度阈值, 再以此阈值为基础, 选择相似性大于等于此阈值的用户或项目添加到候选集C2中;
3) 从候选集C2中选择对目标项目有评分信息的用户, 或目标用户对项目有评分信息的项目, 且最相似的K个元素添加到近邻组C3中;
4) 如果近邻组C3的长度小于K, 则从C2中优先选择相似度最高且未出现在C3中的元素添加到C3中。
2.2 双重阈值近邻查找策略分析
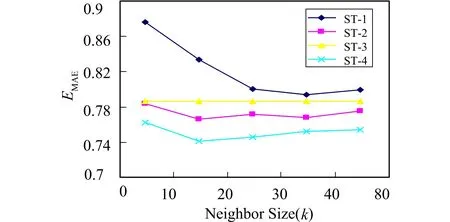
以基于用户的协同过滤算法为例分析此近邻查找方法的优势。设针对每个目标用户, 需要查找k个近邻用户, 对目标项目评价过的用户个数为r, 用户集合的大小为M, 项目集合的大小为N。因为查找近邻的过程就是扫描所有用户集合的过程, 所以通过考察查找近邻时需要查看用户的个数为基础比较算法的时间复杂度。以计算目标用户U1对目标项目I1的运算为例, 双重阈值近邻算法中假设在查找相似度阈值时考察β×k个相似性最高的用户, 只需目标用户U1对应的链表行L1即可。此链表表示目标用户与用户集合中其他用户间的相似性组成的节点链, 且链表已按相似性降序排序, 因此只需考察2βk个用户即可。当选择对目标项目已评分且与目标用户U1最相似的k个用户作为近邻时(SR1: Similarity and Rating), 若仍旧按优化方式存储用户间相似性, 由于对目标项目已评分的用户随机分布在链表L1中, 可假设r个用户将链表中的用户分成(r+1)份, 而每个用户都是等概率分布在各个份中的, 所以每份中大概有(M-r)/(r+1)个用户。当找到最相似的前k个且对目标项目有评分的用户需要访问大约k(M-r)/(r+1)个链表中的元素。此时若笔者提出的近邻查找方法DT的性能要优于上述策略SR1, 则需要满足2βk 为了测试此近邻选择策略的有效性, 将该方法应用于基于用户的协同过滤算法中, 形成新的算法----基于双重阈值的用户协同过滤算法(DT-UBCF: Dual Threshold User-Based Collaborative Filtering), 以提高算法的推荐精度。 与1.1节中的协同过滤算法步骤类似, 只是笔者的算法利用了双重阈值近邻查找方法, 因此, 每个步骤的实现细节略有差异。 1) 近邻用户组选择。采用2.2节中的双重阈值近邻查找策略; 用户间的相似性计算采用性能较好的Pearson相关相似性计算[7]。Herlocker等[10,11]通过增加一个相关重要性权重因子降低共同评分信息少的用户/项目间的相似性, 因此, 采用优化后的相似性计算公式度量用户间的关系。 用户向量u和v之间的Pearson相关相似性为Ssim(u,v)′、 最终相似性为Ssim(u,v) Ssim(u,v)=αSsim(u,v)′ (3) 其中|u|表示两个用户间的共同评分项目个数,γ代表公共评分项目阈值, 是一个正整数或0。 2) 计算目标用户对目标项目的预测评分。由于近邻用户组可能由与目标用户相似性高且对目标项目有评分行为的用户以及相似性最高但并没有评价过目标项目的用户两部分用户组成。因此, 计算预测评分时可通过设置一个参数μ调整这两部分近邻用户对计算的贡献度。由于第2部分近邻用户并没有对目标项目进行评分, 因此采用该用户的平均分取整, 并随机加0或加1作为该用户对目标项目的评分参与计算, 其公式如下 (4) 双重阈值的基于用户的协同过滤算法伪代码: 算法名称: DT-UBCF算法 输入: 目标用户userid, 目标项目itemid, 近邻用户个数neibnum, 共同评分项目阈值commRate, 计算相似性阈值的参考近邻比例belta, 两种近邻用户的贡献比例ratio, 训练集用户—项目评分矩阵trainMatrix 输出: 目标用户对目标项目的预测得分predictRate 算法描述: DTUBCF(userid, itemid, neibnum, commRate, belta, ratio, trainMatrix)//双重阈值UBCF //计算userid与其他用户间的相似性 simUser ← GETSIMILARITY(userid, commRate, trainMatrix) neighbors ← GETNEIGHBOR (simUser, belta, neibnum, itemid, trainM) //计算目标用户对目标项目的预测得分 rate ← GETPRERATE (userid, itemid, neighbors,ratio,trainM) return rate GETNEIGHBOR (simList, belta, neibnum, itemid, tMatrix)//查找目标用户的邻居 tmpList ←simList[0…belta*neibnum] SsimThre ← AVERAGE(SsimT[tmpList])//相似性阈值 foreach cell in tmpList do if len[neighbors_1]=neibnum then exit if simT[cell]≥simThre and tMatrix[user[cell]][itemid]≠0 then INSERT(neighbors_1, cell) if len[neighbors_1] foreach cell in tmpList do if len[neighbors_2]=neibnum-len[neighbor_1] then exit if cell not in neighbors and tMatrix[user[cell]][itemid]≠0 then INSERT(neighbors_2, cell) return (neighbors_1, neighbors_2) 由于基于项目的协同过滤算法与基于用户的协同过滤算法类似, 只是考察的方向不同, IBCF同样需要寻找目标项目的近邻项目组, 也可通过将双重阈值近邻查找策略应用在IBCF中形成双重阈值的基于项目的协同过滤算法(DT-IBCF: Dual Threshold Item-Based Collaborative Filtering), IBCF与UBCF算法步骤大体一致, 此处不做详细介绍。 笔者的研究重点是近邻的选择对算法推荐精度的影响, 因此, 实验过程中, 主要测试采用不同的近邻选择方法时对基于用户的协同过滤和基于项目的协同过滤算法精度的影响。协同过滤算法也要求用户输入一些参数信息, 因此实验还需测试不同参数对算法性能的影响。 实验采用5折交叉验证方法, 将MovieLens数据集均匀随机分成5份, 轮流将其中的4份作为训练集, 1份作为测试集, 所以训练集和测试集大约分别占所有评分信息的80%和20%。取5次实验结果的平均值作为此算法的最终性能结果[12]。算法性能的评估可通过对预测分值与项目的真实分值做比较得到。 笔者提出的算法是进行评分预测推荐的, 针对预测评分推荐的评估, 主要通过度量系统产生的预测分值与用户对项目的真实评价分值之间的差额大小评判推荐系统的表现, 差额越小, 说明推荐结果越准确; 反之, 则推荐性能越差。为了评估协同过滤算法的推荐精度, 学者提出了很多方法, 如MAE(Mean Absolute Error), MSE(Mean Squared Error), RMSE(Root Mean Squared Error)等, 而更多的研究者使用MAE作为度量标准[13], 实验中也采用该方法评价算法的性能, 其计算如下 (4) 其中Rui是用户u对项目i的评分,rui是推荐系统的预测评分信息,T代表测试集合。 近邻的选择策略直接影响算法的推荐精度, 通过实验比较以下4种近邻选择策略对算法的影响。 1) ST-1: 选择全局相似性最靠前的k个用户作为近邻用户; 2) ST-2: 选择对目标项目有评分信息, 且相似性最高的k个用户作为邻居; 3) ST-3: 设定一个相似度阈值SsimT, 大于此阈值且对目标项目有评分信息的都作为近邻参与计算; 4) ST-4: 取相似性最靠前的βk个用户, 以他们的相似性均值作为相似性阈值, 然后取相似性大于相似性阈值, 且对目标项目有评分的用户加入近邻用户组, 如果近邻个数不足k个, 则选择相似性最高的用户作为补充, 而新补充的用户对目标项目的评分为用户评分均值整数部分。 图1 不同近邻选择策略下算法的性能 以上4种策略对应不同的协同过滤算法, 由于ST-1,ST-2和ST-4都受参数k的影响, 因此, 实验中比较了在不同k值下算法的性能。实验中k的取值分别为10,20,30,40,80,β的取值在数据集movielens上为[10,20]效果最优, 因此, 选取10,SsimT值在本实验中取0.45时效果最优, 实验结果如图1所示。 通过实验可以看出, 近邻选择策略对算法性能的影响较大, 使用近邻选择策略ST-4, 算法的EMAE值最小, 即笔者提出的算法DT-UBCF的性能最好。这是由于此时算法通过相似性阈值, 去除了相关性不强的近邻用户对预测结果的影响, 同时为了保证有尽量多的近邻参与计算, 又选择了对目标项目没有评分信息, 但与目标用户关联性较强的用户参与计算, 为了更详细地说明其中的变化, 表1给出了不同算法在性能最优情况下参考近邻比例和近邻用户组的平均相似度。 表1 不同算法的近邻用户组相似度(SNsim)和参考近邻比例(RNeibr) 从表1可以看出, UBCF-2的SNsim值最低。这是由于此近邻选择策略选择那些对目标项目有评分的用户, 导致有些用户与目标用户相似性接近0, 或为负值, 从而拉动整体的平均相似度, 而其他3种策略都避免了此方法。从参考近邻比例这个指标看, UBCF-1的值最低。虽然算法以全局最优的用户最为近邻, 但这些近邻并非都对目标项目有评分信息, DT-UBCF在考虑相似性的同时, 还考虑了近邻用户对目标项目的评分信息, 因此其各个指标都能达到一个不错的值, 算法的最终性能较好。 基于项目的协同过滤算法思想与基于用户的协同过滤相似, 因此, 只给出了DT-IBCF与传统IBCF在不同k值下算法性能的比较, 与其他算法的对比实验结果没有列出。图2为不同k值下IBCF算法推荐精度对比。从图2中可以看出, 改进后的算法推荐精度当近邻个数大于等于60时也有很大的提高。 图2 不同k值下IBCF算法推荐精度对比 从图2中推荐精度的趋势也可以看出, 当近邻个数大于100时, IBCF-1和IBCF-2算法的EMAE值趋于平缓状态, 因为满足条件的近邻数量是有限的, 即使要求的近邻个数再多, 也不能从稀疏的用户项目评分矩阵中找出满足数量的近邻。而DT-IBCF算法在近邻个数较少的情况下, 算法推荐精度不如IBCF-2, 是由于在开始的相似度阈值筛选过程中, 把目标用户有评分的项目但与目标项目相关度不算很强的项目排除在外了, 而引入了大量的与目标项目相关, 而目标用户并没有评分信息的项目, 增大了误差, 从而导致算法的EMAE值过低。 笔者提出了近邻组相似度和参考近邻比例两个指标, 用以评估协同过滤算法选出的近邻用户组或近邻项目组的质量, 通过这些指标从量化的角度揭示了传统协同过滤算法的不足, 并提出了双重阈值近邻查找法, 以发掘与目标用户或项目相关, 且能参与到最终预测评分计算的候选项目或用户, 充分利用现有稀疏的用户评分矩阵信息。并将此策略应用于基于近邻的协同过滤算法中, 通过实验分析, 可以看出, 该方法可有效提高推荐系统的推荐精度。对实际商业应用有一定参考价值。 参考文献: [1]GLODBCRG D, NICHOLS D, OKI B M, et al. Using Collaborative Filtering to Weave an Information Tapcstry [J]. Communication of the ACM, 1992, 35(12): 61-70. [2]NADAV GOLBANDI, YEHUDA KOREN, RONNY LEMPEL. Adaptive Bootstrapping of Recommender Systems Using Decision Trees [C]∥Proceeding of the Forth ACM International Conference on Web Search and Data Mining. New York, USA: ACM, 2011: 595-604. [3]GEORGE KARYPIS. Evaluation of Item-Based Top-N Recommendation Algorithms [C]∥CIKM’01: Proceedings of the Theth International Conference on Information and Knowledge Management. New York, USA: ACM, 2001: 247-254. [4]YUE SHI, MARTHA LARSON, ALAN HANJALIC. Exploiting User Similarity Based on Rated-Item Pools for Imprrved User-Based Collaborative Filtering [C]∥RecSys’09: Proceedings of the third ACM Conference on Recommender Systems. New York, USA: ACM, 2009: 125-132. [5]SARWAR B, KARYPIS G, KONSTAN J, et al. Application of Dimensionality Reduction in Recommender System: A Case Study [C]∥Proceeding of the ACM Web KDD Workshop on Web Mining for E Commerce. New York, USA: ACM, 2000: 82-90. [6]PREM MELVILLE, RAYMOND J MOONEY, RAMADASS NAGARAJAN. Content-Boosted Collaborative Filtering for Improved Recommendations [C]∥Proceedings of the Eighteenth National Conference on Artificial Intelligence(AAAI-2002). Edmonton, Canada: American Association for Artificial Intelligence, 2002: 187-192. [7]KOHRS A, MERIALDO B. Creating User-Adapted Websites by the Use of Collaborative Filtering [J]. Interacting with Computers, 2001, 13(6): 695-716. [8]SARWAR B M. Sparsity, Scalability and Distribution in Recommender System [D]. Minncapolis, MN: University of Minnesota, 2001. [9]ZHANG Ji-yong, PEARL PU. A Recursive Prediction Algorithm for Collaborative Filtering Recommender Systems [C]∥Proceedings of ACM Conference on Recommender Systems. [S.l.]: ACM, 2007: 57-64. [10]HERLOCKER J, KONSTAN J A, RIEDL J. An Empirical Analysis of Design Choices in Neigborhood-Based Collaborative Filtering Algorithms [J]. Information Retrieval, 2002, 5(4): 287-310. [11]HERLOCKER J L, KONSTAN J A, BORCHERS A, et al. An Algorithmic Framework for Performing Collaborative Filtering [C]∥Proceding of ACM SIGIR’99. [S.l.]: ACM, 1999: 230-237. [12]SARWAR B, KARYPIS G, KONSTAN J, et al. Item-Based Collaborative Filtering Recommendation Algorithms [C]∥Proceeding 10thInt, Conference on World Wide Web. New York, USA: ACM, 2001: 285-295. [13]SYMENOIDIS P, NANOPOULOS A, PAPADOPOULOS A N, et al. Collaborative Filtering: Fallacies and Insights in Measuring Similarity [C]∥Proceddings of the 10th PKDD Workshop on Web Mining(WEBMine 2006). Berlin, Germany: [s.n.], 2006: 56-67.2.3 双重阈值的基于用户的协同过滤算法
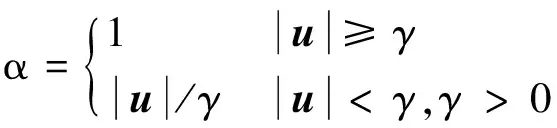

3 实 验
3.1 实验方法
3.2 评估指标
3.3 实验结果与分析


4 结 语
