基于非负矩阵分解的阴影检测方法
2013-10-15周鹏宇周大可
周鹏宇, 杨 欣, 周大可, 刘 加
(南京航空航天大学 自动化学院, 南京 210016)
0 引 言
在计算机视觉领域中, 阴影的存在往往对后续研究产生不利影响。阴影不仅影响人们视觉判读效果, 而且在诸如图像匹配研究中, 将直接影响图像匹配精度。
近年来, 关于阴影检测算法的研究有很多。这些算法大致可以分为两类: 基于模型方法和基于阴影特征方法。基于模型方法假定目标的三维几何结构和光源已知, 而后通过模型计算阴影形状和位置。该方法适用于某些较简单的特定场合, 主要原因在于其存在以下两方面不足[1]: 首先, 对于形状复杂物体, 建立模型十分困难; 其次, 该方法需要的光源和目标三维形状的先验知识难以得到。
基于阴影特征方法是依据阴影区域亮度、 颜色和几何特征实现阴影检测[2-7]。如, 文献[2]在3维RGB空间中设计了计算颜色模型, 通过此模型分离色度和亮度两个分量, 再通过对比前景和背景对应像素点的这两个分量实现阴影检测; 文献[3]中将3个颜色分量看成多光谱影像的3个波段, 而后使用K-L变换, 最终通过分类特性检测阴影; 文献[4]先把RGB图像转化为HSI图像, 而后通过比对前景与背景对应点H、S、I3个分量检测阴影。基于阴影特征方法与基于模型方法相比, 具有更广泛的适用性。目前, 大部分研究都属于第2种方法, 笔者所用方法也属于此类。
非负矩阵分解(NMF: Non-negative Matrix Factorization)是一种新矩阵分解算法, 与传统的矩阵分解方法相比, 该方法能保证分解结果不含负值, 更适用于解决实际问题, 目前已被应用于图像识别领域[8-10]。如, 在文献[8]中使用NMF算法进行人脸识别, 并对比了3种NMF算法的识别效果; 文献[9]中对原有NMF算法进行改进, 通过余弦相似分类器和最大相关分类器实现人脸识别。
虽然NMF算法在模式识别方面具有较好应用前景, 但目前其在阴影检测方面应用并不多见。笔者正是针对这一情况, 详细研究在HSI空间中使用NMF以及BNMF(Block Non-negative Matrix Factorization )进行阴影检测, 提出了完整的基于NMF和BNMF的阴影检测算法。实验结果表明, 该方法能有效地检测阴影区域。
1 基于NMF的阴影检测
1.1 NMF基本原理
NMF算法由Lee等[11]于1999年提出, 其基本思想描述如下。
对于任意给定的m×n非负矩阵X, 通过NMF算法能找到m×r矩阵W(非负)和r×n矩阵H(非负), 使
Xm×n≈Wm×rHr×n
(1)
其中r一般满足r Xj≈h1,jW1+h2,jW2+…+hr,jWr (2) NMF算法的一般实现过程如下。 首先, 随机生成基矩阵W(m×r)和系数矩阵H(r×n);而后, 计算WH与原矩阵X的误差, 如果误差不满足要求, 则不断更新W与H中元素, 直至满足要求为止。矩阵W与矩阵H的更新方式如下。 更新H一行元素 (3) 更新W相应的一列元素 (4) 非负矩阵分解是一种新矩阵分解方法, 与传统的矩阵分解方法(如奇异值分解等)相比, NMF能保证分解结果一定是非负的。从数学角度看, 分解结果存在负值是合理的。但在实际问题中, 负值元素往往没有意义。例如, 在图像中, 不存在负值的像素点; 在文档统计中, 负值也无法解释。基于以上原因, 考虑到目前还没有关于NMF的阴影检测研究, 笔者给出了基于NMF的阴影检测方法。 阴影检测可看成是一种识别问题, 只要识别出阴影所在区域便可实现阴影检测。基于NMF的识别步骤如下。 4) 使用分类准则, 确定x的类属C(x), 即当j=arg ming(x,Li)时,C(x)=j。 使用上述算法前, 必须考虑阴影区范围的确定、 参数r以及判别函数的选取问题。在通常情况下, 阴影点与非阴影点的区分都是依据亮度、 颜色等特征。这些特征在经过NMF分解后, 最终都是通过W、H两个矩阵体现。然而, 由于矩阵W(m×r)和矩阵H(r×n)维数与原矩阵维数(m×n)不同, 如果不能对应原图像矩阵中阴影点的位置, 则进行分类是没有意义的。为此, 笔者提出了两种解决方案。 方法1通过公式 (5) 找出W、H和X矩阵坐标的对应关系。 式(5)是以式(2)为基础推导得出的。分析式(5)可以看出,H中的一列元素结合W的一行元素才能确定一个点。此外, 由于一幅图像中像素点非常多, 如果每个点都通过式(5)定位, 算法非常复杂。鉴于上述原因, 笔者采用了第2种方法。 方法2是先将图像矩阵分解为若干大小相同的小块, 而后分别对每小块进行NMF分解。分解后判别类属, 对应的矩阵块就划分为阴影区或非阴影区。第2种方法的难点在于将原矩阵分解为尺寸合适的小块, 如果矩阵小块尺寸偏大, 则检测误差变大。如果尺寸偏小, 则会使计算量变大。在该研究中, 为更好地解决该问题, 考虑将原矩阵分解为8×8的小块。这样做的目的在于8×8的小块可以继续细分解为4×4或2×2的矩阵块。在实验时, 首先使用NMF或BNMF对8×8的小块进行阴影检测。而后, 对于误差较大或暂时不能确定类别的矩阵块, 可将其细分为4×4或2×2的矩阵块后继续使用NMF或BNMF分类。 对于参数r的选取问题, 目前的研究还没有给出较好的方法。r值的大小反映了特征子空间的维数, 当r与实际数据集特征空间的维数基本一致时, 得到的NMF特征子空间对数据的夹逼性最好。笔者仿真时选用了多个r值, 而后根据结果选出最适合的r。 由于采用基于NMF的阴影检测, 因此, 实验所用判别函数融合了NMF的特点, 即 (6) NMF算法的分解结果都是非负的, 因此不同类别系数矩阵的列向量必然不是正交的。在这种情况下, 由于不能消除不同类别间的相关性, 检测结果必然会受到影响。此外, NMF算法在训练样本或类别增加时要重复学习。上述的两个方面, 限制了NMF的实际应用。笔者针对这些不足, 引入了分块非负矩阵分解算法。BNMF算法属于非负矩阵分解的改进型, 其基本思想如下。 首先, 将一个大矩阵按类别分成若干块; 而后, 对每块小矩阵进行NMF分解, 进而得到各自的基矩阵与系数矩阵; 最后, 将各类基矩阵和系数矩阵进行合成, 得到总的基矩阵与系数矩阵。 假设共有C类样本, 每类样本维数为m×n0,xi为第i类样本(i=1,2,…,C)。如果有(xi)m×n0≈(Wi)m×r0(Hi)r0×n0, 则BNMF分解结果可以表示为 (7) BNMF分解结果的形式特殊, 如果需要加入新的训练样本或是新的类别, 可按照如下规则。 (8) (9) 分析式(7)可看出, BNMF分解结果包含所有类别的基矩阵和系数矩阵, 由于总的系数矩阵是由各类系数矩阵对角构成。因此, 各类系数矩阵列向量相互正交, 能消除不同类别间的相关性, 进而能提高阴影区和非阴影区的识别效果。式(8)和式(9)也表明BNMF算法能方便地实现增量的学习。更多关于BNMF的内容可以参考文献[13]。 使用BNMF检测阴影前, 同样要考虑阴影区范围的确定、 参数r以及判别函数的选取问题。前两个问题的解决方法与NMF算法相同, 但由于BNMF形式特殊, 式(6)所示改进判别函数不再适用。基于BNMF的阴影检测算法的详细过程如下: 1) 抽取阴影区和非阴影区两类训练样本, 每类训练样本写成矩阵形式, 即(Xi)m×n0,i=1,2; 2) 使用NMF分解每个(Xi)m×n0, 求出各自的Wi矩阵与Hi矩阵; h=W+x=(WTW)-1WTx (10) 图1 原图 笔者采用基于阴影特征的阴影检测方法, 先将RGB图像转化为HSI图像, 再根据图像的I分量判定是否为阴影。实验选用一段交通视频中的第150帧图像进行算法验证, 为了便于图像矩阵分块, 将原图尺寸调整为200×320(见图1)。由于进行NMF分解时需要初始化基矩阵W和系数矩阵H, 为减弱不同初始值对算法的影响, 每组实验都重复进行5次。NMF算法和BNMF算法的迭代次数都设为100次。 具体实验过程如下: 1) 原图像转化为HSI图像, 将图像中的I分量矩阵从第1行第1列开始, 按8×8依次分块(I范围转换为0~255), 分块结果作为测试样本; 2) 抽取尺寸为8×8的阴影、 非阴影两类训练样本, 通过NMF或BNMF求取各个类别的基矩阵和系数矩阵(r=5); 3) 以各类别的基矩阵为特征基, 求出特征基对应的系数矩阵; 4) 设定阈值, 根据判别函数分类, 并标记已分类别的部分, 不能确定类别的部分细分为4×4(r=3)或2×2(r=2)的矩阵块继续使用NMF或BNMF分类。 a 第1次分类结果 b 最终分类结果 a 第1次分类结果 b 最终分类结果 该实验分别采用NMF算法和BNMF算法检测阴影, 实验时两种算法选用的判别函数类型相同, 都是通过计算测试样本与训练样本系数矩阵间的欧氏距离判定阴影。实验结果如图4和图2所示。 a 第1次分类结果 b 最终分类结果 比较图4a和图2a可看出, 在判别函数类型相同的情况下, NMF算法第1次分类阴影区误差大于BNMF算法第1次分类结果。从图4b和图2b中阴影的形状可看出, BNMF的检测细节要好于NMF的最终结果。在进行实验时, BNMF算法的复杂度比NMF算法小, 文献[13]中通过对比NMF与BNMF复杂度也证实了此结论。此外, 分析式(7)可看出, 各类别系数矩阵形成的H矩阵, 其列向量相互正交, BNMF能消除不同类别间的相关性。因此, 与传统的NMF相比, 在判别函数类型相同的情况下, BNMF的效果更佳。 图5所示为4种方法的检测结果[14], 通过在HSV空间利用阴影区域亮度和色调的特点, 可得到如图5a所示结果。对比图5中阴影形状以及道路中白线的消除可得出以下结论: 1) BNMF算法虽然存在一些误差, 但与前两种方法相比, 检测细节更清晰; 2) 改进判别函数后, NMF算法检测结果与前两个结果相比, 更加清晰, 效果较好; 3) 在判别函数类型相同的情况下, BNMF检测结果好于NMF的结果。 a 文献[14] b 奇异值分解 c NMF判别函数1 d NMF判别函数2 e BNMF 由此可见, 与其他矩阵分解方法相比, 非负矩阵分解由于其自身的特点, 更加贴近实际应用。 笔者使用NMF算法实现了阴影检测, 讨论了不同判别函数对检测结果的影响, 对比了NMF算法和BNMF算法的两种阴影检测效果。实验结果表明, NMF算法和BNMF算法均能有效检测阴影区域, 但BNMF算法较NMF算法步骤少, 细节更清晰。今后的研究工作将主要集中于判别函数的改进以及其他改进非负矩阵分解方法的应用。 参考文献: [1]陈柏生, 陈锻生. 基于归一化RGB彩色模型的运动阴影检测 [J]. 计算机应用, 2006, 26(8): 1879-1881. CHEN Bai-sheng, CHEN Duan-sheng. Normalized RGB Color Model Based Shadow Detection [J]. Computer Applications, 2006, 26(8): 1879-1881. [2]郭建波, 周剑利, 韩鸿哲, 等. 背景差法中的阴影消除方法 [J]. 辽宁工程技术大学学报, 2005, 24(1): 104-106. GUO Jian-bo, ZHOU Jian-li, HAN Hong-zhe, et al. Shadow Suppression Method for Background Subtraction [J]. Journal of Liaoning Technical University, 2005, 24(1): 104-106. [3]王树根, 王军利, 郭丽艳. 基于K-L变换的彩色航空影像阴影检测 [J]. 测绘信息与工程, 2004, 29(2): 21-22. WANG Shu-gen, WANG Jun-li, GUO Li-yan. Shadow Detection of Color Aerial Images Based on K-L Transformation [J]. Journal of Geomatics, 2004, 29(2): 21-22. [4]潘翔. 基于彩色信息和边缘特征的运动阴影检测 [J]. 浙江大学学报, 2004, 38(4): 389-391. PAN Xiang. Moving Shadow Detection Based on Color Information and Edge Features [J]. Journal of Zhejiang University, 2004, 38(4): 389-391. [5]乔振民, 邢立新, 李淼淼, 等. 遥感影像的云及其阴影覆盖区光谱重构 [J]. 吉林大学学报: 信息科学版, 2012, 30(1): 35-39. QIAO Zhen-min, XING Li-xin, LI Miao-miao, et al. Spectral Reconstruction of Remote Sensing Image’s Clouds and Its Shadow Coverage [J]. Journal of Jilin University: Information Science Edition, 2012, 30(1): 35-39. [6]李子龙, 刘伟铭. 基于组合特征和HSI颜色空间的阴影检测 [J]. 微电子学与计算机, 2011, 28(3): 66-69. LI Zi-long, LIU Wei-ming. Shadow Detection Based on Mixed Feature and HSI Color Space [J]. Microelectronics & Computer, 2011, 28(3): 66-69. [7]董蓉, 李勃, 陈启美. 路况视频中HSV彩色不变量阴影检测法研究与改进 [J]. 中国图像图形学报, 2009, 14(12): 2483-2488. DONG Rong, LI Bo, CHEN Qi-mei. Research and Improvement on Shadow Detectionin Expressway Videos Using HSV Color Model [J]. Journal of Image and Graphics, 2009, 14(12): 2483-2488. [8]郭建虎. 非负矩阵分解方法及其在人脸识别中的应用 [D]. 兰州: 兰州理工大学计算机与通信学院, 2010. GUO Jian-hu. Non-Negative Matrix Factorization and Its Applications to Face Recognition [D]. Lanzhou: School of Computer and Communication, Lanzhou University of Technology, 2010. [9]李勇智, 杨静宇. 基于非负矩阵分解新的人脸识别方法 [J]. 系统仿真学报, 2008, 20(1): 111-116. LI Yong-zhi, YANG Jing-yu. Novel Methods of Face Recognition Based on Non-Negative Matrix Factorization [J]. Journal of System Simulation, 2008, 20(1): 111-116. [10]郝红. 非负矩阵分解在遥感图像识别中的应用 [D]. 杭州: 浙江农林大学环境与资源学院, 2011. HAO Hong. Application of Non-Negative Matrix Factorization Method in Remote Sensing Image Recognition [D]. Hangzhou: School of Environmental and Resource Sciences, Zhejiang A & F University, 2011. [11]LEE D D, SEUNG H S. Learning the Parts of Objects by Non-Negative Matrix Factorization [J]. Nature, 1999, 401(6755): 788-791. [12]赵玲. 基于独立分量分析和非负矩阵分解的人脸识别研究 [D]. 兰州: 兰州大学信息学院, 2006. ZHAO Ling. Face Recognition Studying Based on ICA and NMF [D]. Lanzhou: School of Information Science & Engineering, Lanzhou University, 2006. [13]潘杉杉, 陈文胜, 徐晨. 基于分块非负矩阵分解人脸识别增量学习 [J]. 计算机应用研究, 2009, 26(1): 117-120. PAN Shan-shan, CHEN Wen-sheng, XU Chen. Incremental Learning of Face Recognition Based on Block Non-Negative Matrix Factorization [J]. Application Research of Computer, 2009, 26(1): 117-120. [14]陈柏生. HSV彩色空间的室内外运动人检测与阴影消除 [J]. 华侨大学学报, 2007, 28(1): 30-33. CHEN Bai-sheng. Indoor and Outdoor People Detection and Shadow Elimination by Exploiting HSV Color Information [J]. Journal of Huaqiao University, 2007,28(1): 30-33.1.2 基于NMF的阴影检测算法

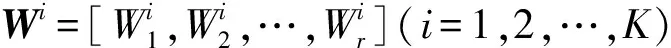

1.3 阴影区范围的确定
1.4 参数r以及判别函数的选取

2 基于分块非负矩阵分解的阴影检测
2.1 分块非负矩阵分解
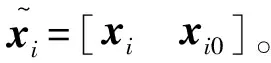

2.2 基于BNMF的阴影检测算法
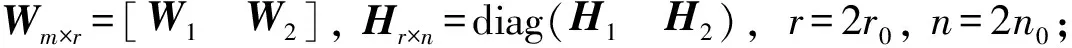


3 实验与分析

3.1 实验1



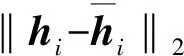
3.2 实验2



4 结 语
