基于HFE公钥密码的单向壳核函数构造方案

王 芳, 袁 哲

(白城师范学院 传媒学院, 吉林 白城 137000； 吉林大学 机械科学与工程学院, 长春 130022)

0 引 言

公钥密码是信息安全和可信计算的精髓和核心。到目前为止, 已经提出了很多种不同的公钥密码体制, 其可分成两大类： 1) 基于大整数因子分解的公钥密码, 如RSA公钥密码体制； 2) 基于离散对数问题的公钥密码, 如ECC(Error Correcting Code)公钥密码体制。随着科技的进步, 量子计算机的出现对RSA和ECC公钥密码构成了巨大威胁。因此, 急需寻找一种新的公钥密码替代这些安全性受到威胁的公钥密码[1-4]。

随着密码技术的快速发展, 20世纪数学将成为下一代公钥密码的坚实基础。有限域中的多变元二次方程组问题(MQ: Multivariate Quadratic)是被广泛认可的一种替代方案。目前人们已经研究出了一些基于MQ问题比较成型的方案, 其中主要方案有隐藏域方程(HFE: Hidden Field Equations)、 UOV(Unbalanced Oil and Vinegar Scheme)、 STS (Stepwise Triangular Systems)、 MIC*(Matsumoto-Imai Scheme)、 ιIC(ι-Invertible Cycles)。虽然有人经过深入研究, 提出了一些对MQ问题的攻击方案[1], 但人们针对这些攻击方案, 已将这些基本方案进行了变形, 如(HFEv-)、 STS(UOV)、 (ιICi+)等[5,6]。

基于MQ问题的公钥密码具有较好的发展前景, 具有加密速度和验证签名速度快, 抵御量子攻击潜力大等优点。笔者借鉴了HFE公钥密码的设计思想[7-13], 构造出一种应用灵活, 安全性更高的函数, 即单向壳核函数。

1 HFE公钥密码原理

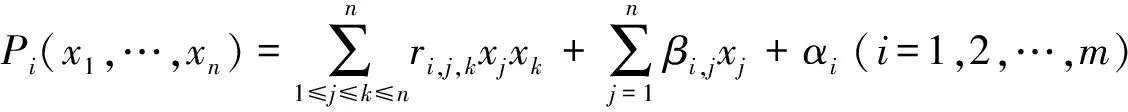
此求解问题是基于解有限域上的MQ问题, 是NP困难问题[5-13]。HFE公钥密码体制正属于这样的MQ问题, 其加密/解密过程如图1所示。

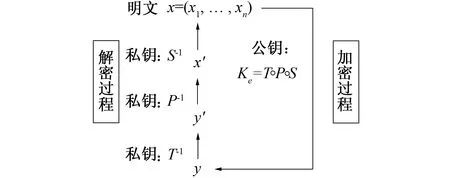
图1 HFE公钥密码加密/解密过程

1) 确定参数。① 确定基本有限域Fq和元组n； ② 构造的可逆线性变换S, 可逆非线性变换P以及可逆线性变换T； ③ 根据第②步所得, 计算公钥Kθ=T∘P∘S, 用于加密； ④ 把S、P、T的逆函数(S-1,P-1,T-1)作为私钥Kd, 用于解密。

2) 加密过程。利用公钥Kθ, 加密明文x, 得到密文y=EKθ(x)=T(P(S(x)))。

3) 解密过程。利用私钥Kd, 解密所得的密文y, 对密文先做T-1(y)运算, 然后做P-1(T-1(y))运算, 最后做S-1(P-1(T-1(y)))得到明文x。

2 单向壳核函数的构造

2.1 单向壳核函数的引入

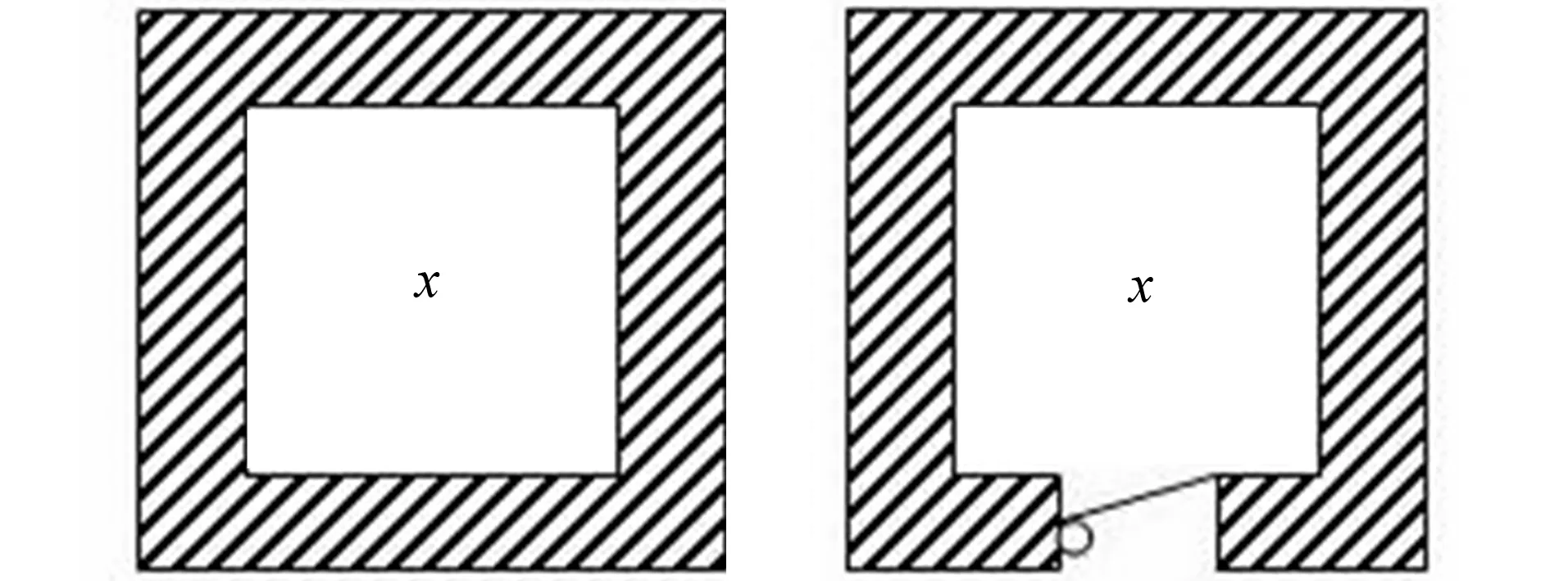
图2 单向函数结构 图3 单向陷门函数结构

由单向函数的定义可知, 当x已知时, 计算y=f(x)非常容易, 而当y已知, 求解x满足y=f(x), 则非常困难。所以, 单向函数类似于将已知的x放入封闭的盒子里(见图2)。

已知陷门k的条件下, 求解x, 使y=f(x)是非常容易的。由此可见, 单向陷门函数类似于将已知的x放入到带有暗门的盒子里(见图3)。

结合单向函数及单向陷门函数各自的结构特点, 笔者提出了一种特点更鲜明的单向壳核函数, 这种函数的两种结构如图4所示。

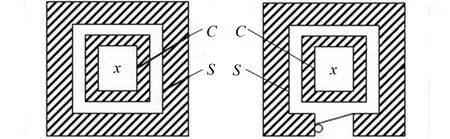
a 第1种结构 b 第2种结构

图4引入了壳函数S、 核函数C、 剥壳函数S-1与剥核函数C-1。其中, 单向壳核函数SC(x)=S∘C(x)=S(C(x)), 即壳函数S及核函数C二者的复合计算。

2.2 基于HFE公钥密码体制的构造方案

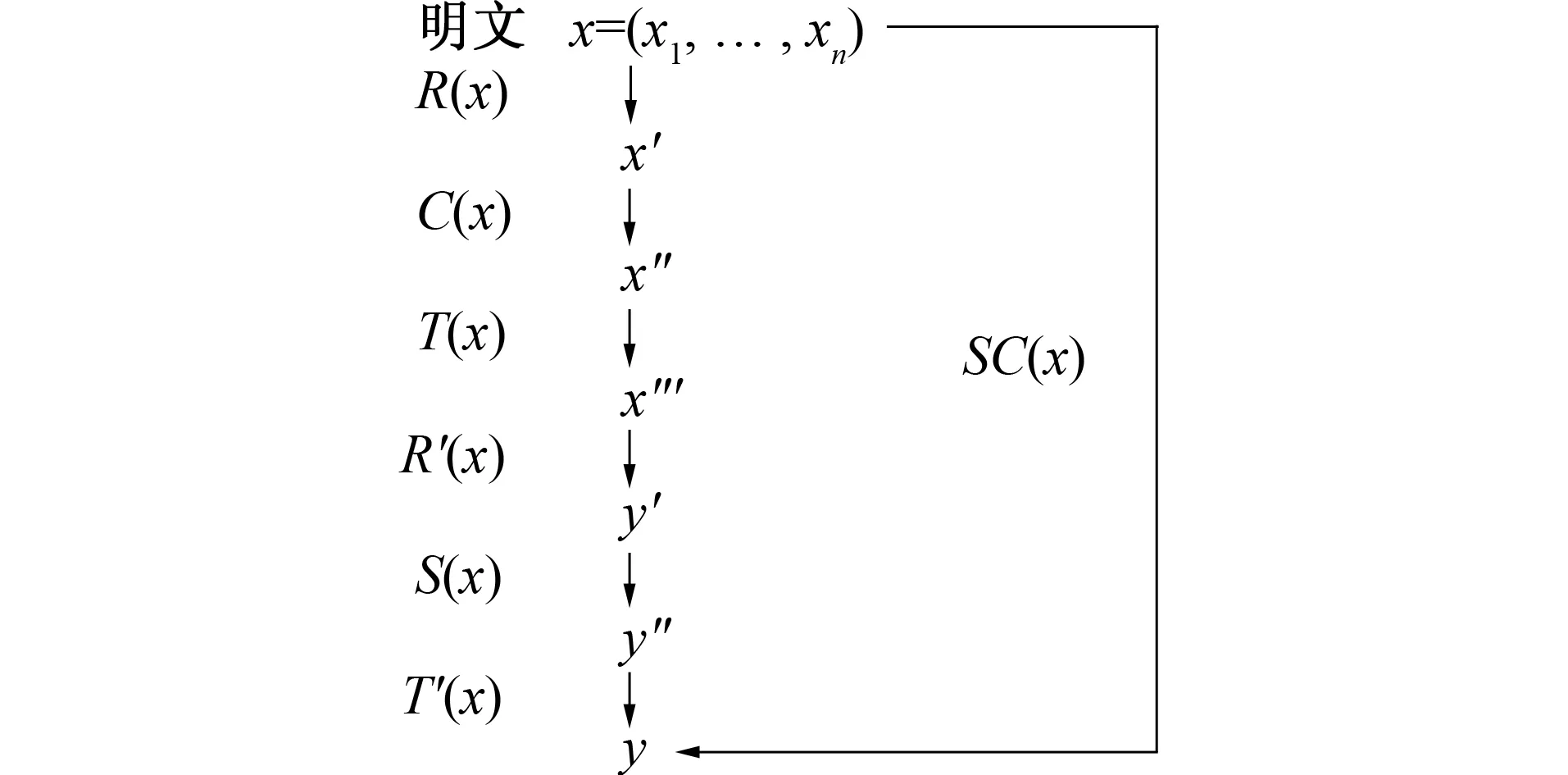
图5 基于HFE思想所构造的单向壳核函数的原理图

单向壳核函数的概念以及两种结构已经被引入, 下面将利用HFE公钥密码的设计思想构造单向壳核函数的第1种结构, 即壳函数S与核函数C同为单向函数。基于HFE公钥密码所构造的单向壳核函数的原理如图5所示。

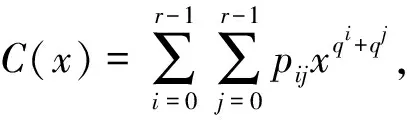
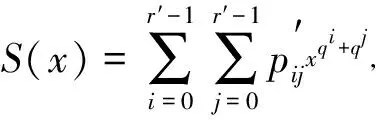
壳函数S和核函数C具有相同的构造形式, 类似于HFE公钥密码变换过程中的函数P(x)。它们的相同点是： 具有相似的结构, 又都是在F的扩展域E上进行运算。不同点是： HFE中的P(x)是可逆变换, 为了确保P(x)可逆, 其中常数r不能太大； 而单向壳核函数中的壳函数S与核函数C都是单向函数, 无需满足可逆性, 其中常数r可以很大。

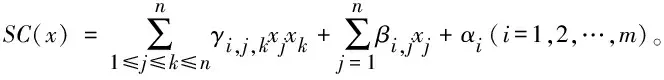
2.3 安全分析

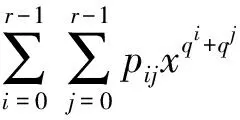
1) GB方法与XL方法。由于XL方法可以看成是GB方法的一个特例, 只需说明单向壳核函数可以抵抗GB攻击即可。对于随机选取的MQ方程组, 当m≤n时, 计算GB时所产生的中间多项式的次数往往增长快速, 为O(2n)。所以, 当n取值较大时, 此类算法在空间和时间上不可行。当选取的单向壳核函数的MQ方程组具有真随机性, 在m≤n时, 计算GB时所产生的中间多项式的次数增长快速, 当n取值很大时, 此类算法在空间和时间上不可行。单向壳核函数的壳函数S(x)和核函数C(x)是单向不可逆的, 导致多项式的次数会很大。因此, GB方法与XL方法对单向壳核函数无法进行有效的攻击。

2) 重线性化方法。重线性化次数的增大, 导致线性相关方程数量也在迅速增加, 且这种方法仅适用于超定义的MQ方程组。对于HFE公钥密码的攻击, 重线性化方法主要利用P(x)变换的可逆性(常数r不能太大)这个弱点进行攻击的。这种攻击方法对HFE的攻击有效, 但对单向壳核函数却毫无作用。因为单向壳核函数的壳函数S(x)与核函数C(x)都为单向函数, 不可逆, 要求r很大。但r的不断增大, 导致线性相关的方程数量迅速增长, 次数也随之变大。因此, 重线性化方法对单向壳核函数无法进行有效的攻击。

3) DR方法。DR方法只是对E(x1,…,xn)稀疏时有效, 否则Dixon矩阵的尺寸至少为O(2n), 易知DR方法对于求解一般MQ方程组的实际意义不大。在选取单向壳核函数的MQ方程组时, 可以选择具有真随机性的MQ方程组。因此, DR方法对单向壳核函数无法进行有效攻击。

4) 指定变元法。假如q较小, 则可任意给定r个变元, 使m>(n-r), 倘若m个方程和n-r个变元的MQ问题可解, 可以用GB、 XL等方法求解。但由于可选具有真随机性的单向壳核函数MQ方程组, 函数具有单向性的特征, 指定变元法对单向壳核函数的攻击仍然无用。

3 结 语

笔者引入了单向壳核函数公钥密码体制, 根据HFE公钥密码的设计思想, 构造了单向壳核函数, 并给予了安全性分析, 证明了该新型的公钥密码具有很强的安全性。单向壳核函数的提出, 给出了一种新型的公钥密码体制, 经过深入研究, 将会具有更广阔的应用前景。

参考文献：

[1]WILLIAM STALLINGS. 密码编码学与网络安全原理与实践 [M]. 北京: 电子工业出版社, 2001.

WILLIAM STALLINGS. Cryptography and Network Security Principles and Practice [M]. Beijing: Publishing House of Electronic Industry, 2001.

[2]曹珍富. 公钥密码学 [M]. 哈尔滨: 黑龙江教育出版社, 1993.

CAO Zhen-fu. Public Key Cryptography [M]. Harbin: Heilongjiang Education Press, 1993.

[3]袁哲, 赵永哲, 张文睿, 等. 敏感数据安全传输方法 [J]. 吉林工程技术师范学院学报, 2008, 24(1): 73-77.

YUAN Zhe, ZHAO Yong-zhe, ZHANG Wen-rui, et al. Sensitive Data Secure Transmission Methods [J]. Jilin Engineering and Technical Teachers College, 2008, 24(1): 73-77.

[4]袁哲, 赵永哲, 李光伟, 等. 利用有限域上遍历矩阵实现基于隐藏基的密钥交换 [J]. 吉林大学学报: 理学版, 2009, 47(4): 783-789.

YUAN Zhe, ZHAO Yong-zhe, LI Guang-wei, et al. Finite Fields Hidden Base Ergodic Matrix-Based Key Exchange [J]. Journal of Jilin University: Science Edition, 2009, 47 (4): 783-789.

[5]CHRISTOPHER WOLF. Hidden Field Equations (HFE)-Variations and Attacks [EB/OL]. [2013-04-15]. http://www.christopher-wolf.de/dpl, 2003.

[6]NICOLAS COURTOIS. The HFE Public Key Encryption and Signature [EB/OL]. [2013-04-15]. http://www.minran K.org/hfe/, 2005.

[7]NICOLAS COURTOIS. The Security of Hidden Field Equations (HFE) [C]∥Cryptographers’ Track RSA Conf, LNCS 2020. Berlin: Spring Verlag, 2001: 266-281.

[8]FELL H, DIFFIE W. Analysis of a Public Key Approach Based on Polynomial Substitution [C]∥Crypto’85, LNCS 218. Berlin: Spring Verlag, 1985: 340-349.

[9]LOUIS GOUBIN, JACQUES PARTARIN. Trapdoor One-Way Permutations and Multivariate Polynomials [C]∥ISICS’97, LNCS 1334. Berlin: Spring Verlag, 1997: 356-368.

[10]JACQUES PARTARIN. Hidden Field Equations (HFE) and Isomorphism of Polynomial (IP): Two New Families of Asymmetric Algorithms [C]∥EuropCrypt’96, LNCS1070. Berlin: Spring Verlag, 1996: 33-48.

[11]AVIAD KIPNIS, ADI SHAMIR. Cryptanalysis of the HFE Public Key Cryptosystem [C]∥Crypto’99, LNCS 1666. Berlin: Spring Verlag, 1999: 19-30.

[12]陈辉焱, 王连强, 吕述望. 关于HFE密码系统的密钥问题研究 [J]. 计算机研究与发展, 2007, 44(7): 1205-1210.

CHEN Hui-yan, WANG Lian-qiang, LÜ Shu-wang. About HFE Key Cryptography Research [J]. Computer Research and Development, 2007, 44(7): 1205-1210.

[13]杨敏, 孟庆树, 张焕国. 基于ECC和HFE的纠错密码构造 [J]. 计算机工程与应用, 2008, 44(27): 31-32.

YANG Min, MENG Qing-shu, ZHANG Huan-guo. HFE-Based Error Correction Code ECC and Construction [J]. Computer Engineering and Applications, 2008, 44(27): 31-32.