由粗到精的三维人脸稀疏重建方法

吴子扬, 周大可, 杨 欣, 胡阳明

(南京航空航天大学 自动化学院, 南京 210016)

0 引 言

近年来, 由于计算机图形学和模式识别理论的不断发展, 基于人脸面部的应用越来越受到关注。随着人脸检测、 人脸识别等应用日益商业化, 人们开始认识到以图片形式表达的人脸信息在实际处理中普遍受到光照、 姿态等多方面的制约。因此, 对人脸计算机表达的相关研究也由传统的二维空间转向三维空间。由于直接获取人脸的三维数据需要昂贵的硬件, 故由人脸的二维图像恢复其三维信息普遍成为当前研究的热点[1]。

由面部图像恢复三维信息的经典方法是Blanz等[2,3]和Patel等[4]提出的形变模型算法, 通过对一系列的三维人脸样本进行统计计算参考人脸, 求解全局优化方程实现参考人脸到待重建样本的匹配, 其本质是线性组合思想, 即通过某一子空间的基表达该空间的具体实例。由于形变模型方法需要通过迭代求得全局最优解, 故需要在局部细节和重建速度上做出一定的牺牲, 王成章等[5]提出了利用改进的遗传算法求解形变因子, 在形变模型的基础上节省了11 min以上。Blanz等[6]和胡阳明等[7]提出了通过少量特征点重建三维模型的方法, 即稀疏形变模型法。稀疏形变模型同样利用线性组合思想, 通过对面部少量特征点近似求解优化方程, 得到形变系数, 从而完成参考模型的形变。其优势在于重建速度快, 且重建精度不会损失太多。后续的工作主要建立在统计得到的参考模型[8-10]之上, 通过不同方法对参考模型进行形变或修改以得到最终重建结果。

Liao等[11]将局部形变模型与明暗恢复(SFS: Shadow From Shading)方法结合, 对人脸的局部区域分别重建, 通过RBF(Radical Basis Function)径向基插值得到最终结果。但由于局部形变模型较整体形变模型而言更易受到训练样本的影响, 且该方法需要首先在二维图像上检测出关键区域, 故统计得到每个区域的形变模型较困难。文献[12,13]提出通过参考模型和待重建人脸面部灰度值计算光照反射率, 通过迭代寻优的方法恢复整体的深度值, 但由于需要比较参考模型和待重建模型的灰度值, 该方法在很大程度上会受到光照条件的影响。为了解决单纯的稀疏形变模型对人脸模型细节描述能力不够[14]这一缺陷, 龚勋[15]提出了双形变模型方法, 即将两种弱形变模型结果通过加权方式结合得到最终三维重建结果。该方法对细节的表达较为丰富, 但不足在于权值的计算方法以及两种弱形变模型参数的确定。此外, 还有部分研究集中于对原始形变模型优化方程的改进[16,17]。

笔者在前述工作的基础上, 通过对稀疏形变模型的研究, 提出了一种由粗到精的重建方案, 即分步重建。首先通过对部分点的稀疏重建得到一个外形相似的粗略模型, 替代原有参考模型, 并将剩余点根据新的参考模型进行第2步重建。实验表明, 该方法在不降低重建速度的基础上能有效提高重建精度, 为三维人脸重建的研究提供一定的借鉴, 也为后续的三维人脸识别打下基础。

1 稀疏形变模型简介

将三维人脸子空间Rn视为线性子空间, 其中任意一个元素都可由其余元素线性表示, 即

(1)

通常情况下, 采集到的三维人脸数据由点云组成, 而每个三维人脸的形状信息也可用点云的坐标表示, 即Si=(x1,y1,z1,x2,y2,z2,…,xk,yk,zk)T, 其中k为点云的数目。如果直接使用所有三维人脸数据重构新的三维人脸的计算量巨大, 一般采用主成分分析(PCA: Principal Component Analysis)理论对样本数据库进行降维, 得到

(2)

根据式(2)可知, 求取β需要知道测试人脸三维模型上点云的坐标信息, 但实际测量对象是二维图片, 仅能获取二维人脸上若干点的位置信息。文献[6]给出了由少量二维点数据恢复整体三维人脸信息方法, 即稀疏形变模型理论。

设测量得到的二维稀疏坐标信息为d=(x1,y1,x2,y2,…,xl,yl)T∈R2l, 其中l为二维取点的数目。设该人脸三维模型全体点坐标数据D到二维稀疏点坐标的映射关系为L, 则d=LD, 根据式(2), 可做出以下推导

(3)

LΔS=Δd=LPβ=Pfβ

(4)

Δd=Pfβ

(5)

其中Δd为关键特征点的二维坐标与对应平均模型上三维点坐标投影的距离,Pf代表从主成分中选取对应特征点的二维坐标集合。通常, 直接采用式(5)计算β会带来过拟合现象, 故一般采用文献[6]所述基于贝叶斯最大后验概率的最优解法。令目标函数为

E(β)=‖Pfβ-Δd‖2+η‖β‖2

(6)

其中η为权重系数。根据奇异值分解(SVD: Sigular Value Decomposition), 有Pf=UΛVT, 其中Λ为特征值构成的对角矩阵,U由Pf(Pf)T的特征向量构成,V由(Pf)TPf的特征向量构成。这样可得其最优解为

(7)

将式(7)的计算结果带入式(2), 可得到三维数据的重建结果

(8)

图1给出扰动系数η变化对重建结果的影响。由图1可见,η越大, 重建结果越接近平均人脸, 误差越大；η过小会导致过匹配, 重建结果严重变形。

图1 扰动系数η对重建结果的影响

2 三维人脸稀疏分步重建

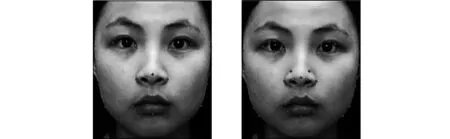
a 第1步重建特征点 b 所有特征点

用于测试的二维人脸首先需要进行特征点的定位, 并将定位后的二维坐标与三维平均人脸坐标建立对应关系。这种对应关系通常通过空间坐标系到平面坐标系的投影建立, 将二维坐标转换为图像坐标, 其原点一般取鼻尖点； 而将三维坐标转换为柱面坐标, 鼻尖点对应于三维坐标的(0,Ymax,0)。在实际操作中, 由于测试人脸受到光照不均或姿态不完全校正等影响, 无法准确定位出所有特征点, 特别是面部区域非显著点。根据式(7), 所有点的信息均需要带入运算才能求得最优形变因子, 如果存在定位不准确的点, 将导致求得的形变因子不准确。因此, 在传统的稀疏重建方法中, 二维面部每个特征点定位的精度都会直接影响重建结果的精度。

为克服一次重建存在的问题, 笔者采用三维人脸稀疏分步重建的方法。利用由粗到精的思路, 先根据面部定位较准确的关键特征点进行重建, 得到重建的粗略模型, 并根据第1步重建结果进行第2步重建。两步中选取的特征点如图2所示。

由式(8)可得到由上述特征点重建后的第1步重建结果

(9)

其中η1为第1步重建的扰动因子。

将S1作为第2步重建的参考人脸, 可得到其余特征点的二维坐标与新的参考人脸三维坐标投影的距离Δd′。在此基础上将Δd′带入式(6), 可得

(10)

其中η2为第2步重建的扰动因子。可以得到分步重建的最终结果

(11)

在第1步重建过程中, 选择每个区域的显著点, 如眼角、 鼻翼和嘴角点作为重建特征点, 以确定三维人脸的大体形状和各个区域的位置。由于选取的点较少, 一方面虽然重建出的模型细节表达不完善, 但能大体确定出待重建人脸的形状和区域的位置； 另一方面由于每个区域只选取显著的特征点, 避免了同一区域非显著点对显著点的干扰。在第2步重建过程中, 由于已得到了一个粗略的形状模型, 故需要选取较多的特征点对该模型进行形变, 以达到对模型细节的重建。

在两步重建的过程中, 扰动系数的选择也应采用不同的方式。第1步重建是为得到大体形状以及区域位置, 应选取较小的扰动系数以减小加入的干扰； 第2步重建是为得到较精确的模型, 应选取使重建结果误差较小的扰动系数。

笔者提出的分步重建算法流程如图3所示。

图3 分步重建算法流程

3 实验结果

实验以BJUT-3D Face Database中的部分三维人脸数据为训练样本, 测试样本为该库其余样本、 部分CAS-PEAL二维人脸数据库以及部分现实照片。实验采用的硬件环境为主频1.80 GHz的双核Intel CPU和2.0 GByte内存, 软件环境为Matlab 2012a和VC++6.0。

实验分为两部分。

1) 库内测试。训练样本和测试样本均来自BJUT-3D数据库, 选取已规范化(每个人脸由23 676个点构成)的70个三维人脸数据作为训练集, 30个三维人脸数据作为测试集。将测试集样本通过正交投影得到二维数据库, 直接在该二维库上重建, 并与原三维信息进行比较。

2) 库外测试。即选取已规范化的100个三维人脸数据作为训练集, 直接对实际照片进行重建。实际照片来自CAS-PEAL二维人脸数据库。

3.1 库内测试

实验共选取人面部47个特征点, 对笔者提出的三维人脸稀疏分步重建与基于稀疏形变模型的三维重建分别进行实验, 并与现有相关三维重建方法做比较。

对于三维人脸数据库内样本, 由于已知其真实三维信息, 故实验采用平均欧氏距离[6]作为重建精度评价标准, 将重建得到的三维数据与原始数据直接比较。重建精度(重建误差)计算如下

(12)

其中So,Sr分别是两个形状的曲面,V是曲面上的顶点集合,Vo,Vr分别是So,Sr上的顶点。eeuc越小, 则代表重建结果与真实结果越吻合, 即重建精度越高, 重建误差越小。

实验第1步共选取人面部12个关键特征点以及3对位于边缘轮廓上的点, 初步确定待重建人脸的脸型与关键区域的大体位置； 第2步采用面部其余特征点, 以确定关键区域的具体细节信息。对两步重建中的扰动因子分别取值, 计算其最终重建误差。经过多次试验,η1=0.85,η2=3.4时, 平均重建误差最小。故对于测试集所有样本, 均取η1=0.85,η2=3.4。选用稀疏形变模型(SRSD: Surface Reconstruction from Sparse Data)重建算法作比较, 部分实验结果如图4所示。

a 二维投影人脸 b 第1步结果 c 第2步结果 d 真实三维信息 e SRSD重建结果

由图4可看出, 分步形变的结果更加接近真实三维人脸, 且在面部细节上与稀疏形变模型相比表现得更加细致。而稀疏形变模型的结果普遍与第1次形变的结果较为相似, 这是由于稀疏形变模型所选用的部分特征点对整个重建结果的影响较小, 仅采用人脸部分关键特征点即可形变得到初步的三维人脸重建模型。

表1 相关算法的重建误差比较

笔者选择与笔者相关的基于稀疏形变模型的三维人脸重建算法和文献[17]提出的SDM(Sparse Deforming Model)算法作比较, 分别计算其欧氏距离, 最终结果为测试集上30个样本的误差均值。精度对比如表1所示。其中SRSD与SDM的保留主成分数目为69, 其余参数设置均参照文献[5]和文献[15]。

结合图3与重建误差实验比较可以得出, 笔者算法与SRSD相比, 精度提高了约10%, 与SDM相比, 精度提高了1.85 mm。

实验同时比较了不同算法的速度, 将常见三维人脸重建算法所需时间与笔者所述算法进行对比。其中SRSD和笔者算法均用Matlab 2012a实现, 包含用于主成分分析的时间, 其余算法时间分别引自文献[2]、 文献[6]、 文献[12]和文献[8]。实验结果如表2所示。

表2 相关算法的重建速度比较

从相关算法的速度比较可看出, 笔者提出的分步三维重建算法速度与传统的稀疏形变模相比, 尽管在第1轮重建结果的基础上引入第2轮重建, 但Matlab实现的算法速度与之相当(稍慢0.02 s)。与经典的形变模型算法相比, 笔者提出的算法速度具有很大的提高。综合重建精度和重建速度比较, 笔者提出的基于分步重建的三维人脸稀疏重建算法具有一定的优势。

3.2 库外测试

该实验采用CAS-PEAL二维人脸数据库中POSE子集中随机抽取的个人照片作为测试库。对于库中的图片, 实验对正脸照片进行重建, 重建的结果以不同角度的侧面与数据库中对应角度的照片进行比较, 部分实验结果如图5所示。

a 输入2D图像 b 三维重建结果 c 输入图像侧面 d 重建结果侧面 e 输入图像侧面 f 重建结果侧面

对真实照片的重建结果可看出, 笔者提出的方法能一定程度上还原二维人脸的三维信息, 相比于传统的重建方法, 笔者方法能在重建精度上得到一定的提高。但由于训练样本库较小, 且方法的根本是由少量点控制整体形变等原因, 三维重建的结果仍然在细节上存在一定误差。

4 结 语

笔者在传统稀疏形变模型三维人脸重建方法的基础上, 提出了一种基于分步重建的稀疏三维重建方法, 并在BJUT-3D Face Database和CAS-PEAL数据库中做了测试。实验表明, 该算法能在重建速度较快的基础上, 与经典算法相比提高一定的重建精度。由于采用两步重建三维人脸, 每步的特征点数量的选择以及参数设置都会影响最终结果和重建精度, 因此, 相关参数的选择和优化将是进一步研究的重点。

参考文献：

[1]徐琳, 袁保宗, 高文. 真实感人脸建模研究的进展与展望 [J]. 软件学报, 2003, 14(4): 804-810.

XU Lin, YUAN Bao-zong, GAO Wen. Development and Prospect on Realistic Facial Modeling [J]. Journal of Software, 2003, 14(4): 804-810.

[2]BLANZ V, VETTER T. A Morphable Model for the Synthesis of 3D Faces [C]∥ Computer Graphics Proceedings, SIGGRAPH’99. New York, USA: [s.n.], 1999: 187-194.

[3]BLANZ V, VETTER T. Face Recognition Based on Fitting a 3D Morphable Model [J]. IEEE Trans Pattern Analysis and Machine Intelligence, 2003, 25(9): 1063-1074.

[4]PATEL A, SMITH W A P. 3D Morphable Face Models Revisited [C]∥Proc IEEE Conf Computer Vision and Pattern Recognition. Miami, FL, USA: IEEE, 2009: 1327-1334.

[5]王成章, 尹宝才, 孙艳丰, 等. 改进的基于形变模型的三维人脸建模方法 [J]. 自动化学报, 2007, 33(3): 232-239.

WANG Cheng-zhang, YIN Bao-cai, SUN Yan-feng, et al. An Improved 3D Face Modeling Method Based on Morphable Model [J]. Acta Automatica Sinica, 2007, 33(3): 232-239.

[6]BLANZ V, VETTER T. Reconstructing the Complete 3D Shape of Faces from Partial Information [J]. It-Information Technology, 2002, 44(6): 295-302.

[7]胡阳明, 周大可, 鹿乐, 等. 基于形变模型的三维人脸快速重建改进算法 [J]. 吉林大学学报: 信息科学版, 2012, 30(6): 605-609.

HU Yang-ming, ZHOU Da-ke, LU Le, et al. Improved 3D Fast Face Reconstruction Algorithm Based on Morphable Model [J]. Journal of Jilin University: Information Science Edition, 2012, 30(6): 605-609.

[8]胡永利. 真实感三维人脸建模及应用研究 [D]. 北京: 北京工业大学计算机科学与技术学院, 2004.

HU Yong-li. Realistic 3D Face Modeling and Its Application [D]. Beijing: School of Computer Science and Technology, Beijing University of Technology, 2004.

[9]PATEL A, SMITH W A P. Driving 3D Morphable Models Using Shading Cues [J]. Pattern Recognition, 2012, 45(5): 1993-2004.

[10]尹宝才, 何晏晏, 孙艳丰, 等. 三维人脸的非均匀重采样对齐算法 [J]. 北京工业大学学报, 2007, 33(2): 213-218.

YIN Bao-cai, HE Yan-yan, SUN Yan-feng, et al. Nonuniform Resampling Based on Method for Pixel-Wise Correspondence between 3D Faces [J]. Journal of Beijing University of Technology, 2007, 33(2): 213-218.

[11]LIAO H B, CHEN Q H, ZHOU Q J, et al. Rapid 3D Face Reconstruction by Fusion of SFS and Local Morphable Model [J]. Journal of Visual Communication and Image Representation, 2012, 23(6): 924-931.

[12]KEMELMACHER-SHLIZERMAN I, BASRI R. 3D Face Reconstruction from a Single Image Using a Single Reference Face Shape [J]. IEEE Trans Pattern Analysis and Machine Intelligence, 2011, 33(2): 394-405.

[13]KEMELMACHER-SHLIZERMAN I, BASRI R. Molding Face Shapes by Example [C]∥Proc European Conference on Computer Vision. Graz, Austn: [s.n.], 2006: 277-288.

[14]龚勋, 王国胤. 基于特征点的三维人脸形变模型 [J]. 软件学报, 2009, 20(3): 724-733.

GONG Xun, WANG Guo-yin. 3D Face Deformable Model Based on Feature Points [J]. Journal of Software, 2009, 20(3): 724-733.

[15]龚勋. 基于单张二维图片的三维人脸建模 [D]. 重庆： 西南交通大学信息科学与技术学院, 2008.

GONG Xun. 3D Face Modeling Based on a 2D Image [D]. Chongqing: School of Information Science and Technology, Southwest Jiaotong University, 2008.

[16]徐成华, 王蕴红, 谭铁牛. 三维人脸建模与应用 [J]. 中国图像图形学报, 2004, 9(8): 893-903.

XU Cheng-hua, WANG Yun-hong, TAN Tie-niu. Overview of Research on 3D Face Modeling [J]. Journal of Image and Graphics, 2004, 9(8): 893-903.

[17]柴秀娟, 山世光, 卿来云, 等. 基于3D人脸重建的光照、 姿态不变人脸识别 [J]. 软件学报, 2006, 17(3): 525-534.

CHAI Xiu-juan, SHAN Shi-guang, QING Lai-yun, et al. Pose and Illumination Invariant Face Recognition Based on 3D Face Reconstruction [J]. Journal of Software, 2006, 17(3): 525-534.