基于经验方法的涡轮损失计算研究

白创军，刘超，徐伟祖，钟易成

（1.中航工业南方航空工业（集团）有限公司，湖南株洲412002;2.南京航空航天大学动力与能源学院，江苏南京210016;3.南京普国科技有限公司，江苏南京 210016）

0 引言

在涡轮设计中，涡轮损失的准确预测对于涡轮性能评估，提高涡轮效率起到关键的作用。涡轮损失的预测方式主要有试验方法，CFD方法和经验方法。本文对涡轮预测所使用方法为经验方法，该方法的优点比较明显，计算简便，快捷，在涡轮初步设计中被广泛运用。经验方法主要依赖于各种损失模型，损失模型的建立最早从20世纪50年代就开始进行，经历了50多年的发展已经日益成熟。模型的发展分为两个时期［1］:第一个时期的模型主要是根据试验数据为基础，归纳而成的计算模型;第二个时期的模型注重于研究引起损失的物理本质，通过研究边界层特征和损失的关系来了解损失的机理，因此并不适用于工程应用。损失计算模型按计算范围分可分为两类，一类只能计算设计状态下的损失，包括半经验模型、Traupel、Balje＆Binsley、Stewart等模型，一类能够预测非设计状态下的损失，包括 AMDC、KO、Moustapha模型和 Craig＆Cox模型;如果按计算损失类型分又可分为压力损失模型和能量损失模型，但压力损失和能量损失可以互相转换。

本文用到的损失模型主要为第一代模型，通过C++对各种经验模型算法进行编程，开发了一套预测涡轮损失的软件，软件中包含10种损失模型，可以通过输入涡轮几何参数和部分进出口气动参数来计算涡轮的各项损失。由于篇幅有限这里主要介绍3个计算压力损失的模型AMDC模型、KO模型、Moustapha模型和一个计算能量损失的半经验模型。

1 损失计算模型介绍

1.1 AMDC 模型

Ainley＆Mathieson［2］在 1951 年给出了一种预测涡轮损失的模型，并在之后多年的涡轮性能分析中得到应用，二次流损失计算方法又经 J.Dunham＆P.M.Came（1970）［3］改进。它的总损失由叶型损失、二次流损失以及叶尖间隙损失组成，并受尾缘系数XTe的影响。

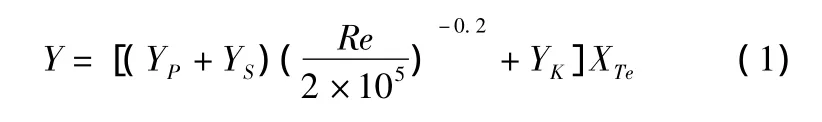
设计点下叶型损失公式为:

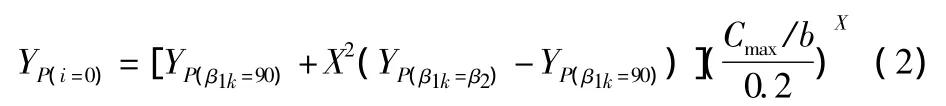
式中:YP（β1k=90°）为进口几何角 β1k=90°下的小转角叶栅的叶型损失系数;YP（β1k=β2）为进口几何角 β1k= β2下的大转角叶栅的叶型损失系数，可通过文献［1］Fig.4得到。非设计点下叶型损失公式为:

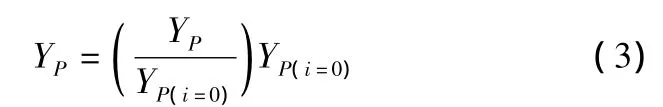
YP/YP（i=0）为攻角因子，通过文献［1］中Fig.6和Fig.7得到。二次流损失取决于叶片载荷、叶型和端壁附面层:

叶尖间隙损失系数YK与叶片载荷、叶尖间隙的大小和叶尖处的结构形式有关:

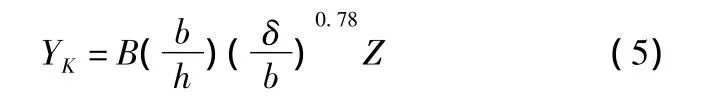
对于不带叶冠B=0.47，一般带叶冠B=0.37;Z代表叶片载荷，文献［2］给出了它的计算方法。

1.2 其它损失模型

Kacker＆Okapuu（1982）［4］模型在计算叶型损失的部分主要是基于AMDC模型给出的。该模型重新构造了损失体系，考虑了气流压缩性和激波损失并引入到叶型损失和二次流损失的计算中。总损失为:

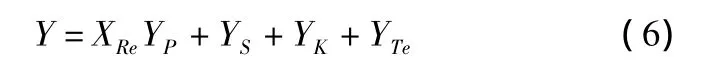
叶型损失的计算公式如下:

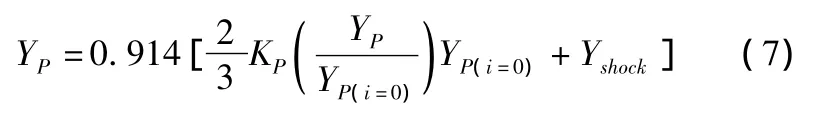
二次流损失的计算公式如下:

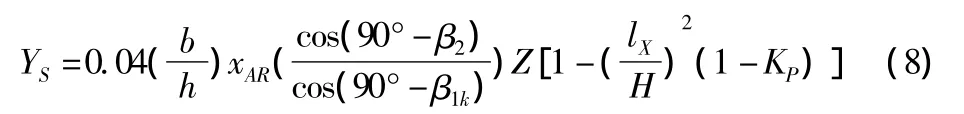
1990 年，Moustapha［5］等人给出了预测非设计点的叶型损失和二次流损失的损失模型。Moustapha给出的攻角损失是叶片前缘直径、栅距、展弦比和槽道收敛度的函数。引入一个因子x':

当0＜x'＜800时:

ΔζP=0.778 ×10－5x'+0.56 × 10－7x'2+0.4 ×10－10x'3+2.054 ×10－19x'6

当－800＜x'＜0时:

ΔζP= －5.173 4 ×10－6x'+7.690 2 ×10－9x'2

通过研究，Moustapha等注意到二次流损失也会随攻角的变化而变化，因此在文献中提出了非设计点二次流损失的概念。引入一个因子x″:

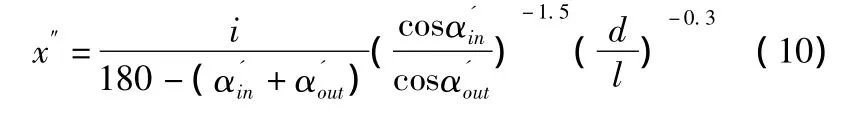
当0＜x″＜0.3时:

当 －0.4＜x″＜0时:

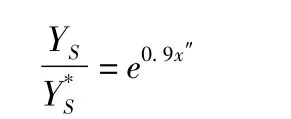
半经验模型［6］是通过试验结果总结归纳的一种损失预估方法，半经验公式包含叶型损失和二次流损失的计算方法，具有准确性高和简单的特点，可以满足工程设计的需要。它的总损失为:

其中叶型损失的计算公式如下:

二次流损失计算公式如下:

当叶片平均展弦比≥2时，

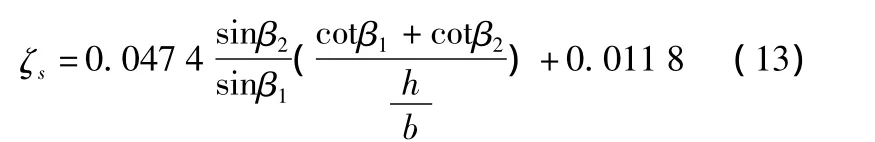
当叶片平均展弦比＜2时，

叶尖损失是采用Hong Yong S［7-8］于1966年的试验结果进行计算，对于小的叶尖间隙试验结果得到的叶尖漏泄损失值是比较满意的。

2 涡轮参数和网格计算

所选用的涡轮算例为自主设计的轴流式动力涡轮，为双级涡轮的第二级。算例中选取了叶片中截面的参数作为计算的平均参数。图1描述了涡轮级静叶和动叶的叶型形状和计算网格。

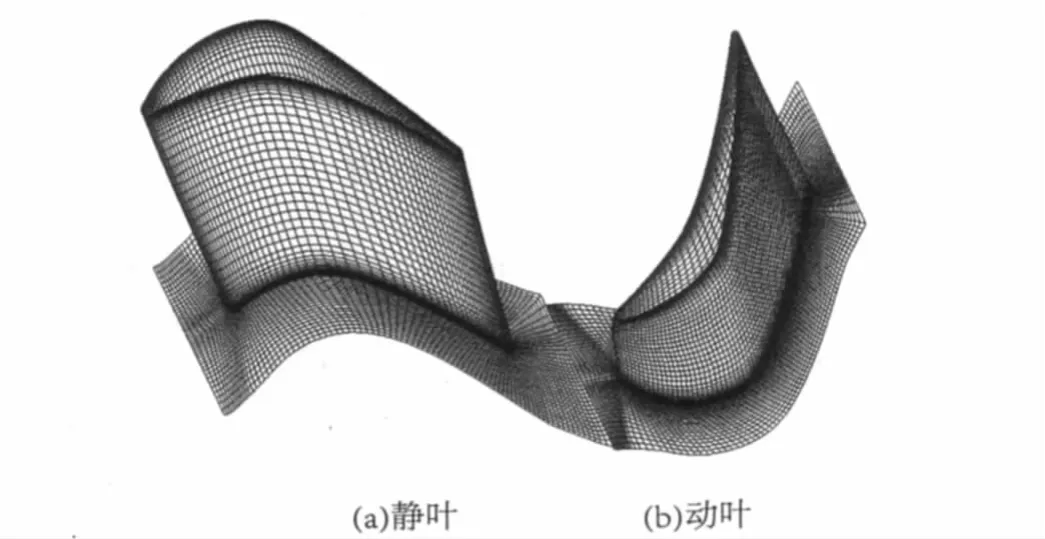
图1 涡轮叶型和计算网格

表1分别给出了涡轮的几何参数和气动参数，其中动叶的气动参数都为相对值。

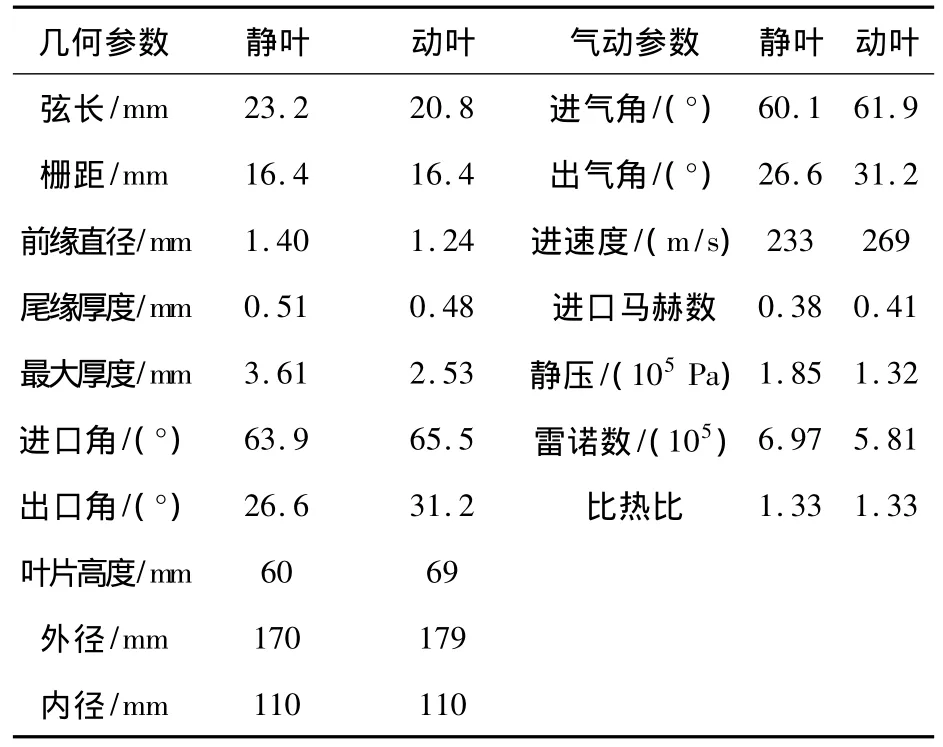
表1 算例涡轮几何参数和气动参数

为了验证这四种模型计算结果的可靠性，对算例涡轮进行CFD计算。采用商业软件TurboGrid软件划分结构化六面体网格，网格总量为35万（图1）。叶片前缘劈分成H型结构，尾缘为J型结构，叶片表面采用O型结构［9］（图2），径向网格单元数为16，近壁面最小网格单元高度为0.012 mm。

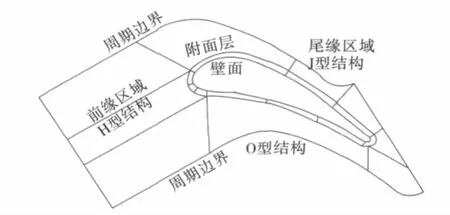
图2 S1流面几何分块

CFD预测的压力损失大小可以通过压力损失的定义来计算，对于静子:

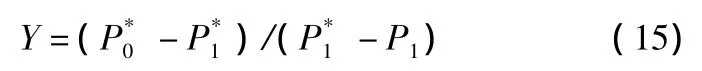
对于转子:

其中，和分别为静子的进出口总压，P1为静子的出口静压和为转子相对进出口总压，P2为转子出口静压。

3 软件计算与结果分析

本文通过已有软件和CFD分别对涡轮算例设计点下静子叶片和转子叶片进行了计算，并计算了涡轮级的效率。同时对非设计点攻角变化下的静叶损失进行了统计，通过和CFD的计算结果进行对比，分析了各个模型的优缺点。由于尾缘损失值比较小，且受攻角影响比较小，故图表中没有给出它的值。

3.1 设计点下各模型计算结果

图3和图4分别给出了涡轮算例静叶和动叶设计点下的各项损失和总损失的计算结果。半经验算法计算结果为能量损失，可以通过下式转换为压力损失。

其中Mout为出口马赫数，γ为比热比，ζ为能量损失系数。

涡轮级效率可以通过静叶损失和动叶损失来计算［10］，公式如下:

其中LCT代表涡轮级燃气所做的功，L'r代表涡轮个别组件不可逆损失功:

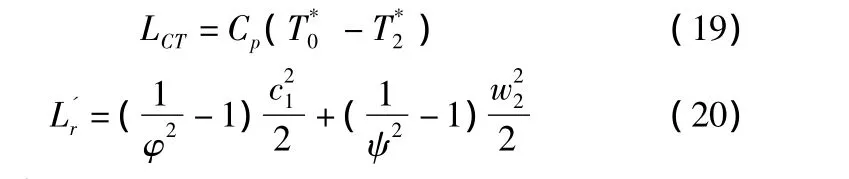
φ2和ψ2代表静子和转子的速度损失系数，它们可以通过公式与能量损失系数及压力损失系数相互转换。各模型涡轮级的效率如图5所示。

图5 涡轮级总效率大小

通过以上的计算结果可以看出:在静子叶片中，AMDC模型的总损失比KO模型要大，尤其是叶型损失系数，计算结果相差将近一倍，主要原因是KO模型在AMDC模型的基础上引入了马赫数修正因子，当静子出口马赫数大于0.2时，叶型损失会变小。而在计算转子叶片中，AMDC模型的叶型损失却＜KO模型的计算结果，这是因为转子叶片下KO模型产生了激波损失，KO认为当叶片进口轮毂处的马赫数＞0.4时，就产生了激波损失，它的大小受进出口压力、进出口马赫数和涡轮内外径比等因素影响。Moustapha模型和KO模型在0攻角下的计算结果是相同的，它是在KO模型基础下对攻角变化时损失的修正。

总效率计算中，CFD的结果比以上几种压力损失模型都要小，其中差别主要体现在转子叶片上，这和CFD在转子叶片中进出口相对总压的计算误差有一定关系。半经验算法的总效率比CFD的结果更小，这是因为它在静子处的损失过大，尤其是叶型损失，它只考虑到了进出口气流角对叶型损失的影响，相比以上几种模型不够准确。

3.2 非设计点下各模型计算结果

软件中选取了3种压力损失模型来计算非设计状态下攻角影响下的损失。在原先的设计参数下通过改变进口气流角大小来获得不同的攻角对涡轮的静子进行计算，攻角变化范围为 －50°～30°。

AMDC模型转子损失的预测结果在图6（a）所示，通过计算结果可以看出，叶型损失的最小值是在攻角为零处，随着攻角的增大或减小，叶型损失也会逐步增大。二次流损失随着攻角的增大而增大，这是由于随着进口气流角的增大，气流进出口角的变化也增大，这样在高转折角下叶片升力系数增加，最终导致了二次流损失的增加。总损失是由叶型损失，二次流损失和尾缘损失组成，总损失的最小处在攻角约等于－10°处。KO模型静子损失的预测结果在图6（b）所示，叶型损失的最小值是在攻角为零处，当攻角变化时，叶型损失也会增加。这与AMDC模型预测的变化趋势相类似，不同的是KO的叶型损失要小于AMDC的损失。二次流损失是随着攻角的增大而变大。总损失是由叶型损失，二次流损失和尾缘损失组成，总损失的最小处在攻角约等于－20°处。

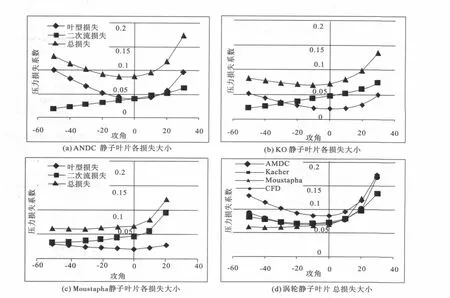
图6 各模型计算的静子叶片压力损失系数

Moustapha模型静子损失的预测结果在图6（c）所示，叶型损失的最小值也是在攻角为零处，但是相比以上两种模型变化并不明显，当攻角增大或减小到一定值时，叶型损失才会有明显的增加。Moustapha模型考虑了攻角变化对二次流损失的影响分析，给出了一个乘积因子，认为二次流非设计状态下的损失为设计点损失乘于乘积因子，当攻角为正时乘积因子大于1且不断增加;而当攻角为负时乘积因子小于1且不断减小。所以Moustapha模型的二次流损失随攻角变化相比之下比较明显。总损失在－40°处迎来最小值。

本文同时也给出了非设计点状态下不同攻角下的的CFD计算结果，攻角的获取也是通过改变进口气流角完成的，通过－50°～30°间选取9个点进行计算。为了直观的了解不同攻角下叶型周围的流场变化，本文给出了各个攻角下静压的分布和速度流线图（图7）。

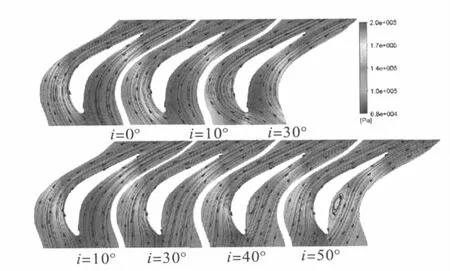
图7 叶型周围静压分布和速度流线图

从图中可以看出，攻角在－30°到10°变化时，叶片附近流场比较均匀。当攻角＞20°时，叶片吸力面附面层发生明显的分离并产生了通道涡，且涡的大小随攻角的增大而增大。而当攻角＜－40°时，叶片压力面也开始产生了通道涡。

三种压力模型的计算结果和CFD的计算结果在图6（d）中给出，可以看出:在负攻角下，KO模型的预测结果最为准确，AMDC的预测结果偏大而Moustapha的预测过于保守。当攻角为正且＜10°时，几种模型的预测结果都较为准确;当正攻角增加到20°时，Moustapha的损失变化突然变得急剧并加速上升;当攻角进一步增加时，叶片吸力面附面层分离加剧，于是各损失模型预测的结果都不够准确，KO的损失变化过于平缓，虽然AMDC的变化曲线和CFD相似，可预测的值要明显偏大一些。

Moustapha模型的可靠区间在攻角－20°～10°;KO模型的可靠区间在－50°～20°;而AMDC模型预测结果相比CFD结果偏大，但当攻角在20°～30°，结果和CFD最为接近。

4 结论

根据上述几种损失模型在设计点和非设计点的计算以及和CFD的结果对比，可以得出以下结论:

1）由于在基本原理和基本假设等方面的不同，不同损失模型的预测结果有一定的差异。对于AMDC、KO和Moustapha这三种模型，静叶中的差别主要体现在叶型损失上，动叶中的差别主要体现在二次流损失上。

2）在本算例中，各模型的总效率差别不大，不超过1.5%。其中CFD在设计点的总效率要小于三个压力损失模型，区别主要来自于在转子叶片上;KO和Moustapha模型的效率相比AMDC和CFD更为接近;而半经验算法的总效率比CFD的结果更小。

3）通过对静子叶片的计算，本文中研究的三种非设计状态下的涡轮损失预测模型能很好地反映出涡轮损失随攻角变化的趋势:正攻角时损失比同样负攻角时的损失来得大;零攻角时的损失并不是最小，最小损失通常在－10°左右出现。

［1］华鑫，乔渭阳.基于流线曲率法的航空轴流涡轮损失模型研究［J］.机械设计与制造，2005（12）.

［2］Ainley D G，Mathieson G C R.A Method of Performance Estimation for Axial-Flow Turbines［R］.British Aeronautical Research Council，R＆M 2974，1951.

［3］Dunham J.A review of Cascade Data on Secondary losses in Turbines［R］.Journal Mechanical Engineering Science，Vol.12，No.1，1970.

［4］Kacker S C，Okapuu U.A mean Line Prediction Method for Axial Flow turbine Efficiency［R］.ASME，81-GT-58，1982.

［5］Moustapha S H，Kacker S C，Tremblay B.An Improved Incidence Losses Prediction Method for Turbine Airfoils［R］.ASME，89-GT-284，1990.

［6］黄庆南.航空发动机设计手册.第10册:涡轮［M］.北京:航空工业出版社，2001.

［7］A.J.格拉兹曼.涡轮设计与应用［M］（第二版）.北京:国防工业出版社，1982.

［8］Hong Yong S，Groh F G.Axial Turbine Loss Analysis and Efficiency Prediction Method［R］.Rep.D4-3220，Boeing Co，Mar.11，1966.

［9］ANSYS Turbo Grid User’s Guide:ANSYS Turbo Grid Workflow，Topology［EB/OL］.

［10］С.З.柯别列夫，Н.Д.吉洪诺夫.航空发动机涡轮计算（气动计算及叶片造型）［M］.北京:国防工业出版社，1978.