基于FPGA的SVPWM算法在变频调速中的实现

褚福领，李志刚，高子龙

（南京理工大学机械工程学院，江苏南京 210094）

0 引言

随着电气传动系统对其控制性能的要求不断提高，人们对PWM控制技术展开了深入的研究。从最初追求电压正弦波到电流正弦波，再到磁通正弦，PWM控制技术进行了不断的创新和完善。在此，对空间矢量PWM（SVPWM）进行了分析。SVPWM是一种更优化的PWM技术，与传统SPWM技术相比，具有控制算法简单，数字化实现方便，电压利用率高，谐波成分少等优点，因此有取代SPWM的趋势［1］。为了满足SVPWM算法的高性能，常常需要将控制周期缩短到几百微秒，甚至几十微秒之内。然而，普通单片机已无法满足要求。FPGA以其高性能的运行速度，理所当然地被用于SVPWM及交流调速控制场合。SVPWM物理概念清晰，算法简单，易于使用FPGA器件采用数字的方式实现。本文介绍了SVPWM的基本原理、算法以及基于FPGA的实现，并给出了仿真波形的实验结果，有一定的工程实现价值。

1 空间矢量脉宽调制（SVPWM）原理

图1 电压型逆变器主电路

图1为电压型逆变器结构简图，每一个桥臂有上下两个开关器件，同一桥臂的两个开关器件不能同时导通。若规定每个桥臂上桥臂导通且下桥臂关断为“1”，而下桥臂导通且上桥臂关断为“0”，三组开关共有8种可能的开关组合，如表1所示。

表1 电压型逆变器8种基本开关状态表

根据式（1）、（2）可知逆变器开关状态和电压之间关系，如表2所示。

表2 逆变器开关状态和三相电动机瞬态电压关系

三相定子电压通过Clarke变换，可得静止坐标系下的α 轴、β 轴电压分量［2］:

由于VCN=-（VAN+VBN），将上式转换成矩阵形式:

由式（3）、（4）可知逆变器开关状态和静止坐标下（α，β）电压之间关系，如表3所示。

表3 开关状态、相电压（α，β坐标系）、空间矢量关系

2 控制算法

由前一节介绍可知SVPWM技术主要是通过调节开关状态得到相应的基本空间矢量，迫使接近给定定子参考电压矢量UOUT。要实现SVPWM必须先判断参考电压矢量UOUT所在的扇区;再计算开关电压矢量的作用时间;最后确定开关顺序。

2.1 判断空间矢量UOUT所处扇区

输出电压矢量UOUT可以用相邻电压矢量在（α，β）坐标下的分量Ualfa和表示Ubeta，以第一象限为例，其矢量表示如图2:

图2 参考电压投影图

式中:ΣVsβ代表基本电压矢量U0和相邻基本电压矢量U60在β轴电压分量之和，ΣVsα代表基本电压矢量U0和相邻基本电压矢量U60在α轴电压分量之和。可以通过改进的Clarke逆变换将静止坐标系下的α轴、β轴电压分量变换为三相平衡分量Vref1，Vref2，Vref3。

根据下面的比较分析，可以决定空间矢量所处的扇区:

定义A、B、C三个变量。如果Vref1＞0则A=1，否则A=0;如果Vref2＞0则B=1，则B=0;如果Vref3＞0则C=1，否则C=0，则空间矢量所在扇区可表示为N=A+2B+4C。

根据扇区与N值的对应关系表确定扇区号，如表4所示。

表4 N值与扇区对应关系

2.2 计算非零电压矢量作用时间

从图2电压矢量图可以知道，输出电压矢量Uout处于U0和U60所夹的扇区，因此，输出电压矢量Uout可以用电压矢量U0和电压矢量U60表示。所以可以得到如下等式:

式中:T1，T3分别代表电压空间矢量U0和U60导通时间，T代表Uout的作用时间，T0代表零矢量导通时间，导通时间可以用式（8）表示:

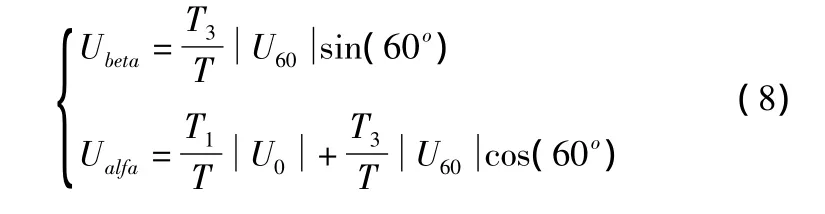
那么对于第一象限的空间矢量的导通时间可表示为:T1=-Z，T3=X。同理，当Uout在其他扇区时，相应的导通时间T1、T2也可用X、Y、Z表示，它们的对应关系如表5所示。

表5 T1、T2与X、Y、Z之间的对应关系

对作用时间还应进行饱和判断［3］，当T1+T2＞T时，经过式（11）计算饱和判断后的T1、T2:

2.3 计算各相上桥臂开关管导通时刻

式中Ts为PWM的周期，电压矢量切换点Ta，Tb，Tc与扇区的对应关系如表6所示。

表6 电压矢量切换点与扇区对应关系间的对应关系

3 伺服驱动控制器硬件设计

伺服驱动控制器总体电路原理图如图3所示:

图3 伺服驱动控制器总体电路原理图

在FPGA控制器电路中，FPGA芯片选择CycloneⅡ系列中的EP2C8Q208C8N型号。并配置相应的最小系统功能必需的核心器件，如表7所示:

表7 最小系统配置核心器件表

功率逆变器的IGBT的栅极驱动控制端工作在-5 V～15 V区间，故需要设计功率逆变器驱动控制电路来实现FPGA控制器和功率逆变器之间衔接。

4 软件设计与实验结果

将前述的各个模块加上分频模块连接起来构建出电压空间矢量脉宽调制总体设计，在FPGA中实现的总体构成如图4所示:

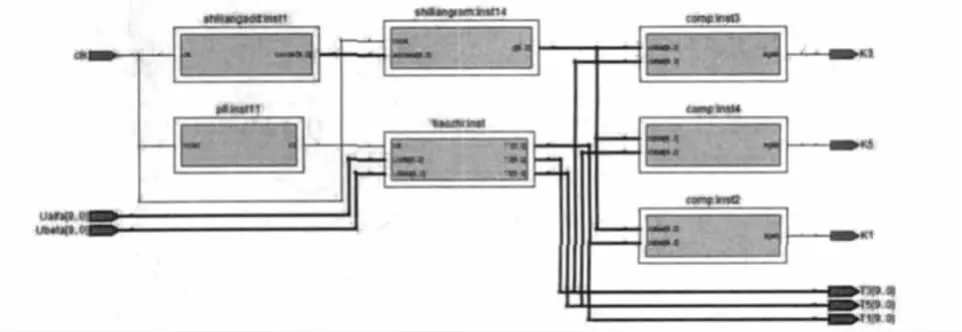
图4 电压空间矢量脉宽调制FPGA实现的总体构成图

对于电压空间矢量脉宽调制变频控制，在数字实现时，依据标准IGBT开关的动作频率为10 kHz，对每个三角波周期采用采样频率为20 MHz的数字采样构建三角波［5］。三角载波模块FPGA实现原理如图5所示:

图5 三角载波模块FPGA实现原理图

在FPGA中实现当前电压矢量Uout处于不同扇区时，各相上桥臂开关管S1，S3，S5的脉冲驱动控制信号重构的功能仿真如图6所示:

图6 各相上桥臂开关管驱动控制信号重构FPGA实现的功能仿真图

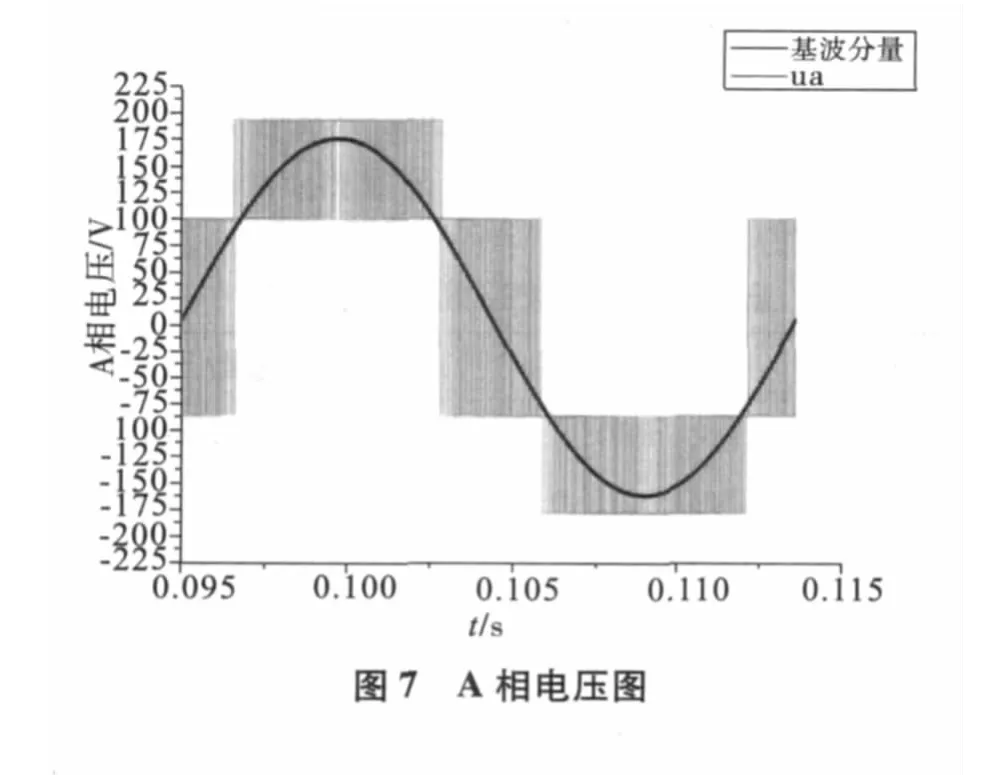
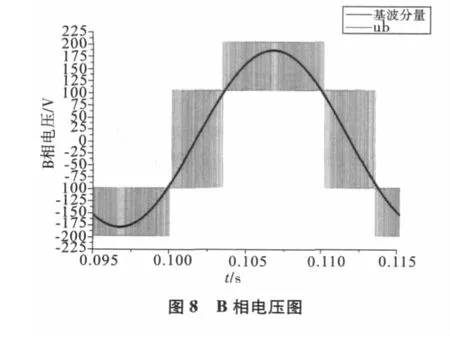
将驱动脉冲控制信号作用的功率逆变驱动控制电路，进而驱动功率逆变器，在输入整流直流电压为300 V时，输出相应的相电压，相电流如图7—图10所示:

5 结论

从图7—图10可以得出，各相电压中的基波分量与期望输出的三相正弦相电压频率、相位相一致;相电压和相电流存在谐波畸变，对上述得到A相输出电压进行快速傅里叶变换的得到其谐波分析如图11所示:

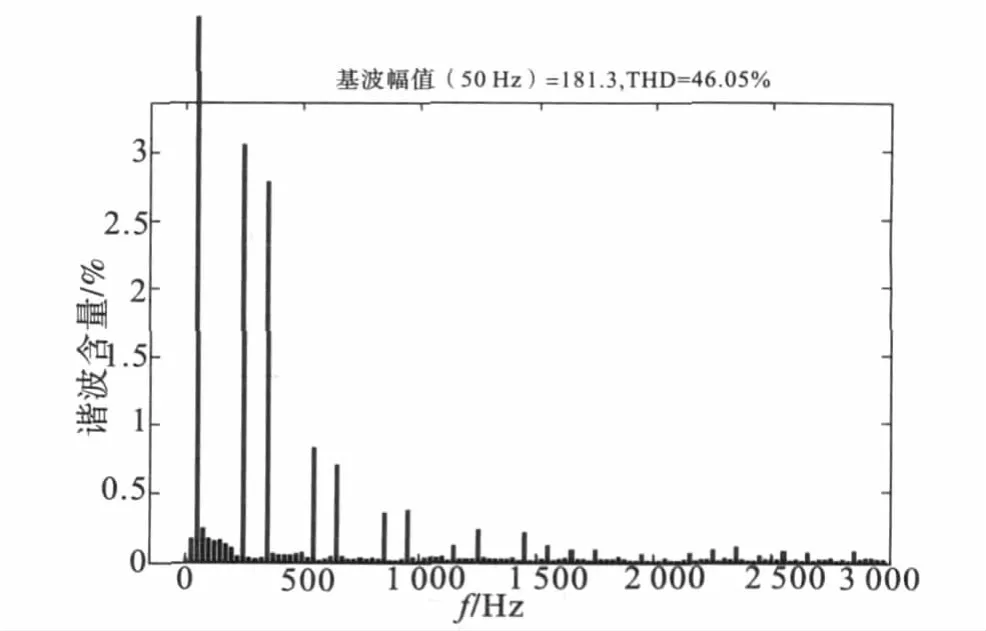
图11 电压空间矢量脉宽调制输出A相电压谐波分析图

在最高频率为3 000 Hz时，A相输出的相电压的基波幅值为181.3 V，THD为46.05%，A相输出的相电压流的THD为4.93%。电压空间矢量脉宽调制的线电压的基波幅值为300 V，与理论的分析相一致，直流电压利用率为100%。

故由以上分析可得，电压空间矢量脉宽调制具有很高的利用率，作为接收对数字PI控制器的电压信号的变频控制方式，可以使得PMSM具备更高的控制精度和更好的能源利用率，SVPWM算法不仅易于数字化实现，便于实时控制，而且直流电压利用率高，控制性能好。

［1］寇保泉，程树康 .交流伺服电机及其控制［M］.北京:机械工业出版社，2008:45-50.

［2］郭庆鼎，孙宜标，王丽梅.现代永磁电动机交流伺服系统［M］.北京:中国电力出版社，2006:63-73.

［3］何杰，王家军.基于SVPWM的永磁同步电机系统建模与仿真［J］.机电工程，2009，26（7）:77-88.

［4］祁超，王庆章，赵耀，等.基于F P G A的三相SV P W M调制算法的实现［J］.南开大学学报（自然科学版），2011，4（44）:28-29.

［5］郑飞，费树岷，周杏鹏，等.基于DSP和FPGA的SVPWM算法及其在变频调速中的应用［J］.电力自动化设备，2010，11（30）:61-63.