三体量子系统态的可分离性判据
2013-10-12李嫦娥陶元红丁巍巍
李嫦娥,陶元红,丁巍巍
(延边大学理学院 数学系,吉林 延吉 133002)
0 引言
量子纠缠现象被视为一种重要的物理资源.量子纠缠广泛应用于量子处理,如量子计算、量子编码、量子隐形传态等[1].关于纠缠态的数学结构和物理特性还没有被完全了解.近年来,关于判断纠缠态可分判据见文献[2-11].笔者给出三体量子系统密度矩阵所在线性空间的Hamel基,以及三体量子系统密度矩阵的表示形式,并提出三体量子系统密度矩阵可分离的一个判据.
1 预备知识
一个独立的R维Hilbert空间上的厄米特算子总可以由单位算子I和特殊酉群SU(R)的生成元表示[2].SU(R)的生成元可以用R×R阵初等矩阵构造,其中,为k行j列为1,其余元素为0的矩阵[2].SU(R)群的一组典型生成元共有R2-1个,它们是迹为0的R×R阶矩阵,不妨设为.这R2-1个典型生成元与R×R 阶单位算子I一起构成线性空间MR(C)的一个完备的厄米特算子基
引理1.1[9]设SU(R)群的R2-1个独立生成元为{λi|i=1,2,…,R2-1},则
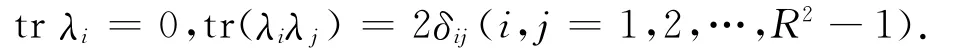
引理1.2[7]设单粒子量子态空间维数为R,ρ可以表示为,其中均为实数,且满足
由于任意量子系统的密度算子都是半正定的厄米特算子,所以密度算子也可以由特殊酉群SU(R)的生成元和单位算子表示.
定义1.1 若三体量子系统A,B,C的量子态用密度矩阵ρABC描述,且,其中分别为系统A,B,C的密度矩阵,则称可分;否则,称为纠缠.
设T为任意矩阵,TT表示矩阵的T转置,T+表示矩阵T的转置共轭,取T的Frobenius范数为
2 主要结论
首先研究三体量子系统密度矩阵所在线性空间的Hamel基,其次讨论三体量子系统密度矩阵的表示形式,最后给出三体量子系统密度矩阵可分离的一个必要条件.
定理2.1 设三体量子系统A,B,C的空间维数分别为R1,R2,R3,则由矩阵组成的集合S是线性无关的,并构成线性空间的一个 Hamel基.
证明:为了证明集合S是线性无关的,先设

故(1)式可变为

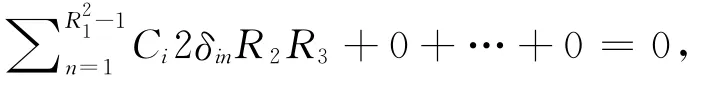
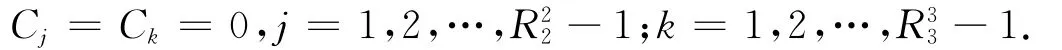
因此有

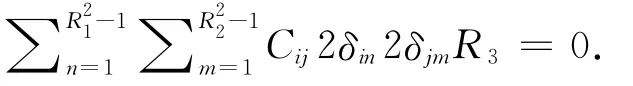

因此得


由上述定理容易得到密度矩阵的表示形式.

其中,实系数为
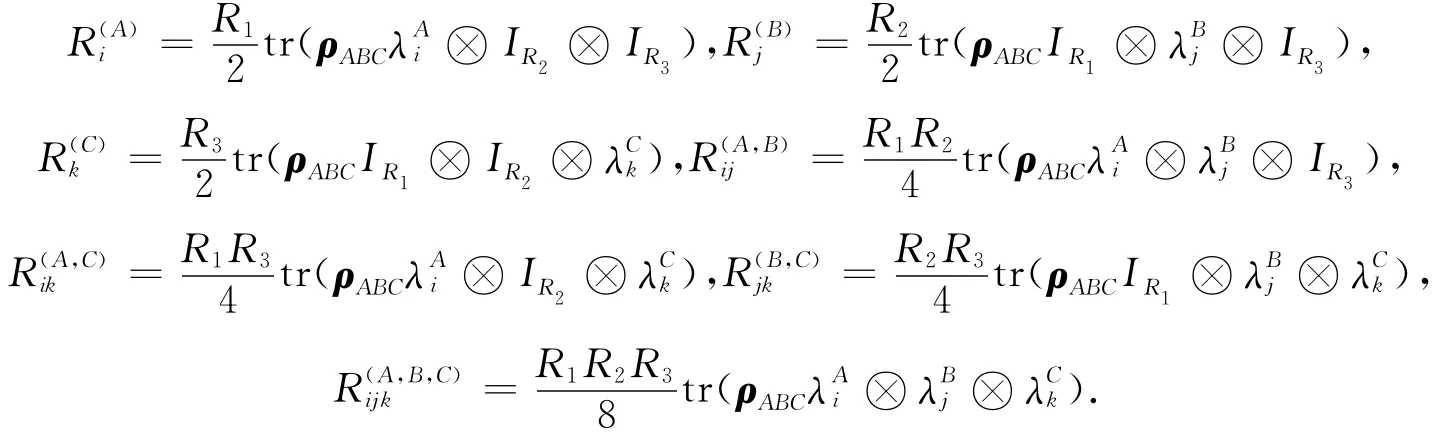
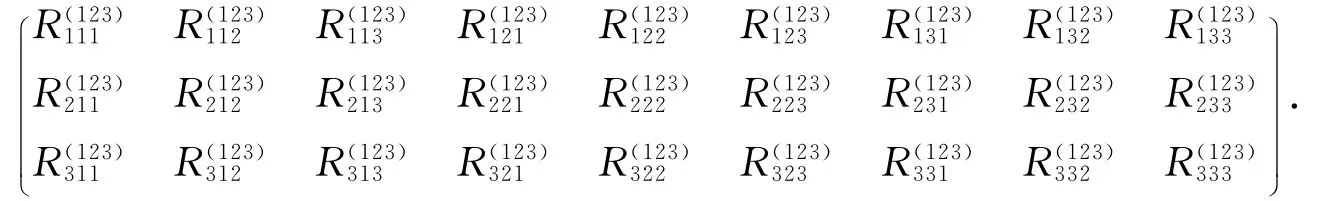
给出三体量子系统密度矩阵的一个可分离判据.
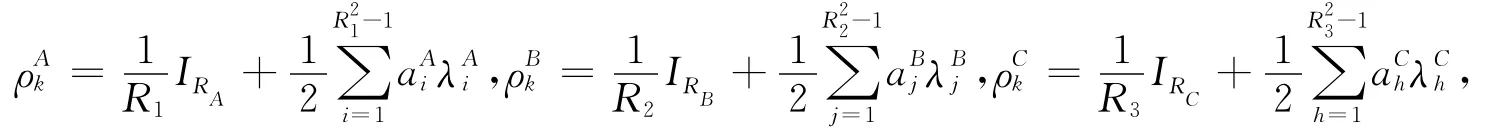
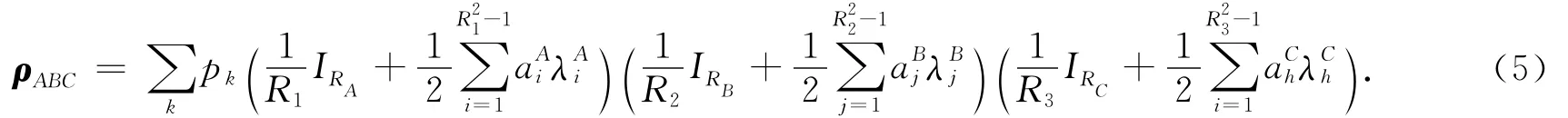
对比式(5)与定理2.2式子的系数可得

不妨设

则由引理1.2和迹范数的凸性可知

为了验证定理2.3的正确性,首先考虑Werner量子态.设Werner量子态的密度矩阵为ρ1,且

其中0≤p≤1.由文献[4]可知,对于 Werner态ρ1,当时,ρ1是可分的.
证明:量子态ρ的矩阵形式为

则由定理2.3得Γρ的形式为

故定理2.3得到验证.
3 结束语
首先,利用SU(R)群的R2-1个独立生成元和单粒子量子态的表示形式,给出三体量子系统密度矩阵所在线性空间的Hamel基,以及三体量子系统密度矩阵的表示形式.其次,利用量子态表示形式中的表示系数,构造表示系数矩阵.在此基础上,证明对任意三体量子系统密度矩阵ρABC,若ρABC是可分的,则其表示系数矩阵的Frobenius范数不超过1;若其表示系数矩阵的Frobenius范数大于1,则ρABC是纠缠的.最后,利用经典的Werner量子态,构造能够例证文中定理和推论的例子.
[1]Nielsen M A,Chuang I L.Quantum computation and quantum information[M].London:Cambridge University Press,2000.
[2]Thew R T,Nemoto K,White A G,et al.Qudit quantum-state tomography[J].Phys.Rev.A,2002,66(1):1-6.
[3]Werner R F.Quantum states einstein podolsk rosen correlations admitting a hidden-variable model[J].Phys.Rev.A,1989,40(8):4277-4281.
[4]Peres M.Separability criterion for density matrices[J].Phys.Rev.Lett,1996,77(8):1413.
[5]Horodecki M,Horodecki P.Reduction criterion of separability and limits for a class of distillation protocols[J].Phys.Rev.A,1999,59(6):4206.
[6]Rudolph O.Some properties of the computable cross-norm criterion for separability[J].Phys.Rev.A,2003,67(3):1-6.
[7]Zhao H,W Z X.Separability criteria for quantum mixed states[J].Commun.Theor.Phys,2004,42(10):529-532.
[8]Zhao H.Separability criteria for quantum mixed states in terms of trace norm[J].Chin.Phys.Lett.,2006,23(7):1674-1675.
[9]Li Ming,Fei Shaoming,Wang Zhixi.Separability and entanglement of quantum states based on covariance matrices[J].J.Phys A:Math Theor.,2008,(41):358-367.
[10]汪威威,毕红梅.两体量子态可分离性判据[J].西安工业大学学报,2008,28(10):414-416.Wang Weiwei,Bi Hongmei.The qubit quantum separability criterion[J].Journal of Xi’an Technological University,2008 ,28(10):414-416.
[11]汪威威,曹怀信.二元量子系统混态密度矩阵可分性研究[J].咸阳师范学院学报,2008,23(2):6-9.Wang Weiwei,Cao Huaixin.The density matrix separability of qubit system in mixed state[J].Journal of Xianyang Normal University,2008,23(2):6-9.
