页岩气藏数值模拟及井底压力动态分析

李清泉，王新海，尹 虎，任 飞，王珊珊，张 磊

（1.中国石油大学石油工程教育部重点实验室，北京 102249； 2.长江大学油气资源与勘探技术教育部重点实验室，湖北 荆州 434023； 3.塔里木油田公司，新疆 库尔勒 841000）

0 引言

页岩气藏是指主体位于暗色泥页岩或高碳泥页岩中，以吸附或游离状态为主要存在方式的天然气聚集，是目前天然气勘探的重要目标[1-2］，我国对页岩气藏的研究与勘探开发处于探索阶段[3］，人们对低渗透页岩气藏的地质条件、聚集机理和产能预测等方面进行研究[4］.段永刚等[5］考虑页岩气藏存在吸附解吸特性，运用点源函数及质量守恒法建立页岩气藏双重介质压裂井数学模型，并研究其渗流机理和产能评价；田冷等[6］应用渗透率模量概念建立存在应力敏感的气藏不稳定试井模型；程远方等[7］提出页岩气藏三孔双渗介质模型；宁正福等[8］应用渗透率模量概念，建立存在应力敏感的裂缝性双区复合气藏不稳定试井模型；目前同时考虑吸附气解吸及压力敏感性气藏模型方面的研究很少.针对页岩气藏同时具有吸附气解吸及压力敏感性质，笔者提出双孔双渗页岩气藏模型，分析井底压力与压力双对数曲线的影响因素.

1 页岩气解吸方程

页岩气吸附理论主要有单分子层吸附、多分子层吸附和吸附势等.页岩对甲烷等气体的吸附为单分子层吸附，吸附等温线为Ⅰ类，用兰缪尔方程[9-10］能较好地描述，表示为

吸附气解吸后以扩散形式进入裂缝，假设页岩气在扩散过程中每个时间段有唯一的平均页岩气浓度，在浓度差作用下，基质块中页岩气向外扩散，过程遵循Fick第一定律[11］，表示为

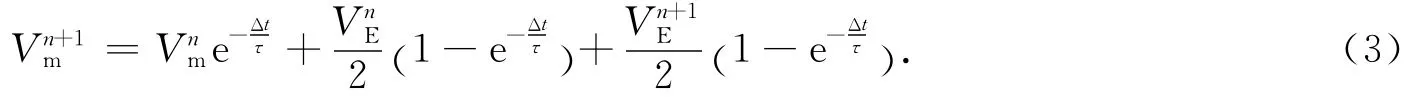
将式（3）代入式（2），得到解吸量[12］：

式（1～4）中：VE为平衡等温吸附量；VL为兰氏体积；p为系统压力；pL为兰氏压力；Vm为基质中的吸附气浓度；t为时间；τ为吸附时间；qm为解吸量；FG为形状因子；ρgm为基质系统中的气体密度；pm为基质系统压力.

2 渗透率压力敏感方程

随着流体产出，有效压力减小，地层渗透率减小.基质和裂缝系统的渗透率均为压力的函数，在压力敏感性储层，渗透率与压力变化近似呈指数关系[13］，可表示为

式（5）中：l为基质或裂缝，取为m或f；Kl为基质或裂缝系统的渗透率；Kli为基质或裂缝系统的原始渗透率；aKl为压力敏感系数，反映渗透率与净有效覆压的敏感程度，aKl越大，表示渗透率对净有效上覆压力越敏感；pli为基质或裂缝系统的原始压力；plg为基质或裂缝系统的压力.

3 数学模型

假设：（1）均质等厚圆形地层中心一口定产量生产井，产量为q；（2）单相气体、等温渗流且服从达西定律；（3）考虑双孔双渗模型，流体由裂缝和基质同时向井筒流动，由基质向裂缝窜流；（4）页岩气解吸服从兰缪尔定律；（5）忽略重力和毛细管力影响，考虑渗透率应力敏感影响.

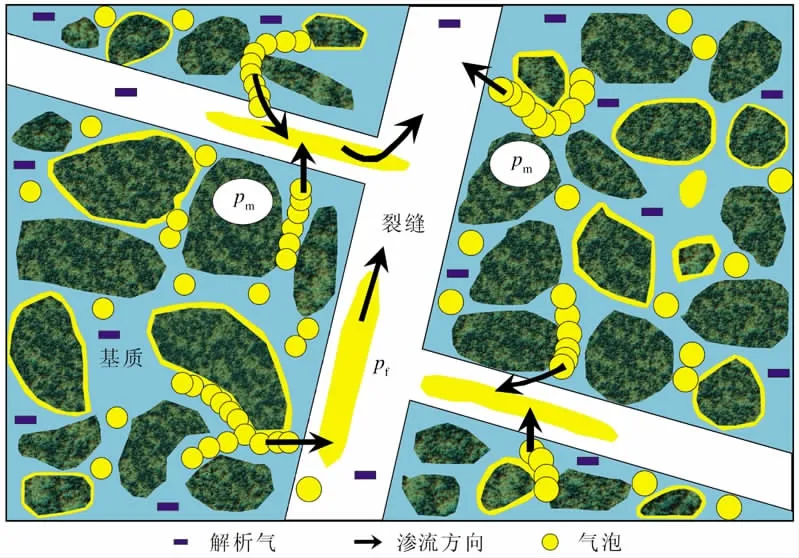
图1 页岩气渗流示意（pm＞pf）Fig.1 Shale gas flow diagram（pm＞pf）

裂缝渗流方程：

基质渗流方程：

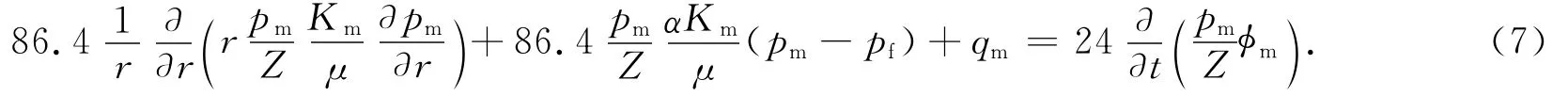
初始条件：

内边界条件：

外边界条件：

式（6～12）中：r为渗流半径；pf为裂缝系统压力；Z为天然气压缩因子；Kf为裂缝系统渗透率；μ为黏度；φf为裂缝系统孔隙度；α为形状因子；Km为基质系统渗透率；pi为原始地层压力；rw为井筒半径；pwf为井底压力；φm为基质系统孔隙度；B为天然气体积因数；C为井储系数；sf为裂缝系统表皮系数；sm为基质系统表皮系数；re为供给半径.

4 数值模型

根据数学模型，采用有限差分法建立对应的数值模型[14］.以井为中心，对渗流区域采用径向块中心网格，进行坐标变换：为径向上的网格数.

（1）裂缝渗流差分方程为

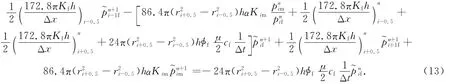
（2）基质渗流差分方程为

式（13～14）中：ri为单个网格渗流半径为拟压力函数为裂缝系统压缩系数；cm为基质系统压缩系数；当i＝1或i＝N时，式（13～14）需要修正.

式（13～14）可构成5对角矩阵，采用超松弛迭代法[15］求解，得到不同时刻、不同空间位置对应的裂缝及孔隙拟压力，进而求得相应的裂缝及孔隙压力，最后得到相应时刻的井底压力：

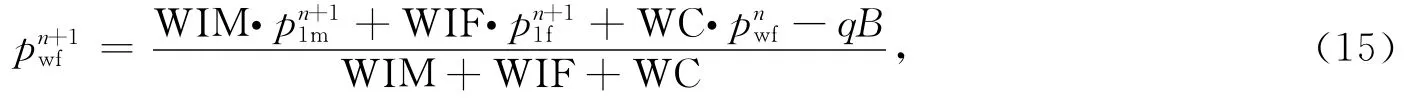
5 井底压力影响因素

根据数值模型计算得到以无因次时间tD／CD为横坐标的井底压力p及压力导数p′双对数曲线，分析参数对双对数曲线的影响.井底压力导数曲线分为6段：（1）井储直线段（前期斜率为1的部分）；（2）受表皮因数影响的“驼峰”段；（3）早期裂缝径向流段（第一水平段）；（4）基质向裂缝流动的窜流段（凹部）；（5）系统径向流段（第二水平段）；（6）封闭边界响应段（后期曲线上翘段）[16］.

5.1 解吸

解吸对井底压力双对数曲线的影响见图2.由图2可见：考虑解吸时窜流段下凹幅度更大，系统径向流段出现滞后，且较晚触到边界.这是因为考虑解吸时，随着基质中游离气的耗散，基质中的吸附气解吸出来变为游离气参与窜流并向井筒流动.吸附气解吸不仅影响试井解释参数准确性，而且影响气井产能预测结果，对于有吸附气的非常规气藏，必须考虑解吸的影响.

5.2 兰氏体积

兰氏体积为给定的温度条件下，页岩吸附甲烷达到最大饱和度时的吸附量，与页岩比表面积及被吸附的气体有关，不同页岩吸附量的差异，主要反映在兰氏体积不同上.兰氏体积对井底压力双对数曲线的影响见图3，由图3可见：兰氏体积越大，解吸效果越好，压降随时间的变化率也越小，表现为窜流段下凹程度加深.

图2 解吸对井底压力双对数曲线的影响Fig.2 Desorption＇s influence on double logarithm curve of bottom hole pressure

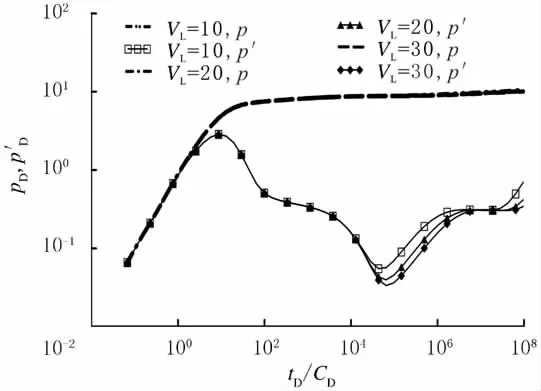
图3 兰氏体积对井底压力双对数曲线的影响Fig.3 Langmuir volume＇s influence on double logarithm curve of bottom hole pressure

5.3 兰氏压力

兰氏压力是吸附量达到极限吸附量50%时所对应的压力，即V＝0.5VL时，p＝pL.兰氏压力对井底压力双对数曲线的影响见图4，由图4可见：兰氏压力越接近地层压力，解吸效果越明显；越慢接触到边界，压力降落越缓慢.

5.4 吸附时间常数

吸附时间常数与扩散距离相关，表现为与裂缝间距的平方成正比.裂缝密度越大，页岩气扩散距离越短，吸附时间常数越小，扩散效果越好.吸附时间常数对井底压力双对数曲线的影响见图5，由图5可见：吸附时间常数分别为100，200，300h时的井底压降曲线及压力导数曲线，吸附时间常数越小，波谷段下凹程度越深，且越容易达到整体径向流段.这是由扩散效果变好、缩短窜流段造成的.

5.5 压力敏感系数

压力敏感系数对井底压力及压力导数双对数曲线的影响见图6.由图6可见：考虑压力敏感系数时，随着基质系统及裂缝系统压力的降低，基质系统及裂缝系统的孔隙度和渗透率也不同程度地降低，从而使得双对数曲线上翘，并且应力敏感系数越大，曲线上翘幅度越大.

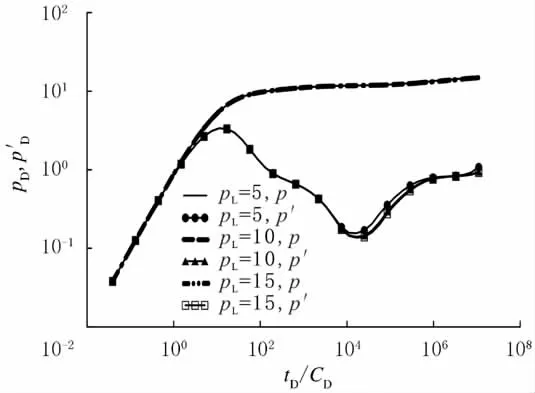
图4 兰氏压力对井底压力双对数曲线的影响Fig.4 Langmuir pressure＇s influence on double logarithm curve of bottom hole pressure

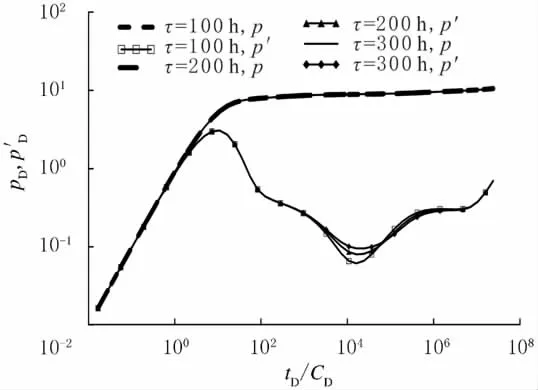
图5 吸附时间常数对井底压力双对数曲线的影响Fig.5 Adsorption time constant＇s influence on double logarithm curve of bottom hole pressure

图6 压力敏感系数对井底压力双对数曲线的影响Fig.6 Pressure sensitive coefficient＇s influence on double logarithm curve of bottom hole pressure

6 结论

（1）吸附气解吸对井底压力及压力导数双对数曲线有较大影响，页岩气井试井解释必须考虑解吸的影响.

（2）兰氏体积或兰氏压力越大，则窜流段曲线下凹幅度越大.

（3）吸附时间越短，扩散效果越好，气藏的整体径向流段越快达到，且径向流段时间越长.

（4）压力敏感系数系数越大，压力导数双对数曲线上翘幅度越大.

[1]张金川，薛会，张德明，等.页岩气及其成藏机理[J］.现代地质，2003，17（4）：466.Zhang Jinchuan，Xue Hui，Zhang Deming，et al.Shale gas and its accumulation mechanism[J］.Journal of Modern Geology，2003，17（4）：466.

[2]张金川，金之钧，袁明生.页岩气成藏机理和分布[J］.天然气工业，2004，24（7）：15-18.Zhang Jinchuan，Jin Zhijun，Yuan Mingsheng.The accumulation mechanism and distribution of shale gas[J］.Natural Gas Industry，2004，24（7）：15-18.

[3]张金川，徐波，聂海宽，等.中国页岩气资源勘探潜力[J］.天然气工业，2008，28（6）：136-140.Zhang Jinchuan，Xu Bo，Nie Haikuan，et al.The potential exploration of shale gas resource in China[J］.Journal of Gas Industry，2008，28（6）：136-140.

[4]胡文瑞.中国非常规天然气资源开发与利用[J］.大庆石油学院学报，2010，34（5）：9-16.Hu Wenrui.The development and utilization of unconventional gas resources in China[J］.Journal of Daqing Petroleum Institute，2010，34（5）：9-16.

[5]段永刚，魏明强，李建秋，等.页岩气藏渗流机理及压裂井产能评价[J］.重庆大学学报，2011，34（4）：62-65.Duan Yonggang，Wei Mingqiang，Li Jianqiu，et al.Percolation mechanism of shale gas reservoir and productivity evaluation of fractured well[J］.Journal of Chongqing University，2011，34（4）：62-65.

[6]田冷，何顺利，李秀生，等.低渗透气田砂岩储层应力敏感试井模型研究[J］.石油钻探技术，2007，35（6）：89-91.Tian Leng，He Shunli，Li Xiusheng，et al.Well testing model of stress sensitive low permeability gas reservoir in sandstone reservoir[J］.Journal of Oil Drilling Technology，2007，35（6）：89-91.

[7]程远方，董丙响，时贤，等.页岩气藏三孔双渗渗流机理[J］.开发工程，2012，82（9）：1-4.Cheng Yuanfang，Dong Bingxiang，Shi Xian，et al.Percolation mechanism of shale gas reservoir with triple-porosity and dual permeability system [J］.Development Engineering，2012，82（9）：1-4.

[8]宁正福，廖新维，高旺来，等.应力敏感裂缝性双区复合气藏压力动态特征[J］.大庆石油学院学报，2004，28（2）：34-36.Ning Zhengfu，Liao Xinwei，GaoWanglai，et al.Dynamic characteristics of pressure in stress sensitive gas reservoir with fractured double composite[J］.Journal of Daqing Petroleum Institute，2004，28（2）：34-36.

[9]Freeman C M，Moridis G，IK D，et al.A numerical study of performance for tight gas and shale gas reservoir systems[J］.SPE，2009，SPE124961.

[10]Salman A，Mengal，Wattenbarger R A.Accounting for adsorbed gas in shale gas reservoirs[J］.SPE，2011，SPE141085.

[11]段永刚，李建秋.页岩气无限导流压裂井压力动态分析[J］.天然气工业，2010，30（10）：1-4.Duan Yonggang，Li Jianqiu.Dynamic analysis of the pressure of infinite conductivity fractured well in shale gas reservoirs[J］.Journal of Natural Gas Industry，2010，30（10）：1-4.

[12]麻翠杰，郭大浩，邓英尔，等.致密煤层气运移的数值模拟[J］.大庆石油学院学报，2005，29（3）：13-15.Ma Cuijie，Guo Dahao，Deng Yinger，et al.Numerical simulation of dense coalbed methane migration[J］.Journal of Daqing Petroleum Institute，2005，29（3）：13-15.

[13]吴淑红，刘翔鹦，郭尚平.水平段井筒管流的简化模型[J］.石油勘探与开发，1999，26（4）：64-65.Wu Shuhong，Liu Xiangying，Guo Shangping.The simplified model of horizontal wellbore conduit flow section[J］.Petroleum Exploration and Development，1999，26（4）：64-65.

[14]张冬丽.煤层气定向羽状水平井开采数值模拟方法研究[D］.廊坊：中国科学院渗流流体力学研究所，2004.Zhang Dongli.Numerical simulation method of coalbed methane（CBM）with pinniform horizontal wells[D］.Langfang：The Chinese Academy of Sciences Institute of Seepage Fluid Mechanics，2004.

[15]徐士良.数值分析与算法[M］.北京：机械工业出版社，2007：68-71.Xu Shiliang.Numerical analysis and algorithm[M］.Beijing：Mechanical Industry Press，2007：68-71.

[16]Dominique Bourdet.现代试井解释模型及应用[M］.张义堂，译.北京：石油工业出版社，2007：102-103.Dominique Bourdet.Modern well testing interpretation model and application[M］.Translated by Zhang Yitang.Beijing：Petroleum Industry Press，2007：102-103.