基于自适应峰值分解的广义局部频率时频分析方法

王宪明，杨 枫，王 望，雷 娜，赵海峰

（1.东北石油大学 机械科学与工程学院，黑龙江 大庆 163318； 2.北京化工大学 机电工程学院，北京 100028； 3.中国石油天然气股份有限公司 大庆石化公司，黑龙江 大庆 163714）

0 引言

振动信号时频分析作为设备故障诊断特征提取的重要手段，在旋转机械故障诊断过程中发挥重要的作用.往复机械设备运动形式复杂、激励源多，传统的时频特征提取方法难以提取对应构件故障特征的频率成分，其振动以多源冲击信号为主体，在噪声的干扰作用下，振动信号表现较强的非平稳、非线性、非均匀、非光滑、非周期及非对称等复杂特性[1-4］.

传统频率概念[5］只对周期信号才有明确的物理意义；对于众多非周期信号，按照无限周期延拓得到的频率，缺乏频率含义，容易产生错误或交叉频率成分.非周期波动信号更具有广泛意义的波动形式，也有快慢与频率之分，只是频率及幅值以不断变化的形式出现，但全局频率概念无法对其进行有效描述，不得不将其排除在研究之外.虽然瞬时频率的概念[6］在HHT（希尔伯特黄变换）中得到较好利用；但是瞬时频率只适用于分析窄带信号，认为信号在每个瞬时时间点只存在一种频率成分，损失众多大尺度的频率信息，而且瞬时频率的物理意义缺乏清晰性，对众多信号不能进行瞬时频率计算[7］.

在故障诊断领域，旋转机械的典型故障又与信号谐波成分有很大关联度，得到较好的应用效果[8-12］.对于往复压缩机，将复杂的多源冲击信号进行谐波分解，时频分布变得非常复杂，许多频率成分缺乏明确的物理意义，虚假频率成分多，无法进行有效的故障特征提取[13］.因此，需要根据信号实测特性进行针对性的分解，给出明确物理意义的成分信息.

为了从往复压缩机多源冲击复杂信号中有效提取故障特征信息，根据多源冲击信号自身特点，在传统频率和瞬时频率尺度之间，提出一种广义局部频率的概念.通过仿真研究，分析其适用性，通过与自适应峰值分解方法结合，将其应用到往复压缩机气阀故障诊断中，为往复压缩机气阀故障诊断提供一种新手段.

1 基于广义局部频率的时频分析方法

1.1 基本概念

对于任意的一个零均值化离散时间序列x（i）（i＝1，2，…，n），其局部峰值反映该局部时间范围内振动的极限状态，因此可以作为判断振动完整周期起始标志的重要参考指标，提取x（i）所有的局部峰值，得到一个峰值时间序列p（i）（i＝1，2，…，n），即

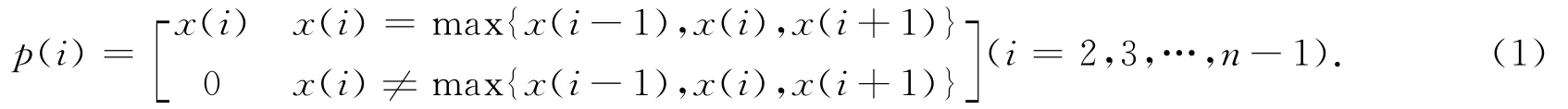
根据峰值时间序列p（i），可以给出时间尺度Ts和峰值尺度Ps定义，即

式中：a为时间尺度因子；b为峰值尺度因子；Fs为采样频率.

由式（1）定义可知，峰值序列p（i）中的非零值才是原序列x（i）所对应的局部峰值，为便于计算相邻峰值间隔，需要记录其在原序列中的相应位置，即

式中：m为峰值序列p（i）中的非零值个数，则相邻非零峰值的时间间隔数为m-1个，m-1个间隔可以组成序列Δ（k）（k＝1，2，…，m-1），即

给出峰值序列p（i）的时间间隔尺度Δs的定义，即

式中：c为时间间隔尺度因子.

在某一尺度组合（a，b，c）下，统计峰值序列p（i）的非零峰值个数，给出序列x（i）在该尺度组合下的广义局部频率υ，即

式中：t＊为所统计非零峰值的首尾所对应的时间长度；Ns为峰值序列p（i）的非零峰值个数，通过程序计数变量统计得到；Ns-1为出现完整振动周期的次数.

广义局部频率表征单位时间内出现完整周期的次数，与传统频率和瞬时频率的本质物理意义是一致的，即都是单位时间内振动快慢的衡量指标.从尺度上，传统频率考虑的是无限时长的尺度，瞬时频率考虑的是即时时长的尺度，分别在2种极端信号情况下才具有物理意义，缺乏普适性.广义局部频率是在2种尺度之间重新定义第三种更广义性的频率概念，它不仅考虑时间特征信息，而且还考虑幅值和时间间隔特征信息.

1.2 自适应峰值分解

在计算广义局部频率前，需要首先确定合适的3个尺度因子.对于峰值尺度因子b和时间间隔尺度因子c的确定方法相对困难，需要根据经验观察峰值的值域区间和时间间隔的值域区间特点给出，因此存在盲目性.为解决这个问题，提出一种自适应峰值分解的方法，其原理见图1.

（1）提取x（i）的局部极大值，得到第一个峰值序列p1（i）（i＝1，2，…，n）.

图1 自适应峰值分解原理Fig.1 Diagram of adaptive peak decomposition

（2）将峰值序列p1（i）作为新的时间序列x1（i），根据步骤（1），同理得到第二个峰值序列p2（i）（i＝1，2，…，n）.

（3）重复步骤（2），直至得到的峰值序列pm（i）（i＝1，2，…，n），满足非零的峰值个数小于或等于2结束.其中，m 为自适应峰值分解后全部峰值子序列的个数，即p1（i），p2（i），…，pm（i）.

由图1可知，对于任意的一个零均值化离散时间序列x（i）（i＝1，2，…，n），通过重复提取局部极大值的方法，能被分解为m 层峰值子序列p1（i），p2（i），…，pm（i），各峰值子序列蕴含不同时间间隔尺度及不同幅值尺度下的频率及其相应能量信息.

2 仿真结果分析

往复压缩机振动信号具有多源冲击特性，结合实际工况中所包含常见振动信号特点，分别以幅度调制信号为例进行仿真分析，将基于自适应峰值分解的广义局部频率时频分析与基于EMD的HHT时频分析进行对比，研究广义局部频率概念的适用性及有效性，为往复压缩机时频故障特征提取提供依据[14-15］.

其中时间t＝0～6s，特征频率分别为2Hz和10Hz，采样频率Fs＝100Hz，基于自适应峰值分解的广义局部频率时频分析结果见图2.基于EMD分解的HHT时频分析结果见图3.

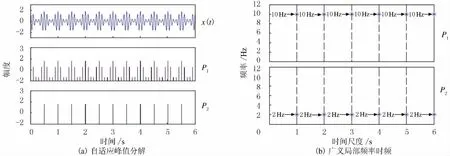
图2 幅度调制信号广义局部频率时频分析Fig.2 Time-frequency analysis of amplitude modulated signal based on general local frequency

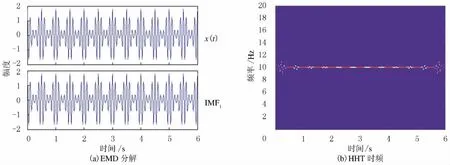
图3 幅度调制信号HHT时频分析Fig.3 Time-frequency analysis of amplitude modulated signal based on HHT

由图2可以看出，幅度调制信号被自适应峰值分解为P1和P2两个尺度，其广义局部频率分别为10 Hz和2Hz，与原信号特征频率吻合.由图3可以看出，幅度调制信号被EMD分解为1个固有模态.虽然分解结果不存在趋势干扰项，但是IMF1与原信号相同，相比于自适应峰值分解，其分解后信号的物理意义不够清晰，幅度调制信号的HHT时频分析只提取特征频率10Hz，未能提取到特征频率2Hz.此外，其瞬时频率存在明显的端部效应，比较而言，广义局部频率在时间尺度范围内计算频率结果更稳定，物理意义更清晰.

3 往复压缩机气阀实测信号时频分析

为采集不同状态下的往复压缩机振动试验数据，在大庆天然气公司南区压气站1号工作机组的二级气缸上安装正常状态及阀片有缺口状态的气阀，进行故障模拟试验，加速度传感器布置在气阀阀盖上，采样频率为50kHz，采样时间为0.4s.气阀正常状态及阀片有缺口状态下振动信号的时域波形见图4.

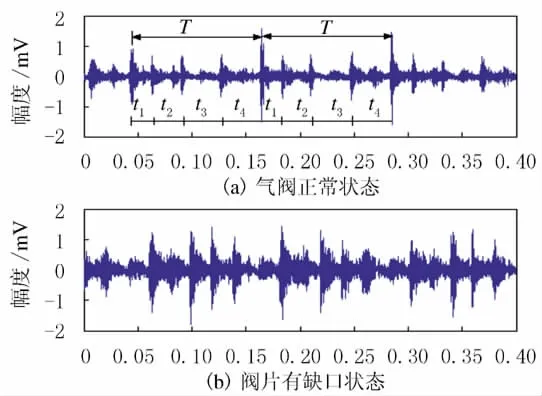
图4 正常状态和阀片有缺口状态下气阀振动信号时域波形Fig.4 Time waveform of gas vlave signal in two states

由图4可知，在气阀正常状态下，信号循环周期T＝0.12s，即特征频率为8.3Hz.气缸在一个周期内有4个循环过程：排气、膨胀、吸气及压缩，对应所需时间t1＝0.02s，t2＝0.025s，t3＝0.04s及t4＝0.037s，即特征频率为50Hz，40Hz，25Hz及27Hz.阀片有缺口故障状态下，特征不明显.此外，时域波形也无法提取2种状态下信号冲击时的高频特征，因此需要通过其他方法进一步分析.

将基于自适应峰值分解的广义局部频率时频方法应用于2种状态下的气阀振动信号，分析结果见图5和图6.由图5～图6可知，2种状态下气阀信号自适应峰值分解为7个峰值序列，但阀片有故障状态下P7少于2个峰值，因此只能对前6个峰值序列进行广义局部频率计算.在峰值尺度P5～P6下能提取到特征频率50Hz，40Hz，25Hz及27Hz；在峰值尺度P1～P3下的高频特征相同；在峰值尺度P4下存在一定差异，正常状态时特征频率为70～250Hz，而阀片有缺口状态时特征频率为100～300Hz，可以作为往复压缩机气阀故障特征的依据.

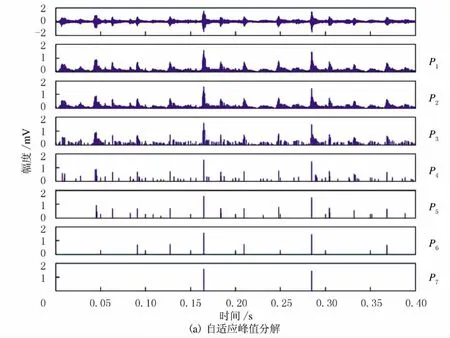
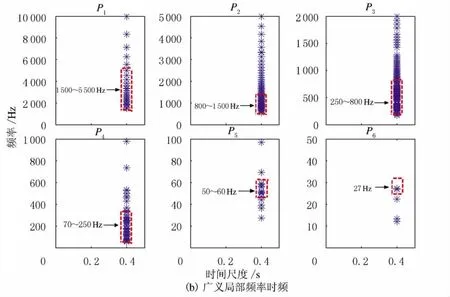
图5 气阀正常状态下信号广义局部频率时频分析Fig.5 Time-frequency analysis of normal valve signal based on general local frequency

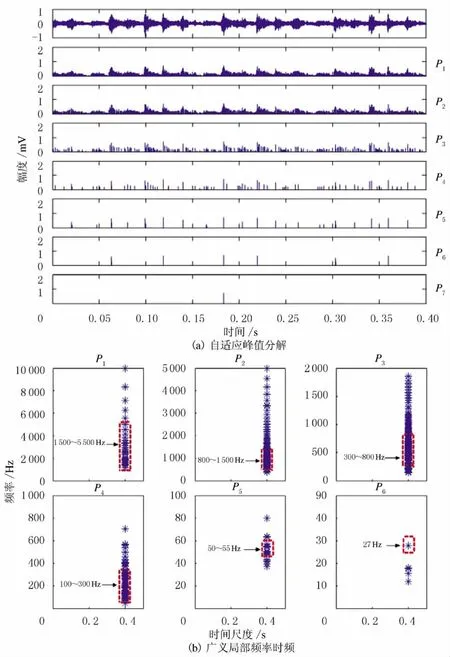
图6 阀片有缺口状态下信号广义局部频率时频分析Fig.6 Time-frequency analysis of gap valve signal based on general local frequency

4 结论

（1）提出广义局部频率概念，从时间尺度、峰值尺度及时间间隔尺度进行定义，包含2种极限尺度下的传统频率和瞬时频率.

（2）自适应峰值分解方法能够给出合理的峰值尺度及时间间隔尺度划分原则，为广义局部频率的计算提供依据.

（3）基于自适应峰值分解的广义局部频率时频分析方法具有良好的自适应性，分解结果完全独立，各峰值子序列所含频带成分独立，频带成分由高到低进行变化，不存在重复或交叉干扰项，物理意义清晰，具有广泛适用性和有效性.

（4）基于自适应峰值分解的广义局部频率方法更加有效揭示往复压缩机多源冲击振动信号的时频特征信息，为往复压缩机故障诊断提供一种新手段.

[1]Liu Shulin，Tang Youfu，Liu Jicheng，et al.Research of fault feature extraction based on high order cyclic statistics for reciprocating compressor gas valves[J］.Applied Mechanics and Materials，2011，44／47：2094-2098.

[2]丛蕊，高学良，刘树林，等.EMD和关联维数在往复压缩机故障诊断中的应用[J］.大庆石油学院学报，2008，32（2）：86-89.Cong Rui，Gao Xueliang，Liu Shulin，et al.Application to fault diagnosis of reciprocating compressor based on emprical mode decomposition and correlation dimension[J］.Journal of Daqing Petroleum Institute，2008，32（2）：86-89.

[3]窦唯，于楷，孟庆武，等.基于免疫系统机理对距离函数故障诊断方法的改进[J］.大庆石油学院学报，2003，27（3）：54-56.Dou Wei，Yu Kai，Meng Qingwu，et al.The improvement of the fault diagnosis of distance function based on immune systems mechanism[J］.Journal of Daqing Petroleum Institute，2003，27（3）：54-56.

[4]刘树林，崔军明，林雪源，等.反面选择算法与神经网络相结合的故障诊断方法[J］.大庆石油学院学报，2005，29（6）：104-106.Liu Shulin，Cui Junming，Lin Xueyuan，et al.Fault diagnosis approach based on negative selection algorithm and neural network[J］.Journal of Daqing Petroleum Institute，2005，29（6）：104-106.

[5]Roberts M J.Signals and systems：analysis using transform methods and MATLAB[M］.McGraw-Hill，America，2004.

[6]Jonathan M L，Sofia C O.Bivariate instantaneous frequency and bandwidth[J］.IEEE Transactions on Signal Processing，2010，58（2）：591-603.

[7]Laila D S，Messina A R，Pal B C.A refined Hilbert-Huang transform with applications to interarea oscillation monitoring[J］.IEEE Transaction on Power Systems，2009，24（2）：610-620.

[8]何正嘉，訾艳阳，陈雪峰，等.内积变换原理与机械故障诊断[J］.振动工程学报，2007，20（5）：528-533.He Zhengjia，Zi Yanyang，Chen Xuefeng，et al.Transform principle of inner product for fault diagnosis[J］.Journal of Vibration Engineering，2007，20（5）：528-533.

[9]Dou W，Liu Z S.Genetic integration of different diagnosis methods and／or fault features for improvement of diagnosis accuracy[J］.Journal of Vibration and Acoustics-Transactions of the ASME，2009，131（1）：011002.1-011002.8.

[10]Lei Yaguo，He Zhengjia，Zi Yanyang.Application of the EEMD approach to rotor fault diagnosis of rotating machinery[J］.Mechanical Systems and Signal Processing，2009，23（4）：1327-1338.

[11]赵海峰，刘树林，齐波，等.基于经验模态分解及自相关分析的微弱信号提取方法[J］.大庆石油学院学报，2007，31（5）：80-84.Zhao Haifeng，Liu Shulin，Qi Bo，et al.Approach to weak signal extraction based on empirical mode decomposition and autocorrelation analysis[J］.Journal of Daqing Petroleum Institute，2007，31（5）：80-84.

[12]刘树林，赵海峰，王辉，等.局部频率概念及适用性分析[J］.振动与冲击，2008，27（s）：202-204.Liu Shulin，Zhao Haifeng，Wang Hui，et al.Local frequency concept and its adaptivity[J］.Journal of vibration and shock，2008，27（s）：202-204.

[13]谭继勇，陈雪峰，何正嘉.冲击信号的随机共振自适应检测方法[J］.机械工程学报，2010，46（23）：61-66.Tan Jiyong，Chen Xuefeng，He Zhengjia.Impact signal detection method with adaptive stochastic resonance[J］.Journal of Mechanical Engineering，2010，46（23）：61-66.

[14]Huang NE，Shen Z，Long S R.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J］.Proceedings of the Royal Society of London，1998，454：903-995.

[15]Liu Yukun，Guo Liwei，Wang Qixiang.Application to induction motor faults diagnosis of the amplitude recovery method combined with FFT[J］.Mechanical Systems and Signal Processing，2010，24（8）：2961-2971.