时标上三阶中立型动力方程的振动性与渐近性

尚仲平

（燕山大学继续教育学院，河北秦皇岛 066004）

时标上动力方程的研究可追溯到其创立者Hilger［1］，是当前国内外学者极为关注的新研究热点.因为时标分析理论不仅能够统一连续分析和离散分析，而且有着广泛的应用背景.许多领域提出了大量这类的问题，例如：生态领域、自动控制领域、信息领域以及经济领域等［2］.近几年，时标上动力方程振动性的研究也取得了许多结果，如Saker等［3－8］讨论了时标上二阶动力方程的振动性，Li［9］研究了时标上一阶中立型时滞微分方程的振动性，最近Hassan［10］又研究了时标上三阶动力方程的振动性.但是上述文献［3－7］所考虑的时标上的动力方程均不是中立型或变时滞的，本文所研究的动力方程更具广泛性，同时在处理一些细节问题时采用了不同的方法，所得新结果推广并发展了现有的一些结论.

首先给出一些基本的定义，见文献［2］.

时标T是指实数R上的一个非空子集，对任意T，定义向前跳跃算子σ和graininess函数μ分别为σ（t）：＝inf｛s∈T：s＞t｝，μ（t）：＝σ（t）－t.当σ（t）＝t时，称t是右稠密的，当σ（t）＞t时，称t是右稀疏的.类似的，可定义向后跳跃算子e（t）∶＝sup｛s∈T：s＜t｝，以及左稠密、左稀疏.

称函数f：T→R是rd－连续的，如果它在T上的右稠密点是连续的，且在T上的左稠密点左极限存在（为有限值），并记f∈Crd.

如果存在函数F（t），使得（t）＝fε（b），则定义s＝Fε（b）－Fε（a）.

关于时标上各种计算公式，请读者参阅文献［2］，本文不再列出.

本文考虑以下时标上三阶非线性中立型变时滞动力方程

的振动性与渐近性，在此考虑的时标T是无上界的，即T具有［t0，∞）形式.其中β≥1是正奇整数的商，ε≥0，c≥0，c（t），a（t），p（t）是定义在T上的正实值rd－连续函数.

方程（1）的一个解x（t）称为振动的是指它既不最终为正，也不最终为负，否则称它为非振动（渐近）的.如果一个方程的所有解是振动的，就说该方程是振动的.

如果方程（1）是振动的或者是渐近的需要有以下3个条件成立：

（H1）时滞函数r（t）：T→T和τ（t）：T→T满足且（τ·σ）（t）＝（σ·τ）（t）；

（H2）0≤p（t）＜1；

（H3）函数fε：T×R→R满足ufε（t，u）＞0，并且存在时标T上正的rd－连续函数qε（t）使得

1 预备知识

引理1 假设x（t）是方程式（1）的一个最终正解，且下面的条件成立

则存在一个t1∈［t0，∞）使得：Ⅰ）y（t）＞0，yΔ（t）＞0，（a（t）yΔ（t））Δ＞0，t≥t1或Ⅱ）y（t）＞0，yΔ（t）＜0，（a（t）yΔ（t））Δ＞0，t≥t1成立.

证明 令

设x（t）是方程（1）一个最终正解，则存在t1≥t0使得x（t）＞0，x（r（t））＞0，x（τ（t））＞0，t≥t1.由式（4）得y（t）＞0，t≥t1.再由式（1）和（2）得

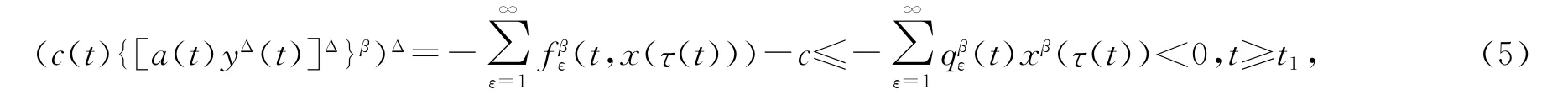
这表明c（t）｛［a（t）yΔ（t）］Δ｝β在［t1，∞）是严格单调减少的，下面证明c（t）｛［a（t）yΔ（t）］Δ｝y＞0，t≥t1.否则，则存在t2≥t1，使得c（t）｛［a（t）yΔ（t）］Δ｝β≤d＜0，t≥t2.那么两边同除以c（t）并开方，再从t2到t积分得

由式（3）知，当t→∞时，a（t）yΔ（t）→－∞，从而存在t3≥t2和负常数e，使得a（t）yΔ（t）≤e＜0，t≥t3，则有yΔ（t）≤e／a（t），t≥t3，对该式从t3到t积分得

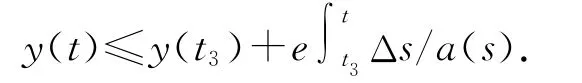
当t→∞时，y（t）→－∞.这与y（t）＞0，t≥t1矛盾，因此c（t）｛［a（t）yΔ（t）］Δ｝β＞0，t≥t1.这意味着［a（t）yΔ（t）］Δ＞0，故a（t）yΔ（t）在［t1，∞）是严格单调增加的，从而有yΔ（t）＞0或yΔ（t）＜0.证毕.引理2 假设x（t）是方程（1）的解并满足引理1中（Ⅱ），则存在t1∈［t0，∞）使得

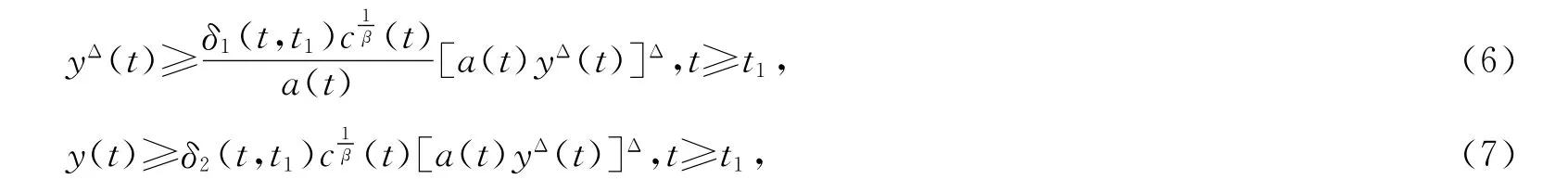
证明 因为c（t）｛［a（t）yΔ（t）］Δ｝β在［t1，∞）是严格单调减少的，所以

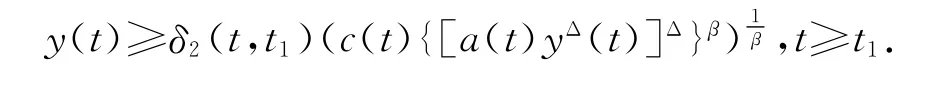
证毕.

引理3 假设

并且x（t）是方程（1）的解，且满足引理1中的（Ⅱ），则有.

证明 设x（t）是方程（1）的解，且满足引理1中（Ⅱ），即y（t）＞0，yΔ（t）＜0，（a（t）yΔ（t））Δ＞0，t≥t1，则＝b≥0.下面证明b＝0，假设b＞0，从式（4）知存在t2≥t1，使得x（τ（t））≥b／2，t≥t2，且存在一个q（t）使得

从t2到t积分知当t→∞时，有c（t）｛［a（t）yΔ（t）］Δ｝β→－∞，与c（t）｛［a（t）yΔ（t）］Δ｝β＞0矛盾，所以又因为0＜x（t）≤y（t），所以

2 主要结果

定理1 假设式（4）和式（9）成立，且存在一个正的函数ψ使得ψΔ在［t0，∞）上是rd－连续的，则对充分大的t1∈［t0，∞），

其中δ（τ（s），t1）∶＝δ1（τ（s），t1）（δ2（τ（s）），则方程（1）的所有解振动，或渐近趋于零.

证明 假设方程（1）有一个非振动解x（t）.不失一般性，则存在t1∈［t0，∞），使得x（t）＞0，x（r（t））＞0和x（τ（t））＞0，t≥t1.由引理1知，或者条件（Ⅰ）成立，或者条件（Ⅱ）成立.如果条件（Ⅱ）成立，由引理3得limx（t）＝0.如果（Ⅰ）成立，有

t→∞

由式（4）得y（t）＝x（t）＋p（t）x（r（t））≤x（t）＋p（t）y（r（t））≤x（t）＋p（t）y（t），从而x（t）≥（1－p（t））y（t）.根据式（1）和式（2）有

定义广义Riccati变换

则

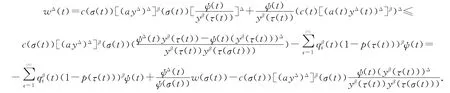
利用链式法则，知（yβ（τ（t）））Δ≥β（yβ－1（τ（t）））yΔ（τ（t））τΔ（t），所以

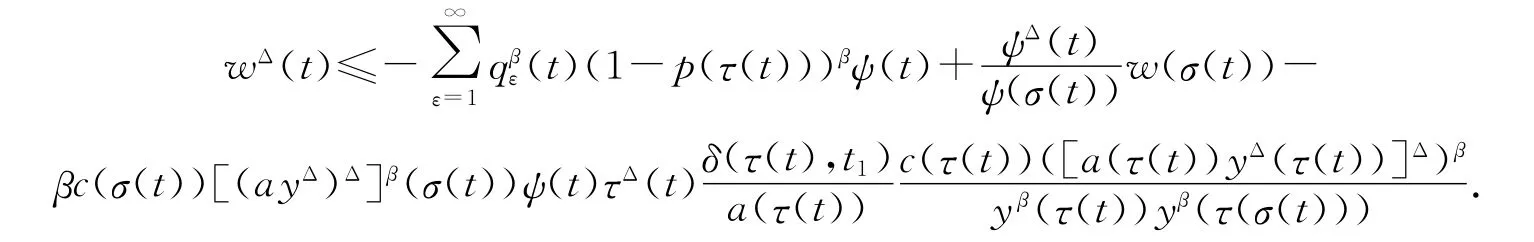
因为yΔ（t）＞0，τΔ（t）≥0，所以y（τ（σ（t）））≥y（τ（t））.又由于（c（t）｛［a（t）yΔ（t）］Δ｝γ）Δ≤0，因此c（τ（t））［（a（τ（t））yΔ（τ（t）））Δ］β≥c（σ（t））［（ayΔ）Δ］β（σ（t）），应用这2个不等式，

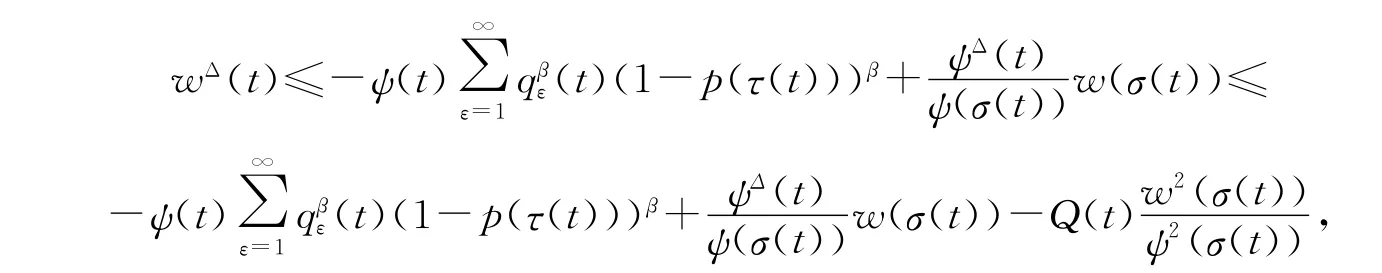
所以

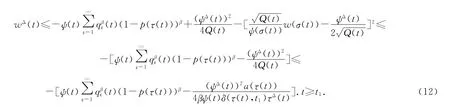
从t1到t积分得

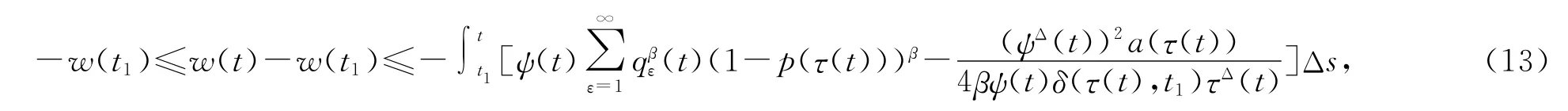
当ψ（t）＝t和ψ（t）＝1时，相应得到以下2个推论.

推论1 假设式（3）和式（9）成立，对充分大的t1∈［t0，∞），有

成立，则方程（1）的所有解振动，或渐近趋于零.

推论2 假设式（3）和式（9）成立，对充分大的t1∈［t0，∞），

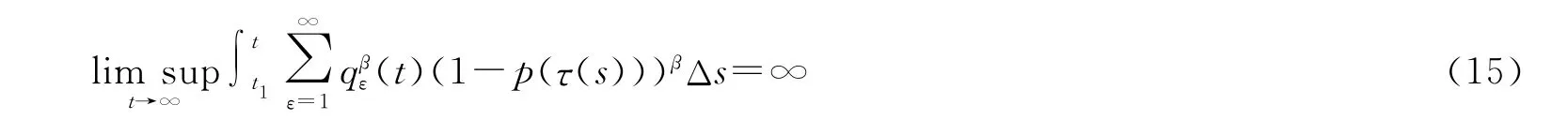
成立，则方程（1）的所有解振动，或渐近趋于零.

3 例子

本节利用例子对所得结果进行论证.考虑如下动力方程

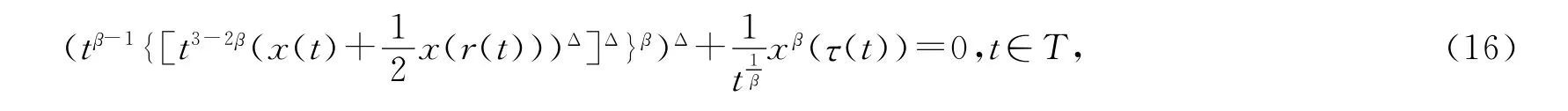
其中β≥1是正奇整数的商，这里取，c＝0并设条件（H1）成立，显然条件（H2），（H3）已满足.

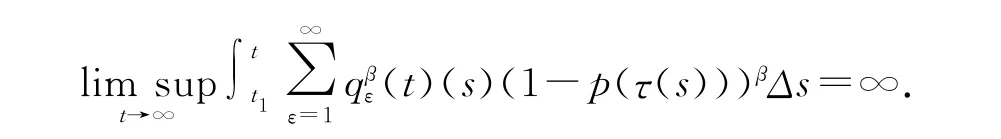
因此，由推论2可知方程（16）的所有解振动，或者渐进趋于零.

［1] HILGER S.Analysis on measure chains－a unified approach to continuous and discrete calculus［J］.Results Math，1990，18（1）：18－56.

［2] BOHNER M，PETERSON A.Dynamic equations on time scales：an introduction with applications［M］.Boston：Birkhuser，2001

［3] SAKER S H.Oscillation criteria of second－order half－linear dynamic equations on time scales［J］.J Comp Appl Math，2005，177（2）：375－387.

［4] SAKER S H.Oscillation of second－order nonlinear neutral delay dynamic equations on time scales［J］.Math Anal Appl，2006，187（2）：123－141.

［5] SAHINER Y.Oscillation of second－order delay differentialequations on time scales［J］.Nonlinear Analysis，2005，63（5－7）：1073－1080.

［6] ERBE L，PETERSON A，SAKER S H.Oscillation criteria for second－order nonlinear delay dynamic equations［J］.J Math Anal Appl，2007，333（1）：505－522.

［7] ERBE L，HASSAN T S，PETERSON A.Oscillation criteria for nonlinear damped dynamic equations on time scales［J］.Appl Math Comp，2008，203（1）：343－357.

［8] HASSAN T S.Oscillation criteria for half－linear dynamic equations on time scales［J］.Math Anal Appl，2008，345（1）：176－185.

［9] LI Yumei，WANG Youbin.Oscillation of first order neutral delay differential equations［J］.Journal of Wenzhou University：Natural Sciences，2007，26（6）：12－16.

［10] HASSAN T S.Oscillation of third order nonlinear delay dynamic equations on time scales［J］.Math Comp Model，2009，49（7－8）：1573－1580.