RC框架梁柱节点的静力非线性有限元分析

张瑞雪，阎红霞

（河北大学建筑工程学院，河北保定 071002）

钢筋混凝土（RC）框架结构的抗地震倒塌能力与其破坏机制密切相关.实验研究表明：梁端屈服框架的抗震性能较好，而柱端屈服型框架易形成倒塌机制.为了实现梁端屈服机制，中国框架结构设计中采用了一定的超配钢筋（包括楼板的配筋）和钢筋超强的柱端弯矩增大系数人为使柱端弯矩承载力大于框架梁端［1］.

汶川里氏8.0级特大地震的震后调研［2－3］发现：破坏的框架结构主要呈现“强梁弱柱”的破坏形式，见图1，“强柱弱梁”的屈服机制几乎没有出现，造成该现象的一个主要原因为框架结构抗震设计和分析中考虑现浇楼板对框架梁影响不够全面引起的［4－5］，故研究板筋对框架梁端承载力的影响迫在眉睫.研究可以采用实验或者数值模拟，其中实验方法费时费工，且仅针对几个或几组构件，较难得到普遍的结论；而数值模拟方法可以得到较多工况，但准确性很难保证.针对该问题本文采用ABAQUS有限元软件，对钢筋混凝土模型的材料本构的定义、钢筋的模拟、网格的划分等关键性问题进行了详细的叙述，并对有、无现浇楼板的2个框架节点进行了数值模拟，并和实验结果进行对比，验证了数值分析的正确性，为后续进一步研究框架结构屈服机制提供了合理的技术手段.

图1 “柱铰机制”破坏Fig.1 “Column hinge mechanism”damage

1 有限元的计算模型

图2a为RC框架结构在水平地震作用下的弯矩图，选取具有代表性的图2b所示虚线包围的中节点（相邻层和跨度间梁柱反弯点间，表示柱顶的恒定轴向力，表示梁加载端荷载）为研究对象.

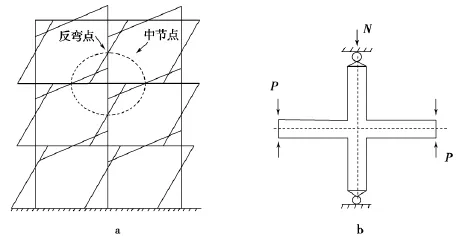
图2 RC框架在水平地震作用下的弯矩Fig.2 RC frame moments under horizontal seismic force

中节点尺寸［6－7］如图3所示，并采用“强柱弱梁”设计方法进行配筋，使梁端抗弯承载力为柱端的1.3倍（其中梁端负弯矩承载力未考虑板筋的作用），左右两侧分别为无楼板的中节点（构件1）和梁与板整浇的中节点（构件2），并且2试件中的梁、柱的尺寸和配筋相同.梁柱混凝土采用C30，节点核心区采用C50（图3立面图中的虚线范围）；梁柱主筋和板筋采用HRB338，梁柱箍筋采用HPB235.

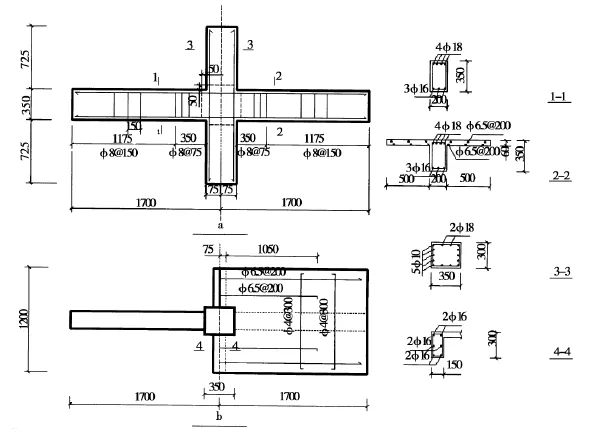
图3 2试件的几何尺寸以及配筋Fig.3 Plan of two test model size and reinforcement

1.1 有限元模型建立

1.1.1 模型介绍

在有限元软件ABAQUS中，对图3的中节点进行建模，有限元模型如图4所示（模型a，b分别对应构件1和2）.在有限元模型中，钢筋和混凝土采用分离式建模.具体如下：混凝土都采用实体C3D8R单元，如图4所示；钢筋采用仅考虑拉压应力T3D2单元，如图5所示；采用有限元ABAQUS中的Embedded方法把钢筋埋入到混凝土中.

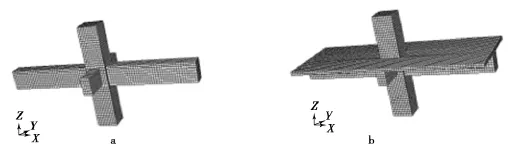
图4 2构件的有限元模型Fig.4 Finite element model of two members

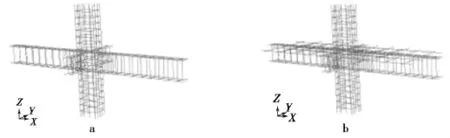
图5 2构件的钢筋骨架示意Fig.5 Steel skeleton diagram of two members

1.1.2 边界条件和加载方式

按照图1b所示，对有限元模型建立边界条件和加载方式.

1）边界条件：框架柱顶部和底部为反弯点，因此在有限元模型中约束了柱顶x，y方向的位移和x，z方向的转动，而柱底处的铰支座除了y方向以外的其余自由度都被约束；同时，节点左右的梁端为反弯点，因此在梁端限制其x，z方向的转动，节点仅在xz平面内发生位移.

2）加载方式：通过在柱顶施加竖向压力模拟柱顶轴压荷载（在柱顶按轴压比为0.2施加了压力570kN）；为了保证有限元计算的收敛，梁端竖向荷载采用位移加载的方式模拟.

1.1.3 材料的本构关系

1）钢材

钢材的应力－应变关系，采用双折线随动强化模型，如图6所示，其中Es为钢材弹性模量；fy，fu分别为钢材的屈服强度和极限强度；钢材弹塑性阶段后，具有一定的强化特性，钢材强化阶段的模量为αEs，通常系数α＝0.01.在钢材达到抗拉强度后，钢材强度不再增加.

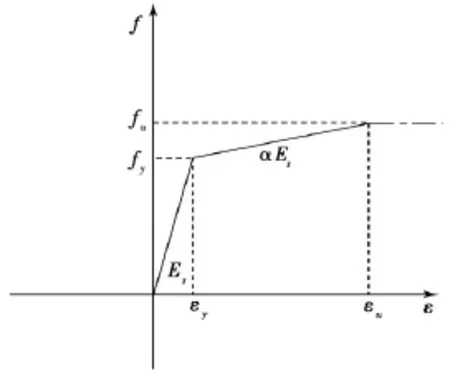
图6 钢材应力－应变关系曲线Fig.6 Stress－strain curve of steel

2）混凝土

混凝土采用混凝土塑性损伤模型，该模型最早由学者Lubliner等提出，学者Lee和Fenves进行了修改.该模型基于Drucker－Prager流动面的非关联流动，屈服面偏平面上的投影接近三角形，更加符合混凝土的特性.在使用中，该模型需要输入混凝土单轴受压、受拉的应力－应变关系.本文研究的构件涉及约束混凝土和非约束混凝土，下面分别介绍这2类混凝土的单轴受压、受拉的应力－应变关系.

a约束混凝土

对于约束混凝土的压应力－应变关系，本文选取可同时考虑纵、横向钢筋对混凝土约束效应的影响的Légeron＆Paultre模型［8］，如图7所示.

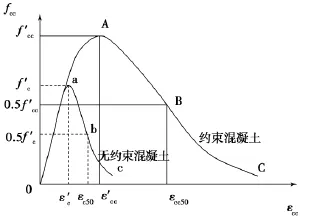
图7 混凝土单轴受压的应力－应变关系曲线Fig.7 Stress－strain curve of uniaxial compression concrete

应力－应变关系曲线表达式

其中，f′cc和ε′cc分别为约束混凝土受压峰值应力和峰值应变；fcc和εcc分别为约束混凝土压应力和压应变；k，k1和k2为控制参数.

式3和式4定义了约束混凝土受压峰值应力和峰值应变.

对于混凝土构件为矩形截面

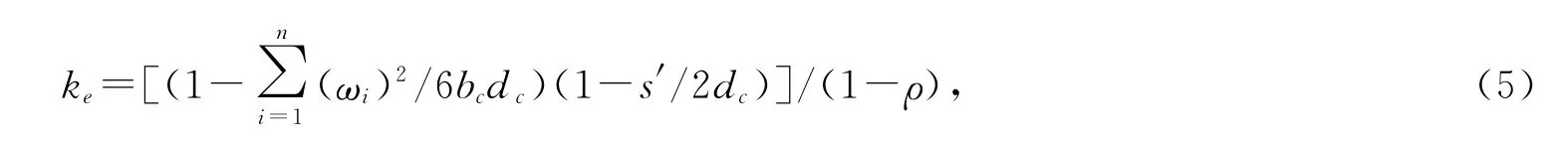
式中，fh为箍筋的应力；ke是有效配箍参数，ρsey0是体积配箍率；ρsey为有效体积配箍率；ρ是截面纵筋的配筋率；f′c为无约束混凝土受压峰值应力；n是矩形截面纵筋数；其余符号意义参见图8 .

图8 矩形截面混凝土受箍筋约束示意Fig.8 Rectangular cross－section bound by the stirrups

通过式6确定了约束混凝土的峰值压应力和应变与有效约束指标之间的关系

其中，f′c和ε′c分别为无约束混凝土的受压峰值应力和对应的应变，I′e为约束混凝土达到受压峰值应变ε′cc时的有效约束指标，即取fh＝fhcc按Ie＝ρseyfh／f′c计算，而fhcc按式7计算

其中，fhy为箍筋屈服强度；Esh为箍筋的弹性模量；参数m＝f′c／（ρseyEshε′c）.当混凝土无约束时，I′e＝0.

控制参数按式8和式9确定.

其中，εcc50为混凝土压应力是峰值应力50%时的压应变；Ect为混凝土弹性模型；各项指标可以参见图7.

b非约束混凝土

对于钢筋混凝土现浇楼板中的普通混凝土的应力－应变关系采用我国现行的混凝土单轴受压和受拉的应力－应变关系，参见文献［9］建议的曲线（图9所示），具体表达式见式10和式11.

式中，x＝ε／εc；y＝σ／f＊c，f＊c是混凝土单轴抗压强度，εc是对应的压应变，具体可参见混凝土规范［9］中的表C.2.1.

aa和ad分别是压应力－应变曲线的上升段和下降段的参数，按混凝土规范［9］表C.2.1.

式中，x＝ε／εt；y＝σ／f＊t；f＊t和εt分别为混凝土单轴抗拉强度和对应的峰值应变；at为单轴受拉应力－应变曲线下降段的参数值，其值和混凝土强度相关，可参见混凝土规范［9］表C.2.2.

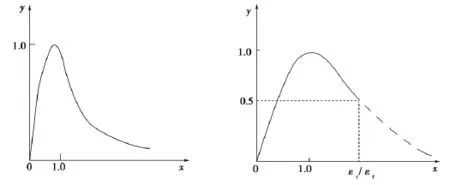
图9 混凝土单轴的应力－应变曲线Fig.9 Uniaxial stress－strain curve of concrete

图3所示的框架梁柱配筋，以及1.1.3所述的约束和非约束混凝土本构关系的定义，得到C30的单轴应力－应变关系曲线，如图10所示，约束混凝土的极限压应力较非约束混凝土提高了将近40%，可见不容忽视.

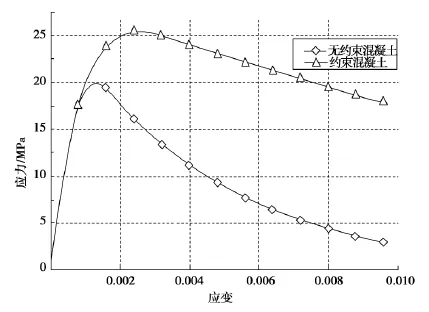
图10 混凝土单轴受压的应力－应变曲线Fig.10 Concrete compression stress－strain carve

2 验证有限元模型

框架梁的端荷载（P）－位移（Δ）是节点试件在往复荷载作用下力学性能的综合体现，限于篇幅，仅以构件2为例，图11是实验和有限元模拟2者的对比.根据参考文献［10］的方法确定构件屈服荷载，确定的实验和数值模拟的结果见表1.

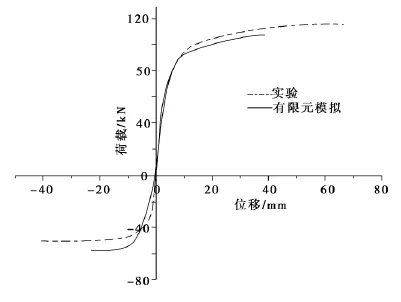
图11 梁端荷载－位移曲线Fig.11 Beam ends load－displacement curves

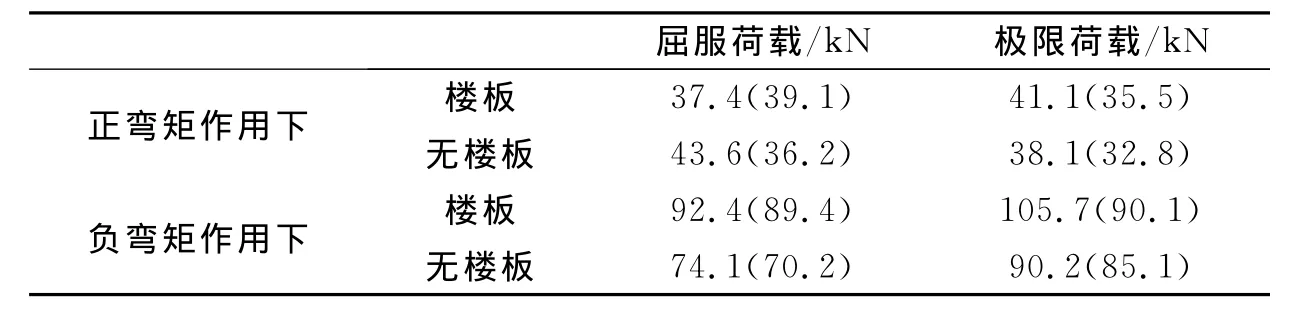
表1 实验和数值计算结果对比Tab.1 Comparison of test and numerical results

3 结论

1）现浇楼板对钢筋混凝土框架节点的影响非常大，提高了梁的抗负弯承载力，改变了梁柱的抗弯承载力差有可能改变框架结构“强柱弱梁”的屈服机制.

2）采用ABAQUS可以很好地模拟框架结构节点在静力荷载作用下的情况，并且计算出节点的屈服、极限荷载，延性；埋入钢筋技术可完成结构的精细建模，有效地提高了建模效率，后续将采用该有限元模拟方法进一步研究框架结构屈服机制.

［1] GB 50011—2010建筑抗震设计规范［S］.北京：中国建筑工业出版社，2010.

［2] 王亚勇.汶川地震建筑震害启示—抗震概念设计［J］.建筑结构学报，2008，29（4）：20－25.WANG Yayong.Lessons learnt from building damages in the Wenchuan earthquake—seismic concept design of buildings［J］.Journal of Building Structures，2008，29（4）：20－25.

［3] 李宏男，肖诗云，霍林生.汶川地震震害调查与启示［J］.建筑结构学报，2008，29（4）：10－19.LI Hongnan，XIAO Shiyun，HUO Linsheng.Damage investigation and analysis of engineering structures in the Wenchuan earthquake［J］.Journal of Building Structures，2008，29（4）：10－19.

［4] 管民生，杜宏彪.现浇楼板参与工作后框架结构的pushover分析研究［J］.地震工程与工程振动，2005，25（5）：117－123.GUAN Minsheng，DU Hongbiao.Pushover analysis of effect of casting slab on RC frame structure［J］.Earthquake Engineering and Engineering Vibration，2005，25（5）：117－123.

［5] 马千里，叶列平，陆新征，等.现浇楼板对框架结构柱梁强度比的影响研究［C］∥汶川地震建筑震害调查与灾后重建分析报告，北京：中国建筑工业出版社，2008：263－271.

［6] 蒋永生，陈忠范.整浇楼板框架节点自控实验研究［J］.东南大学学报，1994，24（3）：59－64.JIANG Yongsheng，CHEN Zhongfan.Experimental research on self－control of frame joint with casting Slab［J］.Journal of Southeast University，1994，24（3）：59－64.

［7] 蒋永生，陈忠范，周绪平，等.整浇梁板的框架节点抗震研究［J］.建筑结构学报，1994，15（6）：11－16.JIANG Yongsheng，CHEN Zhongfan，ZHOU Xuping，et al.Aseismic research on RC frame joint of monolithically casted slab［J］.Journal of Building Structures，1994，15（6）：11－16.

［8] LéGERON F，PAULTRE P.Uniaxial confinement model for normal and high－strength concrete columns［J］.Struct Eng，2003，129（2）：241－252.

［9] GB 50010—2002钢筋混凝土设计规范［S］.