基于逆高斯分布的复合高斯海杂波建模研究

闫 亮 孙培林 易 磊 韩 宁 汤 俊

①(北京林业大学工学院 北京 100083)

②(清华大学电子工程系 北京 100084)

③(北京林业大学理学院 北京 100083)

1 引言

随着雷达分辨率的提高，杂波的统计特性偏离了高斯分布，为此人们提出了诸如对数正态分布，Weibull分布，K分布，t分布等非高斯分布模型[1,2]。然而，复合高斯分布模型可以作为一种更为广义的非高斯分布模型，其合理性已通过实测杂波数据的统计分析得到验证。在复合高斯分布模型中，其纹理分量决定了杂波的非高斯特性，其中K分布假定其服从Gamma分布而得到了广泛的应用。然而，K分布模型存在以下两个缺点：(1)其概率密度函数曲线在峰值后段不能与海杂波幅度的统计直方图精确地吻合；(2)服从Gamma分布随机序列的生成过程涉及非线性变换，不能保证其具有任意功率谱密度。在文献[3]中，Ollila采用服从逆高斯分布的纹理分量建立了一种仅含形状参数的复合高斯(IG-CG)分布模型，相对于K分布模型具有较好的拟合精度。但对于偏态系数较大的非高斯杂波，K分布模型更能准确地与实际杂波数据相吻合。因此，K分布模型和单参数的IG-CG分布模型都具有一定的局限性。

本文主要在以下两方面进行了研究：(1)采用包含形状参数和均值参数的逆高斯分布调制复高斯过程建立了一种双参数IG-CG分布模型，并推导了其统计特性；(2)利用IPIX雷达杂波数据研究了双参数IG-CG分布模型、单参数IG-CG分布模型和K分布模型在不同非高斯程度下的拟合效果，结果表明本文提出的双参数 IG-CG分布模型相对于其它两种分布模型不仅具有更高的拟合精度而且具有更广泛的适用范围。

2 IG-CG分布海杂波模型

2.1 复合高斯分布模型

复合高斯分布模型是由复高斯随机矢量与非负尺度随机变量混合形成[3－5]，其表达形式为：

其中，X称为散斑分量，服从复高斯分布，即X～CNn(0,S),S为复高斯随机矢量的协方差矩阵；τ为纹理分量，假定其概率密度函数为fτ(τ)，其典型分布有Gamma分布，逆Gamma分布等[4]。

记Z=[z1z2… zn]T为n维复合高斯随机矢量，即Z～ CGn(0,S,fτ(τ))，则其联合概率密度分布函数为：

其中，Cn为归一化常数。

由复合高斯分布模型可知，对任意随机变量zi,i=1,2,…,n都对应于同一分布的纹理分量。假设，令R=，则R的概率密度函数为：

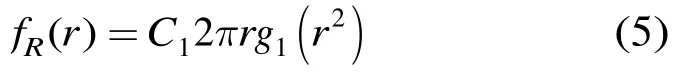
由式(5)得，海杂波幅度的概率密度函数为：

根据复合高斯分布模型，相关学者提出了Weibull分布，t分布，K分布等模型，其中K分布模型在海杂波建模过程中得到广泛的应用[2,6]。在K分布模型中，其纹理分量服从 Gamma分布，即，则：

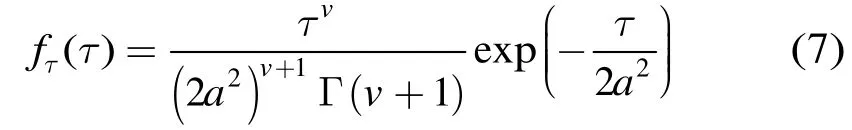
将式(3)，式(4)及式(7)代入式(6)，得K分布的概率密度函数为：

其中，Γ(·)为 Gamma函数；Kv(·)为第 2类修正Bessel函数；a为尺度参数，v为形状参数。

2.2 IG-CG分布模型建立

由于复合高斯分布模型中的纹理分量决定了杂波的非高斯特性，而逆高斯分布相对于Gamma分布具有更好的“高尖峰，长拖尾”特征，因此本文采用服从逆高斯分布的纹理分量建立复合高斯分布模型，即 τ ～ IG(μ,λ)，其概率密度函数为：

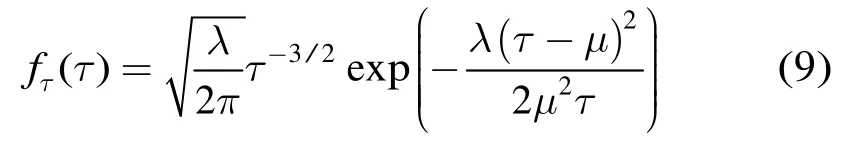
其中，λ为形状参数；μ为均值参数。

逆高斯分布描述的是布朗运动中粒子首次到达固定距离所需的时间，其具有以下性质：

性质1 若 X ～ IG(μ,λ)，则 kX ～IG(k μ,kλ)。

性质2 若 Xi～ IG(μ,λ)，则Xi～IG(n μ,n2λ)。

根据以上两个性质可知，服从逆高斯分布的随机序列经线性变换后仍服从逆高斯分布。该特性使得在生成相关逆高斯分布序列时，只需利用线性滤波器即可使其具有任意功率谱密度函数，进而简化了相关IG-CG分布序列的生成过程。

将式(9)代入式(3)可得：

由式(5)，式(6)，式(10)得到 IG-CG 分布的概率密度函数为：

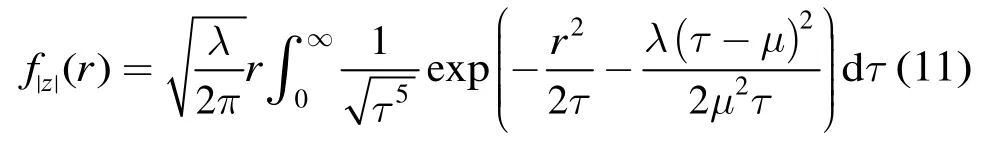
由于式(11)中包含有积分项，因此利用贝塞尔函数对其进行整理后得到 IG-CG分布的概率密度函数为：

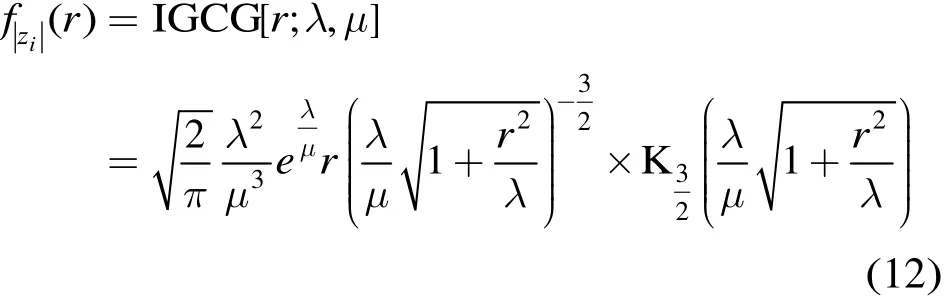
其中，K3/2(·)为第2类修正贝塞尔函数。

根据式(12)可得IG-CG分布的期望和方差分别为：

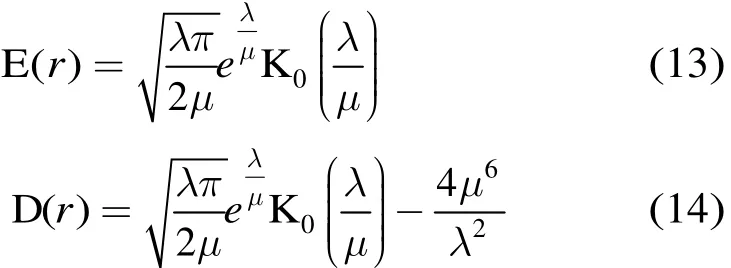
在双参数IG-CG分布模型中，令μ=1，则可得到单参数IG-CG分布模型：

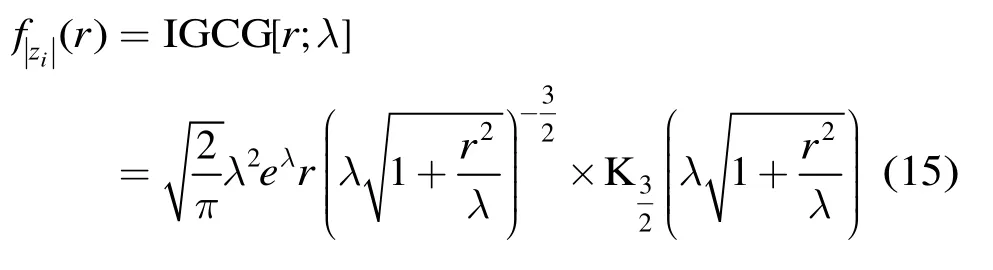
3 IG-CG分布海杂波模型的验证分析

本文选用了400组McMaster大学的IPIX型雷达于1998年在Grimsby采集的海杂波数据，每组数据都为一复数向量(向量大小约为60000)，代表雷达在同一距离单元不同时刻得到的回波数据[7]。针对每组杂波数据，分别利用K分布模型、单参数IG-CG分布模型和双参数IG-CG分布模型进行了拟合，其参数通过最小二乘法估计得到[8,9]。同时，利用残差平方和(Residual Sum of Squares,RSS)衡量每个模型的拟合精度，其定义见式(16)。

其中，ys和分别为拟合模型和实际观测数据在各点的取值。

在该文中给出了其中4组数据的拟合结果，其相关参数及RSS见表1，对应的拟合效果如图1所示。

表1 仿真参数及拟合指标Tab.1 Parameters of models and RSS

图1结果初步表明双参数IG-CG分布模型始终能够更加准确地与实测杂波数据的统计直方图相吻合，而单参数IG-CG分布模型和K分布模型仅在一定的杂波特性下才具有较好的拟合效果。为了进一步研究以上3种模型在不同杂波特性下的拟合精度，本文采用峰态系数和偏态系数描述杂波数据的非高斯特性，其统计表达式见式(17)和式(18)。

其中，mn是n阶样本中心距，xi为第i个样本值，为样本平均值。

根据式(16)，式(17)可得到400组峰态系数和偏态系数，按其取值大小等间隔地分为40组，并对间隔内数据对应的3种模型的RSS进行均值处理。图2，图3分别为3种模型的RSS与峰态系数和偏态系数的关系曲线。

图2结果表明，相对于单参数IG-CG分布模型和K分布模型，双参数IG-CG分布模型具有更小的RSS，其拟合效果最好。图3结果表明，当偏态系数小于5.2时，单参数IG-CG分布模型较K分布模型具有较好的拟合效果；而当偏态系数大于 5.8时，K分布模型具有较高的拟合精度。然而，双参数 IG-CG分布模型在偏态系数范围内始终具有更高的拟合精度。因此，本文建立的双参数IG-CG分布模型较其它两种分布模型具有明显的优势。

4 结束语

本文利用逆高斯分布建立了一种双参数IG-CG分布模型，经IPIX雷达杂波数据统计分析表明相对于单参数IG-CG分布模型和K分布模型，该模型对不同非高斯特性的杂波数据都能准确地与其统计直方图相吻合。然而，针对IG-CG分布海杂波模型，仍有部分研究内容需要开展，其中该模型的相关性研究对基于零记忆非线性变换法(ZMNL)的海杂波仿真实现有着重要的意义[10,11]。

[1]Skolnik M I.Radar Handboo-3Rd[M].New York: McGraw-Hill,2008: 720-752.

[2]Marier L J.Correlated K-distributed clutter generation for radar detection and track[J].IEEE Transactions on Aerospace and Electronic Systems,1995,31(2): 568-580.

[3]Ollila E,Tyler D E,Koivunen V,et al..Compound gaussian clutter modeling with an inverse gaussian texture distribution[J].IEEE Signal Processing Letters,2012,19(12):876-879.

[4]Raj R G and Bovik A C.The multilinear compound gaussian distribution[C].2012 IEEE International Conference on Acoustics,Speech and Signal Processing(ICASSP),Kyoto,Japan,2012: 3849-3852.

[5]Stinco P,Greco M,and Gini F.Adaptive detection in compound-gaussian clutter with inverse-gamma texture[C].2011 IEEE CIE International Conference on Radar,Chendu,China,2011: 434-437.

[6]王颖,毛二可,寒月秋,等.相关K分布杂波的建模与仿真[J].信号处理,1997,13(2): 141-146.Wang Ying,Mao Er-ke,Han Yue-qiu,et al..Modeling and simulation of correlated K-distributed clutter[J].Signal Processing,1997,13(2): 141-146.

[7]McMaster University. IPIX radar database[OL].http://soma.ece.mcmaster.ca/ipix/grimsby/index.html.1998.

[8]姜斌,和湘,任双桥,等.广义复合杂波模型参数估计方法[J].电路与系统学报,2009,14(1): 87-92.Jiang Bin,He Xiang,Ren Shuang-qiao,et al..Parameter estimation method for generalized compound clutter model[J].Journal of Circuits and Systems,2009,14(1): 87-92.

[9]任双桥,刘永祥,黎湘,等.广义K分布杂波模型参数估计[J].电子学报,2006,34(12): 2278-2281.Ren Shuang-qiao,Liu Yong-xiang,Li Xiang,et al..Parameters estimation for generalized K-distributed clutter model[J].Acta Electronica Sinica,2006，34(12): 2278-2281.

[10]Watts S.A new method for the simulation of coherent sea clutter[C].IEEE Radar Conference (RADAR),Kansas City,USA,2011: 052-057.

[11]陈金明.基于ZMNL的相关广义K分布宽带雷达杂波仿真[J].电子科技,2010,23(10): 72-75.Chen Jin-ming.Simulation of correlated generalized K-distribution wide band radar clutter based on ZMNL[J].Electronic Science & Technology,2010,23(10): 72-75.