基于FPGA的杂波模拟系统的设计与实现

刘冰徐飞

(西安电子工程研究所 西安 710100)

0 引言

雷达的环境杂波是雷达工作环境中的重要组成部分，无论是什么体制的雷达都会受到各种杂波的干扰，从杂波中发现目标回波，并从中提取目标信息是雷达信号处理的基本任务之一，因此研究并仿真各种类型的杂波就成了雷达系统仿真的一个重要部分。在实验室模拟出逼真的杂波环境有助于雷达杂波滤波器的设计及优化，提高杂波抑制能力，从而用最小的代价，达到预期的性能指标。

任何杂波特性都可以用幅度分布特性和频率分布特性来描述，因此杂波建模仿真［1－2］就是基于某种方法产生出既要满足一定幅度又要满足一定相关特性的随机序列。目前经典的相关杂波序列产生的办法主要有零记忆非线性法(ZMNL)，此方法实现简单，运算量小比较适合工程实现。本文基于FPGA硬件平台结合ZMNL方法对最常见的地杂波和海杂波进行建模仿真，给出结果并进行分析。

1 杂波模型

1.1 高斯相关瑞利分布地杂波模型

瑞利分布杂波概率密度函数为:

式中，σ为瑞利分布的参数。

杂波功率谱为:

1.2 高斯相关K分布海杂波模型

K分布概率密度函数如下:

式中，Γ(·)为Gamma函数;kv(·)为第二类修正Bassel函数;v是形状参数;a是尺度参数。杂波平均功率σ2、v和a之间的关系可表示为对于大多数雷达来说，形状参数v的取值范围为0.1＜v＜∞，v→0.1杂波有长的拖尾，v→∞ 杂波的分布接近瑞利分布。对于高分辨低擦地角的海杂波v的值在0.1到3之间。杂波功率谱为高斯谱。

2 基于FPGA的杂波模拟系统设计

2.1 系统设计

2.1.1 随机噪声的FPGA实现［3－4］

首先我们介绍一下基于FPGA的随机噪声生成的方法，这个是杂波模拟的前提。m序列是由带线性反馈的移位寄存器产生的序列，并且具有最长周期。一般情况下，n级线性反馈移位寄存器如图1所示。

图1 n级线性反馈移位寄存器

图1中Ci(i=0，1，…，n)表示反馈线的连接状态:Ci=1表示连接线通，第n－i级输出加入反馈中;Ci=0表示连接线断开，第n－i级输出未参加反馈。

因此，一般形式的线性反馈逻辑表达式为:

本文基于FPGA，使用移位寄存器，异或门等电路来产生所要求的M序列，采用Verilog进行编程实现，程序中设计了20位的移位寄存器产生M序列码，其周期为220－1=1048575。

2.1.2 基于FPGA的瑞利杂波建模

根据ZMNL方法实现杂波模拟的原理，生成高斯分布的随机序列是杂波模拟的第一步，上面已经介绍了如何基于FPGA产生随机信号，进一步根据随机信号处理理论我们就可以产生高斯随机序列，具体实现过程如图2所示，其实质是一组随机序列经过一个窄带滤波器，这个滤波器H(ω)使得通过它的随机序列具有了相关性，在这里为了节省资源我们采用频域法实现整个过程。

图2 相关高斯序列FPGA实现框图

另外，由于FPGA实现浮点算法能力有限，H(ω)可通过MATLAB产生并转化成相应的格式导入fir滤波器。为使得H(ω)物理可实现，在仿真过程中选择了服从(－π，π)均匀分布的φ(ω)来构造系统响应。

图3给出了产生瑞利分布杂波的FPGA实现过程，将两组随机序列xi，xq同时通过同一个滤波器，产生的两组高斯相关随机序列yi，yq分别作为杂波信号的实部和虚部。这样产生的杂波信号幅度服从瑞利分布，同时在时间上具有了相关性。

图3 相关瑞利分布杂波FPGA实现框图

2.1.3 基于FPGA的K杂波建模［5］

K杂波可以在时间和空间上更好的模拟实际海杂波，是目前被广泛应用的杂波模型。根据ZMNL法产生K杂波的关键就是找出非线性变化前后相关系数某种程度上的关系，即建立相关高斯分布随机序列与相关K分布随机序列的相关函数间的关系，文献［6］中推导了这种关系表达式:

F1(·)为超高斯分布。

由于sij与rij和qij有关，因此有无限种组合满足这个方程。为了计算sij一般将所有的相关系数都设成相同的值，即rij=qij，这时sij与rij非线性最小，与v关系不大，即经过ZMNL变换后相关高斯分布随机序列的频谱与相关K分布随机序列的频谱之间的非线性最小。由于确定这种非线性关系需要经验迭代法，算法复杂，本文借助于MATLAB完成，将获得的系数存入FPGA中备用，具体过程如下:

a.按照给定的功率谱密度函数得到序列Sn，其中 n=1，2，…N;

b.对序列Sn，进行IFFT变换，获得所求的随机序列的自相关函数序列sij;

c.查sij与rij之间的关系曲线，求得rn;

d.对序列rn进行FFT变换，得到随机序列X及Y的功率谱密度序列，进而得到线性滤波器系数，并将系数转化成FPGA中所需的格式存入FPGA中使用。

图4给出了基于FPGA实现K杂波模拟的流程图，首先产生四组相互独立的高斯噪声，分别将前两组和后两组通过滤波器H1(f)和H2(f)，然后经过图示的非线性变换就获得了K分布杂波，在这里同样选择了服从(－π，π)均匀分布 φ(ω)构造合适的相角。

图4 相关K分布杂波FPGA实现框图

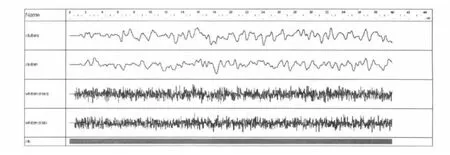
图5 FPGA仿真结果图

2.2 仿真结果及分析

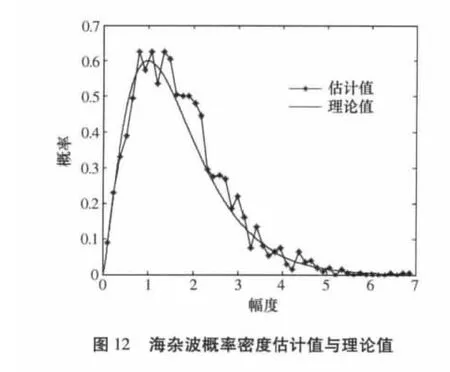
首先产生高斯白噪声如图5中writeclutteri和writeclutterq所示，然后再产生具有相关特性的杂波序列，分别用clutteri和clutterq表示它的实部和虚部，由于在FPGA中无法分析其幅度分布和频谱特性，在此我们将数据导入MATLAB中进行分析，图6和图7给出了writeclutteri的直方图及功率谱，从图中可以看出其为服从正态分布的白噪声。图8、图9、图10分别给出了服从相关瑞利分布的地杂波的幅度和功率谱特性，图11、图12、图13分别给出了服从相关K分布的海杂波的幅度和功率谱特性，从中可以看出，模拟杂波的概率密度分布特性与相应的理论值吻合的很好，而功率谱也符合我们预先的设计。

3 结论

本文基于FPGA建立了相关瑞利分布的地杂波模型，相关K分布的海杂波模型，实现了这两种典型杂波模型的实时模拟。结果表明，用该种方法产生的杂波能够很好地满足所要求的功率谱特性和幅度特性，说明了该方法的有效性，并且该系统可以通过灵活的改变参数适应不同系统的要求，为实验室进行雷达信号处理调试提供了逼真的杂波环境，减少了研制成本，缩短了调试时间。

［1］Irina Antipov.Statistical Analysis of Northern AustralianCoastline Sea Clutter Data［R］.Edinburgh，South Astralia:DSTO Electronics and Surveillance Research Laboratory，2001.

［2］Simon Haykin，Stanislav Kesler，Briancurrie.An experimental classification of radar clutter［J］.Proceedings of the IEEE.1979，67(2):332－333.

［3］D Liu，D Cmunson.Generation of a random sequence giving a jointly specified marginal distribution and autocovariance［J］.IEEE Trans.on ASSP，1982，ASSP－30:973－983.

［4］李欢.伪随机序列的FPGA设计与实现［J］.科技信息，2011，(17):508.

［5］刘江波等.基于ZMNL的K分布海杂波仿真［J］.电子信息对抗技术，2011，26(3):52－54.

［6］WATTS S.Radar detection prediction in sea clutter usingthe compound K-distributionModel［J］.IEEEProcessing Pt F，1985，132(6):613－620.

［7］James L M.Correlated K-distributed clutter generation for radar detection and track［J］.IEEE Trans.on AES，1995，31(2):568－580.