基于改进非参量法的现代空战威胁评估研究

孙永芹 世文荣 彭海军 纪金耀

(1.中国人民解放军91206部队 青岛 266108;2.海军航空工程学院青岛校区 青岛 266041;3.海军潜艇学院 青岛 266071)

0 引言

近年来，威胁评估研究越来越受到关注［1～6］，目前常用的威胁评估算法有参量法和非参量法。其中，非参量法模型简单、易用，便于机载火控计算机实时计算，其实质是解决一个多属性决策问题。通常都要考虑属性权重，属性权重的合理性直接影响着多属性决策排序的准确性。确定属性权重的方法可分为主观赋权法、客观赋权法两大类。主观赋权法如专家调查法、二项系数法、AHP法等，是根据决策者主观偏好信息间接或决策者根据经验直接给出属性权重。客观赋权法如主成分分析法、多目标优化方法等，是根据决策矩阵信息，通过一定的数学模型计算出权重系数。两种方法各有优缺点，近年来，有人进行了融合和改进，取得了一些成绩［7～9］。但这些方法所用的威胁评估模型大多参考了近距空战的威胁评估模型，并以态势透明与实力对等为前提，已经不适于超视距空战的威胁评估。文献［10］提出了一种超视距空战威胁评估非参量法模型，但是该方法所构造的优势函数等模型也存在不足。本文针对现有威胁评估非参量模型的不足，结合对现代空战过程和影响参数的分析，提出一种改进的威胁评估非参量方法。

1 现代空战威胁评估非参量法研究

在现代空战中，敌方目标威胁程度的大小是由多种因素决定的，在威胁评估时必须综合考虑。本文结合现代空战实际，综合考虑双方战机(包括其武器)性能，从整个体系做出分析，选取来自空战态势、空战效能、对双方做出威胁行为的事件、目标战役价值为主要影响威胁评估的因素，建立威胁评估的非参量法模型。如框图1所示。

图1 威胁评估框图

1.1 空战效能优势模型

空战能力指数C，本文取参考文献［11］中的定义。该空战能力计算公式已经很全面的反映了各种类型飞机的作战能力。但是，在目前的空战威胁评估研究中，大多仅考虑敌机的空战能力，而没有与我机进行对比分析，这样做是不全面的，有可能对作战效果造成不利的影响。例如，把极具威胁的目标分配给了我方某架战机，而我方这架战机的实际武器装备却并不具备毁伤该目标的能力。为了避免上述情况的发生，更符合超视距空战实际，将目标机与我机的空战能力进行对比分析，构造如下空战效能优势:

首先，将空战能力指数进行归一化处理，这里取空战能力指数的相对值:

式中，i是第i架飞机。

接下来，构造空战效能优势函数:

式中，TCA、TCT分别为归一化后的战斗机与目标机的空战能力指数。

1.2 空战态势优势模型

1.2.1 距离优势函数建模

目前公开发表的威胁评估的文章中，构造距离优势函数时考虑的威胁因素并不相同。本文采用文献［10］的思路，在现代空战中，距离对优势函数的影响主要反映在雷达发现概率和导弹的杀伤概率上;并将战斗机和目标机之间的距离D分为雷达最大搜索距离DRmax、导弹最大攻击距离DMmax、导弹不可逃逸区最大距离DMkmax、导弹不可逃逸区最小距离DMkmin。但文献［10］认为，D ≥ DRmax时，优势函数等于零是不符合实际的。随着现代空战协同作战能力的提高，在D≥DRmax时，虽然不能依靠自身探测设备发射武器，但可以借助其他平台传送的目标信息，装订目标参数，发射远程攻击武器。所以，D≥DRmax时，不可简单的认为等于零。故而，构造如下距离优势函数:

1.2.2 角度优势函数建模

目前公开发表的威胁评估的文章中，多数采用文献［7］、［9］中的研究思路，所建模型在视距内有效。在超视距空战中，进入角对优势函数的影响主要体现在对导弹杀伤概率的影响上。双方迎头作战和尾追条件下，进入角的优势是不同的。故而构造进入角优势函数:

式中，φ是目标方位角，q是目标进入角。0≤|q|≤180°，0 ≤| φ |≤180°，且 |q|+| θ|=180°。

方位角对优势函数的影响主要反映在雷达发现概率和导弹的杀伤概率上，当目标由雷达搜索区以外的区域，逐渐进入雷达搜索区、导弹攻击区、不可逃避区时，其方位角优势函数值逐渐增大。但在D≥DRmax时，文献［10］简单认为方位角优势函数为零，这并不符合实际情况。在该区域，尽管方位角优势函数值相对较小，但是不能简单的等于零。故而给出如下方位角优势函数:

式中，φ是目标方位角;φRmax为雷达最大搜索方位角;φMmax为空空导弹最大离轴发射角;φMkmax为不可逃逸区圆锥角。

构造整机的角度优势为方位角优势和进入角优势的乘积，如下式所示:

式中，γ1，γ2为权重系数，用以调整二者在乘积中的比例。

1.2.3 能量优势函数建模

在现代空战中，当载机高度变化时，导弹射程等参数也随之改变［12］。所以，传统评估算法没有考虑战机高度对优势函数的影响是不合理的。另一方面，载机速度对导弹射程也是有影响的，而且战机速度较大时，能够在空战中尽快机动到最佳空战位置，从而对敌方具有空战优势。因此，结合战机高度和速度构造能量优势函数。定义战机单位能量为E=H+v2/2g，则战机能量优势数为:

式中，E表示战机能量;ET表示目标机能量;v表示战机速度;g表示当地重力加速度。

1.2.4 态势优势函数建模

综合角度优势、距离优势、能量优势，即可得到态势优势。由于三者之间并不完全独立，因此处理为乘法关系。

式中，β1、β2、β3分别为战斗机相对于目标机的角度优势、距离优势、能量优势的权值。

1.3 空战事件优势模型

空战实体在作战过程中会不断出现加(减)速、拐弯、爬升、辐射源开(关)机、导弹符合发射条件等属性变化行为，这些行为都可能对对方空战实体产生威胁，这些产生威胁的行为即事件。事件优势涉及面广，尤其是复合事件，需要经专家系统确定其优势，本文简单选取以下几个具备代表性的相关事件，并定义如下事件优势TI。

a.实体雷达辐射:未辐射时，TI取0;战斗机对目标机扫描时，TI取0.5;战斗机对目标机多目标跟踪时，TI取0.8;战斗机对目标机连续跟踪时，TI取1。

b.实体导弹发射:战斗机对目标机发射导弹时，TI取1。

1.4 目标战役价值对威胁评估的影响

任何空中战斗都是在双方各自的任务背景下进行的。执行的任务不同，相应地就会影响对目标战役价值的评价。目标的战役价值一般由作战指挥系统确定，也可以根据目标的对地攻击能力或者特种作战能力(预警、电子干扰等)确定。目标的对地攻击能力可以由对地攻击能力指数评价。对地攻击能力指数L的计算公式为［11］:

式中Γ为当量航程，Θ为当量载弹量，ε1为电子对抗能力系数。

1.5 总体优势函数的构造

综上所述，战斗机对目标机的总体优势函数直接线性加权法构造为:

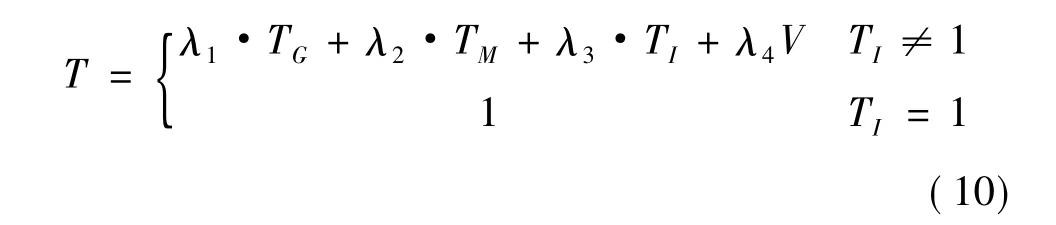
式中，λ1、λ2、λ3、λ4分别是战斗机相对于目标机的态势优势、效能优势、事件优势、目标战役价值的权重。合理地确定权重非常重要，它对排序结果将产生很大影响。为克服主观因素影响，客观反映各因素之间的权重比例，本文采用熵权法［7］求权重。计算步骤如下:

Step 1: 构造决策矩阵A=(aij)n×m。其中n为空战目标(方案)个数，m为威胁指标(属性)个数，aij为第i个目标在第j个威胁指标下的属性值。用式(1)～式(10)将决策矩阵A经过规范化处理后，得到规范化矩阵 R=(rij)n×m。

2 仿真验证与分析

针对目标进入角、方位角、双机相对距离、高度、效能变化对总体态势优势指数的影响进行了仿真，仿真数据为:φRmax=65°，φMmax=35°，φMkmax=20°;DRmax=140km，DMmax=80km，DMkmax=60km，DMkmin=40km。图2～6分别为空空作战空战优势随不同参数的变化图。

图2 中，虚曲线:q=0°;实曲线:q=120°时，空战优势随方位角变化情况。由图可以看出，在不同的进入角下，相同的方位角对应的空战优势不一样。

图3 中，实曲线:φ =0°;虚曲线:φ =60°时;空战优势随进入角变化情况。由图可以看出，在不同的方位角下，相同的进入角对应的空战优势也不一样。

图4中曲线是 φ=0°，q=180°时，空战优势随距离变化情况。该图反映了目标机在导弹不可逃逸区内时空战优势最大。

图5中曲线是目标机高度=1000m时，空战优势随战斗机高度变化情况。由图可以看出，空战优势随战斗机的高度的增大而增大。

图6中曲线是空战优势随空战效能变化情况。由图可看出，空战优势随战斗机效能优势的增大而增大。

图5 空战优势随战斗机高度变化图

针对事件、目标战役价值作为威胁评估的因素进行仿真，假设现代空战中，红机i是F-16C，8架三种类型的蓝机，分别是 F-16C、F-15E、F-5E三种类型，其空战能力指数C为:16.8、19.8、8.2;且都在红机i火控雷达的跟踪范围内。8架蓝机的相关参数、目标属性值及战役价值如表1所示。考虑空空作战，当不考虑事件优势时，得到红机i对8架蓝机的总体优势函数值，如表2所示。考虑事件优势作为威胁评估因素时，仿真所得红机i对8架蓝机的总体优势函数值如表3所示。设执行要地防空任务，仿真所得红机i对8架蓝机的总体优势函数值如表4所示。表2、表3、表4中T代表总体优势函数值，Y代表优势排序。

图6 空战优势随空战效能变化图

表1 8架蓝机的相关参数、目标属性值及战役价值表

表2 红机i对8架蓝机的总体优势函数值表

表3 事件优势作为威胁评估因素时，红机i对8架蓝机的总体优势函数值表

表4 执行要地防空任务时，红机i对8架蓝机的总体优势函数值表

由表2得8架蓝机对红机i最终的威胁排序为(由大到小):(5，2，6，1，3，4，8，7)。表 3 得到的威胁排序是:(5，2，6，1，4，3，8，7)。比较两个排序结果可以看出，事件优势对威胁排序有影响。如蓝机3优势值小于蓝机4，但蓝机3的事件优势大于蓝机4，故而考虑事件优势时，蓝机3的威胁下降，影响了威胁排序，由第五位降低到第六位。由计算结果可见，事件优势影响了目标威胁排序结果。

由表4得8架蓝机对红机i最终的威胁排序为(由大到小):(4，3，5，8，6，7，2，1)。表 3 得到的空空作战时威胁排序是:(5，2，6，1，4，3，8，7)。比较两个排序结果可以看出，目标战役价值对威胁排序有影响。如蓝机1的态势、效能和事件优势之值较小，但目标战役价值比较大，当执行如要地防空的任务时，目标战役价值就影响目标的威胁排序，由第四位降低到第八位。由计算结果可见，执行的任务不同，相应地就会影响对目标战役价值的评价，继而影响威胁排序结果。

综上所述，由图2～6可知，本文对效能、距离、角度、能量优势函数模型的优化、改进更符合超视距空战的实际。由表2～4可知，将事件、目标战役价值作为威胁评估因素是符合空战实际的，所以，本文所建模型合理、有效。

3 结束语

综上所述，本文综合考虑态势优势、效能优势、事件优势、目标战役价值，研究了现代空战威胁评估方法，建立了改进非参量法的威胁评估模型，优化了态势优势、效能优势威胁因素，增加了事件优势、目标战役价值威胁评估因素，并采用熵权法求权重，客观反映各因素之间的权重比例，从而更符合实际空战实际。最后进行了仿真分析，仿真结果表明所建立的模型合理、可行。

［1］CHEN Jun，YU Guan-hua，GAO Xiao-guang.Cooperative threat assessment of multi-aircraftsbased on synthetic fuzzy cognitive map［J］.J.Shanghai Jiaotong Univ.(Sci.)，2012，17(2):228－232.

［2］黄洁，李弼程，赵拥军.基于Choquet模糊积分的目标威胁评估方法［J］.信息工程大学学报，2012，13(1):18－21.

［3］王改革，郭立红，段红等.基于 Elman-Ada-Boost强预测器的目标威胁评估模型及算法［J］.电子学报，2012，40(5):901－906.

［4］蔡佳，胡杰，黄长强.协调优势粗糙集方法及其在UCAV目标威胁估计中的应用［J］.系统工程理论与实践，2012，32(6):1377－1384.

［5］陈华，张可，曹建蜀.基于PSO-BP算法的目标威胁评估［J］.计算机应用研究，2012，29(3):900－901，932.

［6］韩占朋，王玉惠，姜长生等.基于马尔可夫链的新型威胁评估预测方法［J］.吉林大学学报(信息科学版)，2012，30(2):151－156.

［7］谷向东，童中翔，郭辉等.IAHP和熵权相结合的TOPSIS法的空战目标威胁评估［J］.火力与指挥控制，2012，37(1):69－72.

［8］Gong Y.B.，Chen S.F.，Multi-attribute decision-making based on subjective and objective integrated eigenvector method［J］.Journal of Southeast University(English Edition)，2007，23(1):144－147.

［9］谷向东，童中翔，柴世杰等.基于IAHP和离差最大化TOPSIS法目标威胁评估［J］.空军工程大学学报(自然科学版)，2011，12(2):27－31.

［10］高永，向锦武.一种新的超视距空战威胁估计非参量法模型［J］.系统仿真学报，2006，18(9):2570－2573.

［11］朱宝鎏，朱荣昌，熊笑非.作战飞机效能评估［M］.北京:航空工业出版社，2006.

［12］马伟江，姚佩阳，冯煊，等.基于多级模糊综合评判法的态势评估方法研究［J］.电光与控制，2011，18(62):21－25.