雷达目标检测概率简化算法及应用分析

2013-09-30郑全普张凤伟霍烁烁

火控雷达技术 2013年3期

郑全普张凤伟霍烁烁

(中国洛阳电子装备试验中心洛阳 471003)

0 引言

雷达试验是电子装备试验的重要项目。在雷达检飞试验中，检测雷达威力即雷达作用距离是一项重要内容，分析计算的依据是统一的雷达方程和目标的平均雷达散射截面积(RCS)。雷达威力的检测都是假定恒定的雷达散射截面积，通过这种方法，可基本实现对雷达性能的检测和评估。但在此过程中，由于目标的散射截面积受目标起伏的影响而存在统计特性，且受目标速度、姿态和雷达频率的影响表现出不同的统计特性，在进行雷达检飞时，需要把不同类型的起伏目标等效到非起伏目标上。

关于雷达目标的起伏模型，最典型的是Swerling(施威林)I-IV模型，非起伏目标被称为Swerling0或SwerlingV模型。目标的起伏降低了检测概率，等效地降低了接收端的信噪比。而目标起伏造成的信噪比损失，通过合理的建模，可以定量分析出来。在雷达检飞实际应用中，所采用的雷达方程就是假定目标是非起伏的，目标雷达散射截面积是平均散射截面积，在一定检测概率条件下的，使起伏目标等效为非起伏目标，进而求出雷达的威力等。针对雷达在非起伏目标条件下的发现概率、虚警概率和信噪比之间的关系，很多文献都有描述。本文主要针对Marcum提出的非起伏目标模型，给出了一种简化算法，并对简化后的误差进行了仿真分析，并通过合理的建模，使起伏目标转换为非起伏目标，并对转换后的应用进行了简要分析，这为靶场试验的提供了理论支撑。

1 起伏目标的等效

1.1 起伏目标模型

关于起伏目标模型，文献［1］、［2］对 Swerling起伏模型进行了系统的阐述，同时还提出了χ2分布、对数正态分布、莱斯分布等模型;文献［3］、［4］提出采用自由度为2m的χ2分布对多种目标起伏模型进行近似，Swerling模型为m=1或2时χ2分布的特殊形式。在这些模型中，Swerling模型研究的最为广泛和典型。其中，SwerlingI和SwerlingII型对应于多个反射体，没有主反射体，且各个散射体单元相互独立，SwerlingI型对应于目标的慢起伏，而SwerlingII型对应于目标快起伏;SwerlingIII和SwerlingIV型对应于存在一个主反射体和多个副反射体，SwerlingIII型对应于目标的慢起伏，而SwerlingIV型对应于目标快起伏。第一、二类模型是用于复杂目标是由大量RCS近似相等的散射体组成的情况，虽然理论上要求独立散射体的数量很大，实际上只需四、五个即可，如飞机就属于这一类;第三、四种模型适用于目标是有一个RCS较大的散射体和许多小散射体组成，或者一个强散射体在方位上有小的变化的情况。

1.2 目标起伏损失及等效

在雷达方程中，若目标在某距离处的回波功率等于接收机最小可检测功率，则定义该距离为雷达最大作用距离。即

式中Pt为峰值发射功率;Gt为发射天线增益;Gr为接收天线增益;λ为波长;σ为目标截面积;k=1.38×10－23为波尔兹曼常数;T0为有效噪声温度，通常取290K;Bn为接收机带宽;Fn为系统噪声系数;Ls为雷达系统损耗;(SNR)1min为检测目标单脉冲条件下，所需的最小信噪比。

式中假设目标的RCS恒定不变，在考虑目标起伏和脉冲积累的情况下，给出雷达方程如下:

式中，(SNR)m为积累m个脉冲时雷达检测目标所需的信噪比;I(m)为积累改善因子。

由式(2)可知，Rmax是(SNR)m的函数。不同的起伏目标相对于非起伏目标而言，具有不同的σ和Lf。在雷达检飞试验中，雷达的威力是雷达在一定发现概率下的作用距离，式(2)保留Rmax、(SNR)m、σ和Lf，其它项是与雷达有关的常量，用因子K代替，雷达方程可以写为［5］

同时，雷达的发现概率和要求的虚警概率与信噪比有关，对于典型的Swerling模型，在虚警概率为1e－6时，单脉冲条件下，信噪比和发现概率之间的关系如图1所示。

图1 Swerling模型起伏目标和非起伏目标检测性能曲线

从图1中可以看出，单脉冲条件下，SwerlingI型和SwerlingII型二者曲线一致，SwerlingIII和SwerlingIV型二者曲线一致;在信噪比较大时，非起伏目标的检测性能高于起伏目标的检测性能，SwerlingIII和SwerlingIV高于SwerlingI型和SwerlingII型;而在信噪比较小时，具有反变的关系。在给定一个发现概率Pd时，起伏目标相对于非起伏目标存在额外的信噪比起伏损耗Lf，可以认为起伏目标等效为非起伏目标所需的额外信噪比，对应的关系如图2所示。

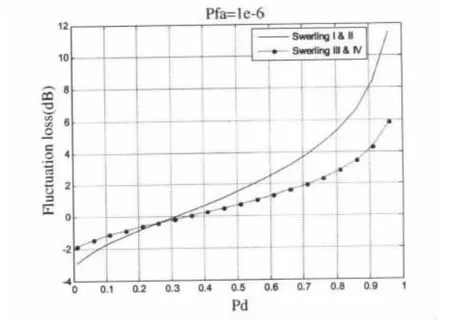
图2 目标起伏损耗相对于检测概率曲线

注意Lf的负值表明是起伏目标获得SNR增益而不是损失。而对于不同虚警概率下的信噪比损失可以制成表存储起来，在实际应用中通过查表可得到对应发现概率下的目标起伏损耗，带入方程(3)可以求得对应起伏目标条件下，雷达的作用距离，完成对雷达威力的检测。

2 检测概率、虚警概率和信噪比之间的关系

检测概率、虚警概率和信噪比之间存在固定的关系，这种关系不因雷达而异，这就为雷达设计提供了有力的参考。

2.1 推导

根据雷达原理可知，对于非起伏的目标而言，其回波信号包络服从广义瑞利，即莱斯(Rice)分布:

如果A/σ2=0(只有噪声)，式(4)变成瑞利(Rayleigh)概率密度函数

式中，A为目标的回波信号幅度(假设雷达信号为连续波);r为目标回波的综合幅度(包括系统噪声等);σ2为系统的噪声信号功率;I0(β)是零阶修正贝塞尔函数，定义为:

虚警概率Pfa是雷达只有噪声出现时，回波信号超过门限VT的概率:

发现概率Pd是回波信号包络超过门限VT的概率:

假设信号的功率为A2/2，则单个脉冲的信噪比为

将式(8)和(9)联立得

即在一定发现概率和虚警概率下所需要的信噪比，为雷达设计者提供了参考。

2.2 简化

由于式(8)的计算过于复杂，当Pfa较小，Pd相对较大，从而门限也较大时，式(8)可以近似为

由于正态分布和补余误差函数之间存在固定关系，针对该近似简化方法，本文给出一种新的简化算法如下。

已知正态分布函数的概率为

补误差函数的概率为

式(14)代入式(13)有如下关系成立

于是，式(10)可简化为:

由于式(16)包含的误差函数是一个非简单函数，为了得到精确的雷达性能概率的估计，必须将数据制成表格或使用计算机计算。然而，存在一些数值的近似和计算技巧，使得雷达的性能估计变得简单。补余误差函数erfc(x)的近似方法和下限表示为［6］

式(17)给出了erfc(x)的上下限，整个距离范围内，下界相当紧密，而上界最好用于x＞0.8的情况。

同时，North曾提出了一个非常准确的近似［7］

对上述方法的仿真分析如图3所示。从图4中可以看出，修改简化和正态简化具有相同的性能，North和理论值曲线基本吻合;简化值和理论值之间存在差距;在相同信噪比条件下，简化的信噪比较小，即在相同概率下，需要更高的信噪比。在实际应用时，应根据具体情况进行，如一般正态分布函数或补误差函数表的形式存在，可直接查表计算。

3 结束语

图3 理论值和简化值的信噪比发现概率曲线

在雷达检飞试验中，雷达最大作用距离和目标起伏模型因素有关，通过合理建模和推导，可以转换为非起伏目标，此时就可以利用经典的雷达方程进行理论分析;同时，雷达的检测端的信噪比和发现概率、虚警概率之间存在稳定关系，这种关系不因雷达而异(实际上随着雷达采用一系列的数据处理技术，这种关系也出现了不稳定的情况，也会因雷达而异)，可以利用这种稳定的关系对雷达进行等效替代推算，即采用已有的试验靶机作为检飞目标，把试验靶机的检飞结果等效推算到对研制要求中规定目标的检测性能上。当等效为非起伏目标时，需要考虑由目标起伏造成的信噪比损耗，通过实测数据与理论分析向比对，进一步验证理论分析的正确性。