地铁车辆轮轨法向接触问题研究＊

孙树磊 丁军君 李 芾 黄运华 周张义

（西南交通大学机械工程学院，610031，成都∥第一作者，博士研究生）

轮轨接触由于对车辆运动状态、轮轨磨耗及滚动接触疲劳有较大影响，一直是国内外研究的热点和重点。自1882年接触理论的创始人Hertz发表了《论弹性固体的接触》论文以来，世界上众多学者在赫兹接触理论的基础上发展了各种轮轨接触模型，取得了较多进展。文献1等假定接触斑每个条带上的法向应力呈半椭圆分布并利用两个接触体之间的穿透量通过迭代获得接触区域［1］。文献2发展了三维弹性体非赫兹滚动接触理论［2］，通过对任意形状的平面接触区离散，并借助于Bossinesq－Cerruti力／位移公式进行数值迭代求得解，又被称为精确理论。文献3等利用有限元方法分析轮轨接触应力分布和接触区域，同时文献4等利用有限元方法研究了轮轨法向接触问题［4］，并利用分析结果对轨头部分进行优化以适应列车高速运行。文献5等发展了一种非迭代的轮轨法向接触快速求解方法，其接触区域为非椭圆［5］。

本文分别基于有限元方法、赫兹接触理论和Kalker精确理论对地铁车辆轮轨法向接触问题进行分析，并比较各种接触模型下的法向接触应力和接触斑形状，为车辆动力学、轮轨磨耗及滚动接触疲劳的进一步研究提供参考。

1 轮轨法向接触模型

1.1 赫兹接触理论

赫兹接触理论在应用时基于弹性半空间假设，且认为接触斑内两物体曲率是常数，物体之间的法向间隙可表达为：

式中：

A、B——相对曲率；

x、y——坐标。

在法向作用力N下，Hertz认为接触斑的形状为椭圆，如图1所示。接触斑半轴长、相对位移量和法向接触应力见式（2）～（5）。

式中：

a、b——分别为椭圆长、短半轴；

m、n、r——赫兹接触参数；

v——泊松比；

E——弹性模量；

δ0——两个固体间相对位移量；

Pz——法向接触应力。

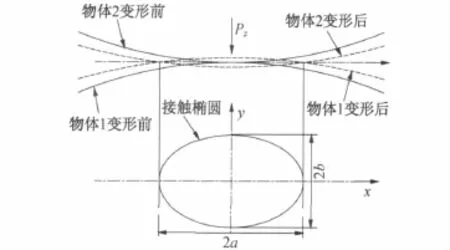
图1 赫兹接触示意图

1.2 Kalker三维弹性体非赫兹滚动接触理论

Kalker从经典弹性力学虚应力功的概念，得到滚动接触问题的余虚功原理，将可能接触区离散成若干个小单元，如图2所示。借助于Bossinesq－Cerruti力／位移公式，使接触问题求解转换为数学规划问题的解［2－6］，见式（6），并编制了精确理论程序CONTACT。

式中：

i，j＝1，2，3——分别为图2中坐标轴x1，x2和x3方向；

τ＝1，2——分别为图2中坐标轴x1和x2方向；

x1，x2和x3——分别表示局部接触坐标系的纵向、横向和法向；

I，J——矩形单元的编号；

C——余能；

AIiJj——力和位移的影响系数，其意义是作用于A处沿j方向单位力引起接触面上另一点B处沿i方向的位移；

PIi和PJj——分别为接触单元I和J处的作用力密度分量；

g0J——初始法向间隙；

q——轮轨在x3方向的接近量；

WJτ——J单元处轮轨界面相对刚性滑动量；

u——滑动量；

A0——矩形单元的面积；

bJ——单元中心处库伦极限摩擦力；

Ac——表示处于接触区内；

M——单元总数；

P——总法向力。

图2 矩形网格离散接触区

2 有限元计算模型

车轮和钢轨在相互作用区域中均要产生明显变形，可以将其看做是柔体－柔体的接触［7］。由于轮轨接触表面尺寸远小于接触表面的曲率半径，接触区域会出现非常大的应力集中，即接触区内以及接触区过渡到非接触区的部位将出现很大的应力梯度变化，因此，网格的精细程度将直接决定计算结果的精度。为得到较为精确的接触应力，接触区及其附近区域需要细化到一定的程度。而计算规模随着网格数量的增加，将成指数形式增长，致使计算成本太大。为避免出现这种情况，在离接触区较远的部分用较粗的网格进行划分，而接触区内部以及周边区域采用较细的网格［7－8］。

ANSYS在接触计算中，其面－面接触算法可以支持有大滑动和有摩擦的柔－柔大变形接触等问题的计算，能够为工程计算提供很好的计算结果［9］，因此，本文利用ANSYS软件模拟地铁轮轨的接触。采用一阶八节点六面体单元solid45模拟车轮及钢轨，采用接触单元CONTA174和TARGE170组成接触对，模拟车轮与钢轨的接触［10］。接触对之间的摩擦和运动形式采用库伦摩擦模型，摩擦系数取为0.3，接触算法采用扩展的拉格朗日算法。其有限元计算模型如图3所示，在ANSYS中建立了车轮的二分之一模型以及钢轨的局部模型，在钢轨的底面施加垂向和横向约束，在钢轨的断面施加纵向约束；在车轮轮毂的侧面施加横向约束，在轮毂孔的内侧面上施加垂向力。其接触区域的局部放大如图4所示。通过有限元计算，得到在不同轮对横移量条件下的轮轨接触应力。当轮对横移量为0mm时，其轮轨接触附近区域的von＿mises应力云图如图5所示，其接触区域及法向接触应力如图6所示。

图3 有限元计算模型

图4 接触区域局部细节放大图

图5 轨头接触附近von＿mises应力云图

图6 接触区域及法向接触应力

3 轮轨法向接触模型对比分析

利用MATLAB软件编制了轮轨赫兹接触计算程序，同时利用Kalker精确理论的数值程序CONTACT计算地铁车辆在不同轮对横移量下法向接触应力和接触斑面积，并与有限元分析结果进行比较。其中轮轨关系采用LM型车轮踏面和60kg／m级钢轨型面匹配，轴重为14t。轮轨接触面积及最大法向接触应力如表1所示，轮轨接触斑形状如图7所示，轮轨接触应力分布如图8～图10所示。

当轮对横移量为0时，由于接触斑内轮轨型面的曲率为常数，满足赫兹接触条件，因此赫兹接触、CONTACT以及有限元模型计算的接触斑形状比较接近，CONTACT结果较赫兹接触更接近于有限元计算结果；赫兹接触的最大接触应力达到1 438 MPa，分别较CONTACT和有限元接触大34.6%和12.6%；CONTACT与有限元模型的接触面积相差很小，而赫兹接触的接触面积最大。

当轮对横移量为5mm时，由于接触斑内轮轨型面的曲率不是常数，因此赫兹接触得到的接触斑形状与CONTACT和有限元模型相比有较大差异；CONTACT由于接触面积较大，因此最大接触应力最小；虽然赫兹接触与限元模型的接触面积和最大接触应力比较接近，但其分布范围不同。

表1 不同轮对模移量时轮轨间接触面积和最大法向接触应力

图7 轮轨接触斑形状

图8 yw＝0mm时轮轨法向接触应力分布

图9 yw＝5mm时轮轨法向接触应力分布

当轮对横移量为11mm时，发生轮缘接触，接触几何尺寸与接触斑尺寸相差不大，弹性半空间假设条件不再满足，因此赫兹接触和CONTACT的接触斑形状与有限元相比有较大差异；有限元模型的面积最大，几乎是赫兹接触和CONTACT的一倍，同时其最大接触应力最小，而赫兹接触的最大接触应力则远大于CONTACT和有限元接触模型。

图10 yw＝11mm时轮轨法向接触应力分布

综上，除了轮缘接触工况外，CONTACT的计算结果都比较接近有限元接触模型的计算结果，而赫兹接触的计算结果则有较大出入。虽然有限元方法能较为准确模拟轮轨法向接触问题，但缺点是计算速度较慢，在工程运用中受到限制，CONTACT也存在类似的问题。由于在轮轨磨耗及滚动接触疲劳的研究中需要对轮轨接触进行大量计算，因此轮轨法向接触模型的计算精度和计算速度应进行综合考虑。

4 结语

随着越来越多的城市开通地铁，地铁车辆的轮轨磨耗及滚动接触疲劳等问题一直困扰着运营管理者。本文基于赫兹接触理论、Kalker精确理论和有限元方法研究了地铁车辆轮轨法向接触问题，包括接触斑形状、接触面积和接触应力。在轮缘接触工况下，赫兹接触和CONTACT受弹性半空间假设限制导致计算结果与有限元接触相差较大，而在其余工况下，CONTACT的计算结果都比较接近有限元接触模型的计算结果。赫兹接触由于受接触斑内轮轨曲率为常数的限制导致其计算结果与CONTACT和有限元接触相比有较大出入。由于工程运用中需对轮轨接触进行大量计算，因此轮轨法向接触模型的计算精度和计算速度应进行综合考虑。

［1］Knothe K，Le T H.A contribution to calculation of contact stress distribution between elastic bodies of revolution with non－elliptical contact area［J］.Computers and structures，1984，18（6）：1025.

［2］Kalker J J.Three dimensional elastic bodies in rolling contact［M］.Dordrecht：Kluwer Academic Publisher，1990.

［3］Telliskivi T，Olofsson U.Contact mechanics analysis of measured wheel－rail profiles using the finite element method［J］.IMechE，2001：65.

［4］Sladkowski A，Sitarz M.Analysis of wheel－rail interaction using FE software［J］.Wear，2005，（258）：1217.

［5］Piotrowski J，kik W.A simplified model of wheel／rail contact mechanics for non－Hertzian problems and its applications in rail vehicle dynamic simulations ［J］.Vehicle System Dynamics，2008，（46）：27.

［6］金学松，刘启跃.轮轨摩擦学［M］.北京：中国铁道出版社，2004.

［7］张澎湃，井秀梅.轮轨接触应力的有限元计算［J］.铁道车辆，2007，45（6）：4.

［8］Yan W，Fischer F D.Applicability of the Hertz contact theory to rail－wheel contact problems［J］.Archive of applied mechanics，2000，70（4）：255.

［9］齐斐斐.30t轴重货车转向架关键技术研究［D］.成都：西南交通大学，2009.

［10］侯传伦.重载铁路曲线段磨耗状态下轮轨相互作用分析［D］.成都：西南交通大学，2009.