地铁双边供电系统建模与仿真

杨 阳 张士文 韩正之

（上海交通大学电子信息与电气工程学院，200240，上海∥第一作者，硕士研究生）

当需要规划一条新的地铁线路或者对原有线路设计进行调整时，我们就需要建立一个准确有效且能够快速响应负载变化的地铁仿真模型来对线路设计效果进行预测。在地铁系统仿真领域，前人已经做了大量的研究。一部分学者忽略了实际负载复杂的机械与电气特性，降低了仿真的真实性［1］；另一部分学者虽然提供了精确的列车负载模型、控制算法和运行参数［2］，但是他们缺少使用精确的直流接触电网模块来实时反映列车运行状况对电网的影响。

本文的重点之一在于建立了一个准确的直流接触电网模型，该模型的参数可以随着列车运行距离的变化而变化，从而模仿列车的行进；重点之二在于建立了一个简单而有效的列车负载模型，该模型对车轮与轨道之间复杂的动态交互过程进行了物理建模，并最终以电机角速度作为变量来实时模拟列车运行过程中负载的变化。利用以上仿真策略，本文对城市地铁供电系统进行了建模，仿真结果与实测数据基本吻合，这为进一步研究城市地铁系统打下了基础。

1 地铁供电系统

当今地铁供电系统普遍采用双边供电模式。如图1所示，110kV城市交流高压电源经过主变电站与牵引变电站两次变压后输出600V、650V、750V或1 500V直流电源（北京地铁直流牵引工作电压为750V，而本文研究的上海轨道交通直流牵引工作电压则为1 500V）作为列车牵引电源。该直流电通过列车受电弓进入车厢底部两点式电压型逆变器，经变压变频模式逆变后输出三相交流电为牵引电机供电，牵引电机转动进而带动列车前进。与此同时，电流经回流轨回流至变电站，由此组成城市地铁供电系统。

图1 地铁牵引供电系统原理图

2 直流接触电网等效模型

直流接触电网在地铁供电系统中扮演着极其重要的角色。由牵引变电站送出的1 500V直流电压经过直流馈线到达直流电网。通过受电弓，行进过程中的列车将直流电压引入逆变器进行逆变，从而驱动牵引电机工作。根据Fracchia所作的研究，直流接触电网等效模型可由等效阻抗代替，其等效电路如图2所示，各部分参数如表1所示。在实际中，直流接触电网的电气特性是随着列车运行距离而变化的。然而，前人所做的研究都仅仅把直流侧电网等效为一个阻值恒定的电阻，这种做法降低了仿真的真实性。因此，本文搭建了一个时变的直流接触电网模型来反映地铁实际运行过程中直流侧电网对整个供电系统的影响，提高了仿真的真实性。

图2 PSB直流接触电网模型

表1 直流接触电网模型参数

为了使模型参数随列车的行进距离同步变化，本文利用电流控制电压源搭建了可变电阻，而可变电阻的搭建使用分段投切的方法。原理如下所示。

首先求出列车行驶距离，公式如下：

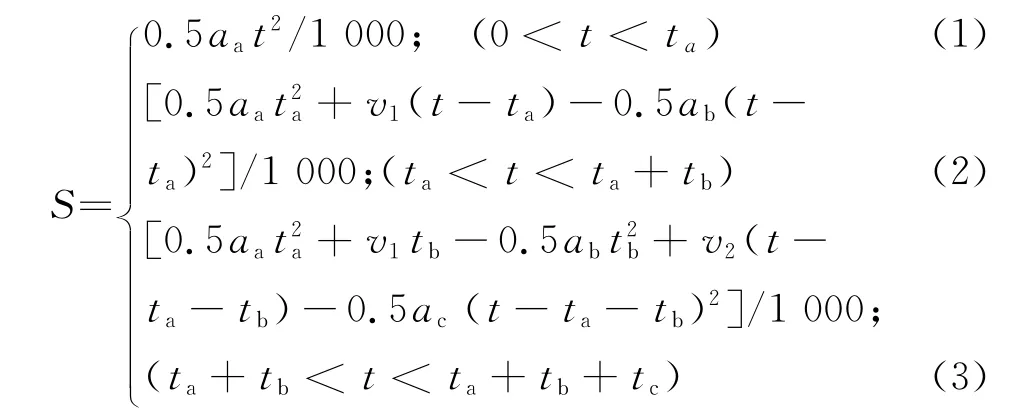
式中：

v1——列车设定速度，m／s；

aa——列车加速度，m／s2；

ta——加速时间，ta＝v1／aa，s；

tb——惰行时间，s；

tc——制动时间，s；

ab——惰行加速度，m／s2；

v2——列车惰行结束后速度，v2＝v1－abtb，m／s；

ac——制动加速度，m／s2。

求出列车行进距离S后，便可以S为变量，利用PSB中受控源搭建可变电阻，模型如图3所示。

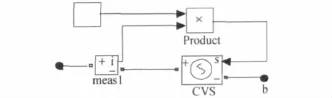
图3 可变电阻模型

由图3可得公式：

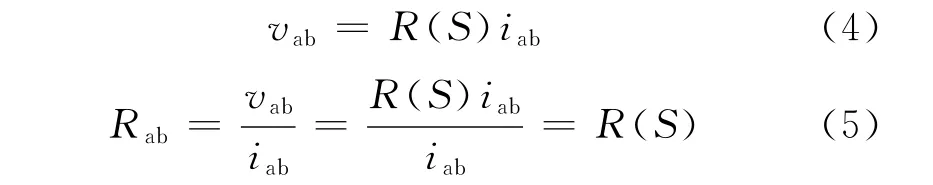
由此可见，a，b两端电阻能随着距离S的变化而变化，本文利用该模型搭建了时变的直流接触电网模型。

3 列车负载模型

在列车实际运行过程中，车轮与轨道之间的动态交互过程受多种因素影响。因此，需要建立一个精确的负载模型，使其能够准确并快速地反映实际负载的变化。在现今对列车负载模型的研究中，很多学者将该模型等效为一个简单的电流源，该方法对于研究多列列车同时进出站对电网电压的影响具有较好的效果；另一种做法是学者Steven Senini在其论文中提出的，他对车轮与轨道之间的动态交互过程进行了复杂的数学建模，考虑了两者之间的黏附效应以及滑移流效应，然而该方法包含了复杂的积分和微分方程，响应速度较慢，不利于系统动态响应的瞬时性；本文运用了学者黄云鹏在其论文中提到的方法［2］，该方法利用电机角速度作为变量，实时反应列车负载在行进过程中的动态变化过程。

由图4可得列车牵引传动的基本原理：交流电机输出转矩作用于车轮，提供列车前进牵引力，同时在列车对轨道的正向压力作用下，车轮对轨道产生相对运动趋势，由此产生轨道对车轮的反作用力驱使列车运动。

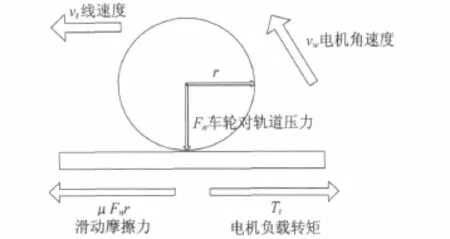
图4 轮对与轨道受力分析图

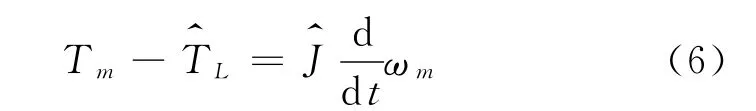
式中：

Tm——电机输出转矩，Nm；

ωm——电机角速度，rad／s。

接下来，对车轮与轨道间动态交互过程进行受力分析。首先研究车轮与轨道之间的相互作用。由图4可得如下公式：

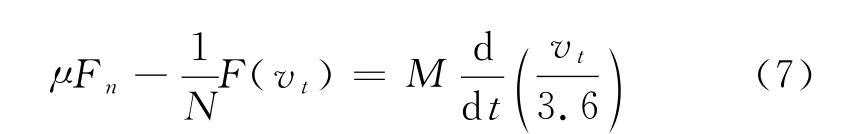
首先建立如下公式：

式中：

Fn——单个轮轴对轨道的正向压力，N；

μ——粘着系数；

F（vt）——列车运行阻力，N；

M——单位车轴分担的车辆质量，kg；

vt——车速，km／h；

N——电机数，台。

其次对于牵引电机，有如下公式成立：

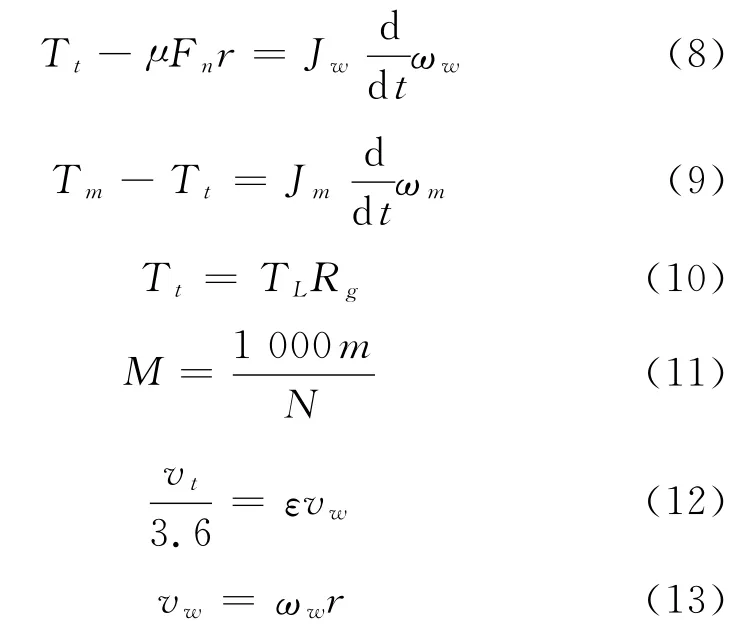
式中：

TL——列车负载转矩，Nm；

Tt——电机负载转矩，Nm；

Jw——车轮转动惯量，kg·m2；

Jm——电机转动惯量，kg·m2；

ωw——车轮角速度，rad／s；

Rg——传动比；

m——列车总质量，kg；

r——车轮半径，m；

ε——蠕滑率。

由式（6）～（13）可得如下公式：

与式（6）对比，可得等效转矩为：

轨道车辆阻力经验公式为：

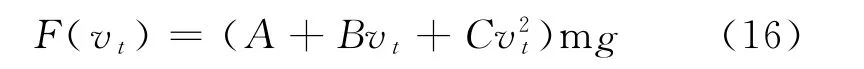
其中，A＝1.28，B＝0.0012，C＝0.000195。

上海轨道交通2号线车辆参数为m＝220×103kg（空载），r＝0.42m，N＝24 台，Rg＝3.036，ε＝0.995，将参数带入公式（17）得：

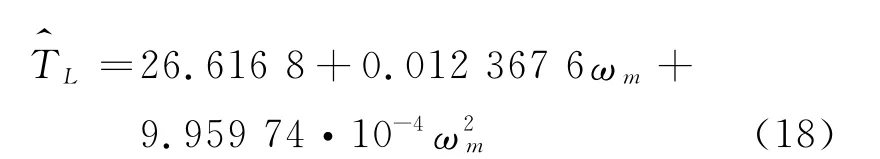
由此，列车电机等效负载转化为以ωm为变量的一元二次方程。这样，就能利用电机角速度作为输入变量来搭建电机等效负载。

4 地铁牵引供电系统PSB模型

图5给出了地铁牵引供电系统PSB模型，其原理如下：

（1）牵引变电站1、2中牵引变压器变比为33 kV／1.22kV，三相绕组接线方式为 D11／Y／D11。两路33kV三相交流电源分别有±7.5°的相位移，经过两组12脉波整流电路形成1 500V24脉波直流电压作为列车直流电源。

（2）直流接触电网模块1、2分别位于牵引变电站1、2侧。当列车运行时，电网模块1中参数正比于列车运行距离，电网模块2中参数反比于运行距离。

（3）DC－AC逆变器，异步感应电机 M与DTC控制器三者组成闭环模拟实际列车运行过程中的电气与机械特性。

（4）利用电机角速度作为变量构造了等效负载模块，将计算所得转矩反馈至电机负载转矩端口形成闭环。

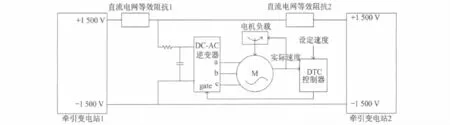
图5 地铁牵引供电系统PSB模型

5 仿真过程与结果

5.1 地铁实际运行数据采集

本文利用美国NI公司生产的PCI－6025数据采集卡、SCXI－1000信号调理器以及上海轨道交通2号线车辆自带的电压与电流传感器采集了直流侧母线电压、电流。采集数据如下图6、7所示。

图6 实测直流母线电压

图7 实测直流母线电流

由图6可见，在测试时间10s时，列车从静止开始加速，进入牵引阶段，此时电网电压下降；30s时，牵引阶段结束，车速到达指定60km／h，逆变器关闭，列车进入惰行阶段，此时电网电压抬升；37s时，惰行结束，列车进入制动阶段，电机向电网反馈电能，由于这部分能量没有被线路上别的列车吸收，且变电站采用不控整流装置，能量无法回流，这导致电网电压升高，当母线电压超过1 800V时，列车电阻装置开启，使电网电压维持在1 800V；50s后，列车停止，母线电压恢复到正常水平。

5.2 仿真结果

图8、9、10分别为电机转速、直流电网电压与电流仿真结果。

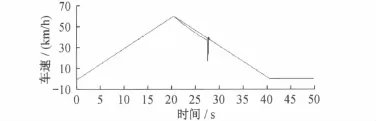
图8 电机转速仿真结果

图9 直流母线电压仿真结果

图10 直流母线电流仿真结果

由图8～图10可知：

（1）0.5s～20.5s为牵引阶段，电机消耗电能提供牵引力，列车匀加速前进，直流侧电网电压从1 700V下降到1 500V左右，并且随着列车速度的增加，功率随之上升，因此电流从0A逐渐增大到300A。

（2）20.5s～27.5s为惰行阶段，此时逆变器关闭，电机不消耗功率，因此直流侧电网电压上升，直流侧电流为0，列车在惯性下前进，由于存在摩擦力，列车减速运行。

（3）27.5s～40.5s为制动阶段，列车转矩与功率均变负，电机回馈电能，电流反向，电网电压上升至1 800V，这时由于刹车斩波器的存在将电压钳位于1 800V。

（4）40.5s～50s为静止阶段，电机停止工作，不再回馈电能，电网电压下降至1 700V。

将仿真结果与实测数据对比可知仿真波形和实测曲线十分相似，细微上的差别可能是由于实际列车运行过程中的各种干扰和电网电压的波动所造成的。

6 结语

本文利用PSB／Matlab搭建了城市地铁系统双边供电模型。经验证，仿真结果与实际相吻合，这说明本文所用的直流接触电网等效模型与列车电机负载等效模型在仿真实际列车运行时起到了良好的效果。由此我们便可以该模型为基础，对城市地铁系统做进一步的研究。例如通过计算列车不同运行阶段的能量消耗来优化列车加速、惰行及制动的时间分配，从而提高运行效率；通过并联更多的列车，可以研究多列车运行对电网的影响，这对于优化列车进出站次序有着较大意义。

［1］Martyn Z，Alasdair C，Holden J.Modeling Electrified Transit Systems ［J］.IEEE TRANSACTIONS ON VEHICULAR TECHNOLOGY，2010，59（6）：2748.

［2］黄云鹏，赵坤，陆峰.轨道车辆牵引电机负载模拟系统建模及仿真［J］.微计算机信息，2010（13）：161.

［3］毛明平，陶生桂，王曰凡.上海地铁2号线牵引仿真计算研究［J］.城市轨道交通研究，2001，4（2）：22.

［4］徐国卿.城市轨道车辆电力传动［M］.上海：上海科学技术出版社，2003.