基于液体缩尺模型的地铁活塞风与站台送风耦合

刘佳妮 沈 丽 唐道发 罗 成 杜晓明

（上海理工大学环境与建筑学院，200093，上海∥第一作者，助理工程师）

1 试验台及试验方案

1.1 试验原理

由流体力学相似性原理可知，要保证两个流动的力学相似，就必须使两个流动的几何相似、运动相似，动力相似、以及两个流动的边界条件和起始条件相似。但是在模型几何尺寸和流动介质等发生变化不同于原型时，很难保证所有的相似准则数同时对应相等。因此，应抓住对流动起决定性作用的力，保持原型和模型中该力的相应准则数相等。

实际情况中，活塞风与站台送风射流因温差较小，密度相差不大，因此可以认为实际中耦合气流所受重力与浮力相平衡。模型试验中可不考虑弗诺得数的影响；且实际中活塞风与站台送风射流速度较大，流动处于自模区，这时模型设计不受模型律制约，即只需满足模型流动同时进入自模区，就可以实现模型和原型流动在速度分布上的相似，达到用模型试验模拟原型流动的目的。

1.2 试验台简介

本试验通过搭建液体示踪缩尺模型试验台，运用液体代替气体模拟闭式系统列车活塞风与站台送风射流的耦合气流，并对其气流组织的速度场与流线进行研究。原理图如图1所示。

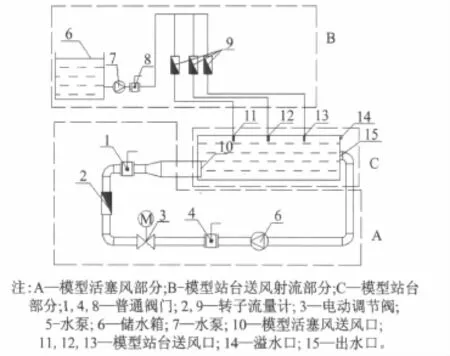
图1 试验原理图

本模型试验，以上海南京西路地铁车站站台层为原型搭建1∶16的缩尺模型实验台，原型与模型几何尺寸对应表见表1。

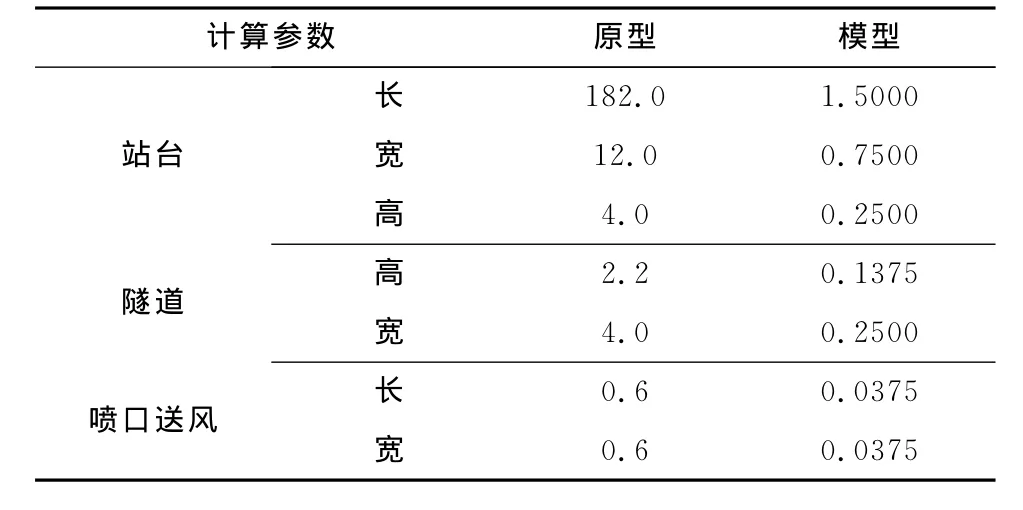
表1 站台原型与模型装置几何尺寸对应表 m

通过现场实测，在列车入口处的活塞风最大风速为7.6m／s，送风口风速约为6m／s，故分别选取活塞风与站台送风射流的最大上限风速为8m／s，均满足试验要求。原型中，隧道和送风口的当量直径分别为2.84m和0.6m。以原型中选取活塞风和空调送风风速均为2m／s为例，对应的Re（雷诺数）分别为3 616 197和76 433，均处于自模区。模型试验中，需运用圆管代替站台隧道口和方形空调送风口，按照等面积的原则，可以计算得出相应半径分别为0.105m和0.02m，查PVC（聚氯乙烯）管规格分别选择公称直径为200mm和40mm的管件。由流体力学可知，当液体流动进入紊流状态时，管道断面流速分布比较均匀，能够实现模型中站台送风射流的均匀送风要求。选择Re＝2 400，求得此时模型站台送风射流水速为0.06m／s，因此选取流速值v＝0.06m／s模拟原型0.84m／s的风速，故得速度比例尺为λv＝0.06／0.84＝1∶14。同理，可得送风口和隧道口的流体在原型与模型中的速度和雷诺数（对应表分别如表2和表3所示）。

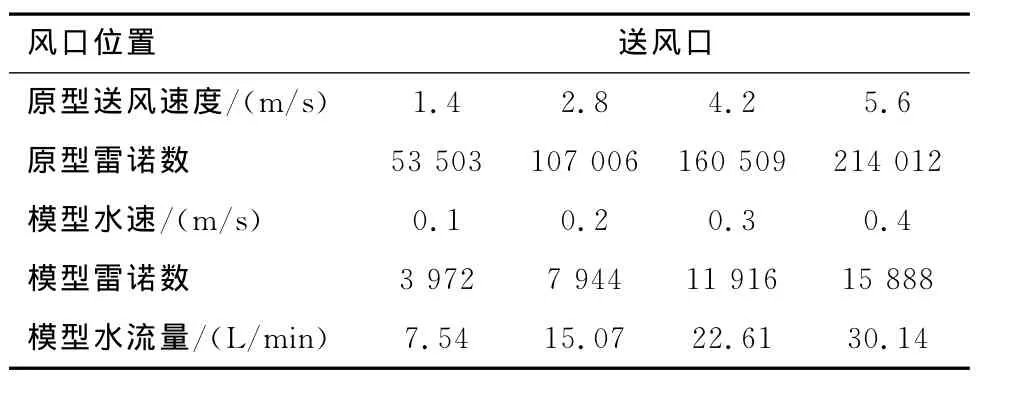
表2 送风口原型与模型参数表

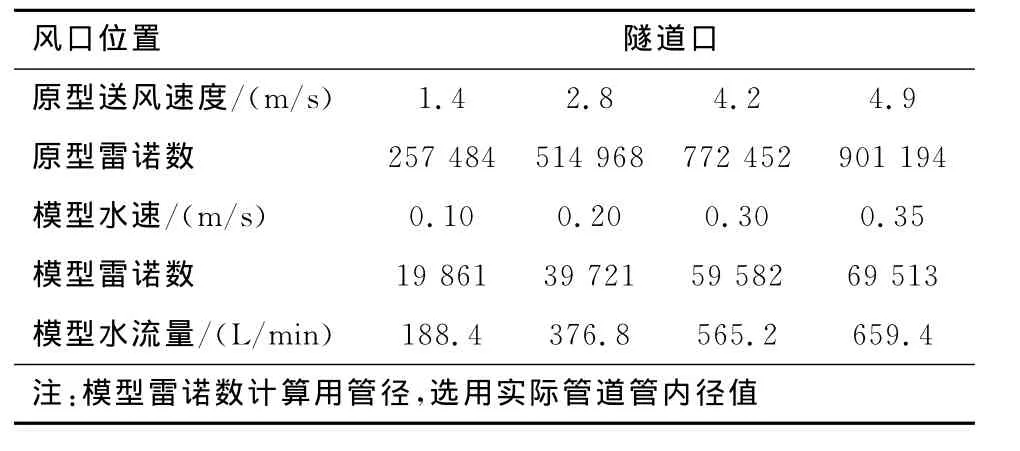
表3 隧道口原型与模型参数表

1.3 试验方案

为了能够得到活塞风与站台送风射流的耦合轨迹，试验中利用红色色素调节站台送风射流水箱中液体颜色，以便试验中观察活塞风与站台送风射流耦合的轨迹。在轨迹线上布置测点9、10，测点布置如图2所示。

本试验所用仪器有转子流量计、循环水泵、电动阀门、LGY—Ⅲ型多功能智能流速仪等，其中LGY—Ⅲ型多功能智能流速仪用于测量耦合流场水流速度。

试验流程粗选I作业为铜钼等可浮（优先浮选），粗选II为强化浮选，通过采用黄药或其他强捕收力的药剂进行强化捕收，提高目的矿物回收率。此次试验进行了四种药剂的对比，试验结果见图10。从试验结果可以看出，采用丁黄药与BK404B组合时，铜、钼作业回收率较高。

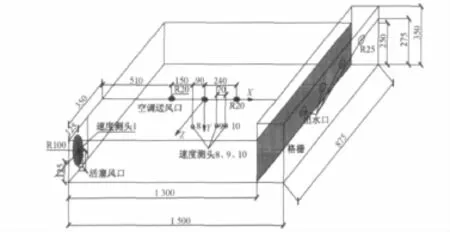
图2 模型试验台测点布置（单位：mm）

2 试验结果与分析

2.1 活塞风流量变化曲线

为了模拟活塞风的变化规律，根据地铁的实际运行规律及缩尺模型时间比例尺，将电动阀设置成加速时间、匀速时间和减速时间，分别为33s、31s和33s。通过调节回水管上的调节阀，控制活塞风的流量值来模拟活塞风射流加速、匀速和减速过程，由速度测点1测得活塞风速度变化从而求出其流量变化。由图3与图4可知，本模型试验的活塞风射流满足文献12对隧道活塞风的实测［12］。

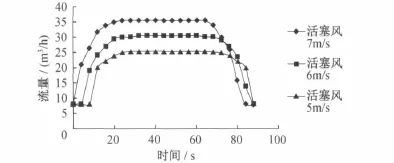
图3 模型试验活塞风流量变化曲线

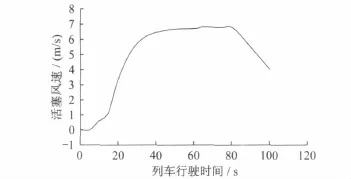
图4 文献12活塞风实测流量变化曲线

2.2 活塞风与站台送风射流速度的耦合轨迹

为了试验的方便，选择活塞风与站台送风射流均恒定的工况。纵横坐标分别表示距离站台送风射流风口的垂直和水平方向的距离，其中刻度0位置为站台送风口的位置，横坐标上坐标距离8cm、15cm处分别是测点9、10的位置。活塞风速分别为5m／s、6m／s、7m／s时活塞风与站台送风射流的耦合曲线如图5、图6、图7所示。

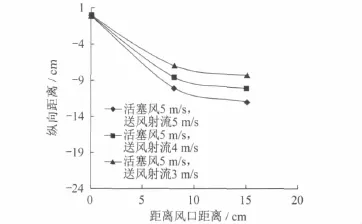
图5 活塞风与站台逆风射流的耦合曲线（活塞风速为5m／s）

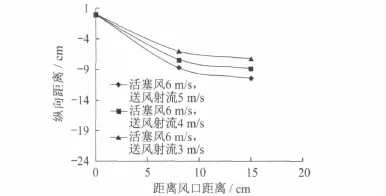
图6 活塞风与站台逆风射流的耦合曲线（活塞风速为6m／s）

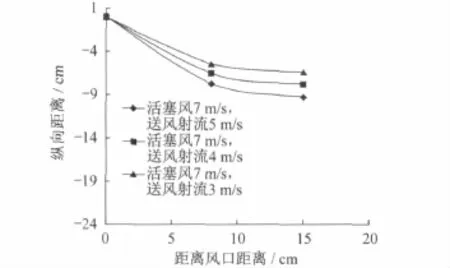
图7 活塞风与站台逆风射流的耦合曲线（活塞风速为7m／s）

由图5、图6、图7可知，在活塞风速度一定的情况下，站台送风射流速度越小，活塞风与站台送风射流的耦合轨迹越平缓。

在文献13中，设横流的流速为ua，射流出口断面直径为D，射流出口射流流速为u0，两者的比值为R＝u0／ua，垂直于横流与射流断的射流中心线方程为z／（R×D）＝2.05×［x／（R×D）］0.28。此处的横流相当于试验台上的活塞风，射流相当于实验台上的站台送风射流，将其带入射流中心线的方程内，计算得出的轨迹规律与本试验台活塞风与站台送风射流速度耦合轨迹图基本相吻合。

2.3 活塞风最大值不变，改变站台送风射流速度

保持活塞风速度最大值不变，改变站台送风射流速度，观察在活塞风一定的情况下，不同站台送风射流对各个测点速度的影响。活塞风速度最大值为6m／s，站台送风射流流速分别为3m／s、4m／s、5 m／s时各测点的速度分布及对应的拟合曲线如图8、图9、图10所示。

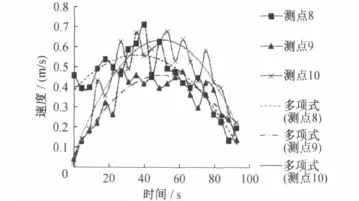
图8 各测点的速度分布图（站台送风射流流速为3m／s）

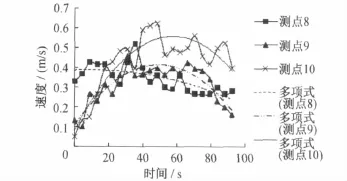
图9 各测点的速度分布图（站台送风射流流速为4m／s）

其中测点8是风口前面的测点，即未耦合的测点，测点9和测点10是风口依次往后的测点，即活塞风与站台送风射流耦合后的测点。

通过对图8、图9、图10观察和对比，在活塞风最大值为6m／s时可总结如下：

（1）站台送风射流流速分别为3m／s、4m／s和5 m／s时，各测点速度变化曲线随着活塞风增大、稳定、减小的过程，与实测活塞风变化曲线相吻合较好。

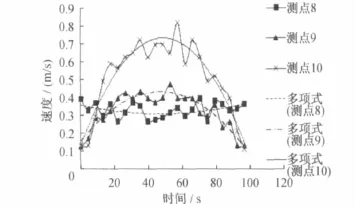
图10 各测点的速度分布图（站台送风射流流速为5m／s）

（2）改变站台送风射流速度值的情况下，测点8的速度改变较剧烈，规律不明显。

（3）改变站台送风射流速度值的情况下，测点9的速度随着站台送风射流流速的增大，速度反而逐渐变小。

（4）改变站台送风射流速度值的情况下，测点10的速度随着站台送风射流流速的增大，速度逐渐增大。

2.4 站台送风射流流速不变，改变活塞风速度

取站台送风射流流速为3m／s，活塞风速最大值分别为5m／s、6m／s、7m／s，各测点的速度分布如图11、图12、图13所示。

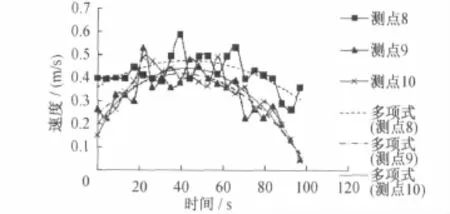
图11 各测点的速度分布图（活塞风速最大值为5m／s）

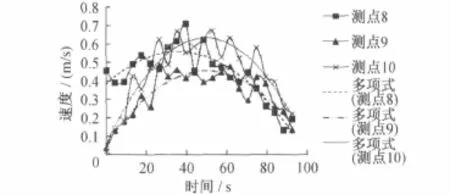
图12 各测点的速度分布图（活塞风速最大值为6m／s）

通过对图11、图12、图13观察和对比，在站台送风射流流速为3m／s，活塞风速最大值分别为5 m／s、6m／s和7m／s时可总结如下：

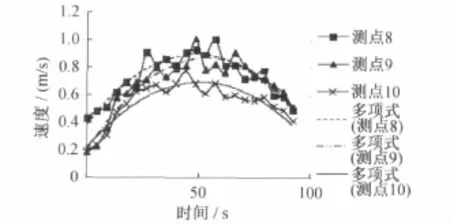
图13 各测点的速度分布图（活塞风速最大值为7m／s）

（1）各测点速度变化曲线随着活塞风增大、稳定、减小的这个过程，与活塞风变化曲线相吻合较好。

（2）随着活塞风速度最大值的增大，测点8速度值曲线改变较平缓且测点8的速度值随着活塞风的增大而增大。

（3）测点9速度曲线改变较剧烈且测点9的速度值随着活塞风速最大值的增大而增大。

（4）测点10速度曲线改变剧烈且测点10的速度值随着活塞风速最大值的增大先增大后减小。

3 结语

（1）试验中各测点速度变化曲线随着活塞风增大、稳定、减小的这个过程，基本上与实测活塞变化曲线相吻合。

（2）隧道入口处活塞风初始速度越大，入口后站台各测点速度会随之增大。

（3）不同活塞风初始值情况下，距隧道入口不同距离的各测量横断面上速度分布具有相似性。

（4）在活塞风一定的情况下，站台送风射流速度越小，活塞风与站台送风射流的耦合轨迹越平缓；在站台送风射流一定的情况下，活塞风越小，活塞风与站台送风射流的耦合轨迹越陡。

由以上结论可知，在非屏蔽门系统的地铁实际运营过程中，可以适当打开在站台两端活塞风的通风井，并增大站台送风射流流速以达到舒适节能的目的。

［1］OUYANG Q，JIANG Y，Z Y X.Calculation of critical ventilation velocity for the train jam in subway tunnel using CFD simulations［C］／／Proceedings of the 2002International Symposium on Safety Science and Technology（2002ISSST）.Tai’an，China：Safety Science and Technology，2002：1363.

［2］沈翔，吴喜平.地铁活塞风特性的测试研究［J］.暖通空调，2005（3）：103.

［3］王丽慧，吴喜平.地铁车站环控温度场的研究［J］.制冷空调与电力机械，2007（28）：30.

［4］王丽慧，吴喜平.地铁活塞风对车站环控速度场的影响［J］.地下空间与工程学报，2007（2）：161.

［5］贾力，黄鹏，杨立新.地铁车站内流动特性的数值模拟［J］.北京交通大学学报，2008，32（1）：83.

［6］Ren M L，Chen C，Guo Q，et al.Numerical analysis and effectively using of piston－effect in subway［J］.Shanghai Jiaotong Daxue Xuebao，2008，42（8）：1376.

［7］袁凤东，由世俊，杨向劲.地铁侧式站台空调气流CFD模拟［J］.西南交通大学学报，2005（6）：303.

［8］毛军，郗艳红，吕华，等.数值模拟与仿真在地铁火灾防灾减灾中的应用［J］.北京交通大学学报，2008，32（4）：52.

［9］杨晖，贾力，黄培雷.列车运动对地铁站台环境影响的数值模拟［J］.地下空间与工程学报，2010（2）：270.

［10］杨晖，贾力，杨立新.列车运动对地铁站台空气温度分布动态影响的数值分析［J］.北京交通大学学报，2009（1）：37.

［11］荣莉.姚杨，姜益强，等.侧式站台和岛式站台活塞风特性分析比较［J］.建筑热能通风空调，2007，26（4）：87.

［12］沈翔，吴喜平，董志周.地铁活塞风特性的测试研究［J］.暖通空调，2005，35（3）：104.

［13］余常昭.紊动射流［M］.北京：高等教育出版社，1993.

［14］吴炜，彭金龙.快速地铁隧道空气动力学效应研究［J］.城市轨道交通研究，2011（12）：37.