含玻璃微球的黏弹性复合材料覆盖层的水下吸声性能分析

2013-09-25于利刚李朝晖王仁乾马黎黎

物理学报 2013年6期

于利刚李朝晖王仁乾马黎黎

1 引言

水下吸声覆盖层在水声学领域的应用比较广泛,特别是对潜艇的隐身具有重要的意义,因此,相关的研究一直得到了广泛的关注.如何提高低频吸声性能,是水下吸声覆盖层研究的难点.为了提高低频吸声性能,传统的吸声覆盖层中通常含有宏观的空腔结构[1,2],但是宏观的空腔结构的引入会降低覆盖层的高频吸声性能和耐高压性能.近年来,一些新兴的声学理论和材料在水下吸声覆盖层方面的应用研究得到了发展.声子晶体理论是近年来声学领域研究的热点,该理论在水下吸声覆盖层的应用得到了尝试[3-7].声子晶体覆盖层中含有周期性结构,其共振吸声可以提高覆盖层的低频吸声性能.随着压电聚合物材料性能的不断提高,压电聚合物材料成为发展智能型水下吸声覆盖层的理想材料.聚合物压电材料不仅可以通过机械阻尼吸声,还可以通过压电效应将声波转换为电能,由分流电路损耗掉[9-11].另外,充满黏滞流体的多孔金属板也是一种新型的水下吸声材料.研究表明,选择合适的黏滞流体,采用较薄的多孔金属板就可以获得很好的低频吸声性能[12].虽然新兴声学理论和材料在水下覆盖层方面的应用研究取得一定的进展,但是满足到实际应用的要求,还需要较长的时间.

相比较而言,较为传统的理论和材料在水下吸声覆盖层的应用研究仍具有一定的潜力.含有微小空气腔体的黏弹性复合材料一直是水声领域的研究热点[13-24].微小的空气腔体的引入可以改变黏弹性聚合物复合材料的特性声阻抗,也可以提高材料的机械阻尼.为了保持复合材料的耐压性能,微小空气腔体由玻璃球壳包覆.玻璃微球的直径一般为几十微米,远远小于入射声波的波长,因此认为复合材料的性质均匀.Baird等[19]指出利用含玻璃微球的黏弹性复合材料,采用等效参数的方法,优化设计多层结构的水下吸声覆盖层,但是到目前为止相关的研究并不多见.

本文对含有玻璃微球的黏弹性复合材料覆盖层的水下吸声性能进行了理论分析.采用Haberman[20]的等效参数方法分析了玻璃微球的体积含量对复合材料力学和声学性能的影响.采用声波在多层介质中传播的一维模型,分析了玻璃微球体积含量对复合材料覆盖层吸声性能的影响,以提高覆盖层的低频吸声性能,同时保证高频吸声系数大于某一限值(0.7)为优化目标,采用遗传算法对玻璃微球体积含量在覆盖层厚度方向上的分布进行优化.从声阻抗匹配的角度分析了多层优化结构提高吸声性能的机理.另外,借鉴橡胶行业的生产技术,简单分析了以含玻璃微球的复合材料为原材料,制备多层优化结构覆盖层的生产工艺.

2 黏弹性复合材料的力学和声学参数与玻璃微球体积含量的关系

2.1 等效参数模型

Haberman等[20]采用自洽理论推导出含玻璃微球的黏弹性复合材料的等效力学参数公式(1)—(8),计算了不同玻璃微球体积含量的复合材料板对水下声波的传输损耗,但是没有计算复合材料的力学和声学参数.为了更好地了解玻璃微球对复合材料力学和声学性质的影响,本文采用Haberman的公式分析了玻璃微球体积含量对复合材料力学和声学性质的影响.

图1为含玻璃微球的黏弹性复合材料的微观结构示意图.µ,λ,K为拉梅常数、剪切模量和体积压缩模量,上标eff,M,C,I分别为复合材料、聚合物基材(Matrix)、玻璃球壳(Coating)、球壳内包含的(Inclusion)空气.fI为玻璃球壳中的空气在复合材料中占的体积比,Δa/a为球壳的厚度和半径之比.σ为泊松比,上标x在具体计算中将会被eff,M,C,I代替.本文采用了文献[19]给定的聚合物基材、玻璃和空气的参数.表1,2分别为黏弹性聚合物的和玻璃微球的参数.

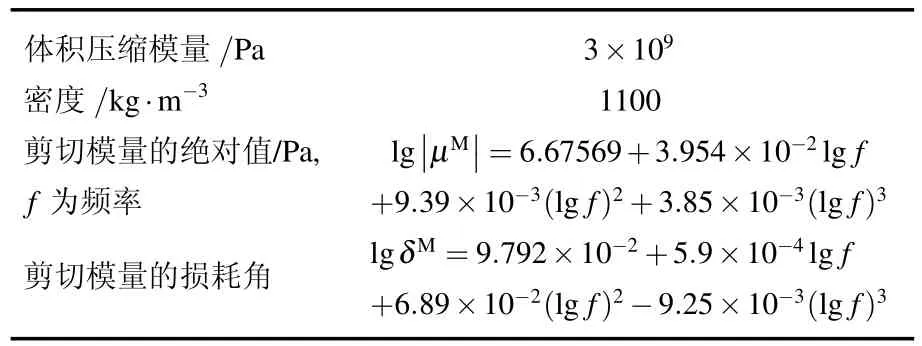
表1 黏弹性聚合物的力学参数

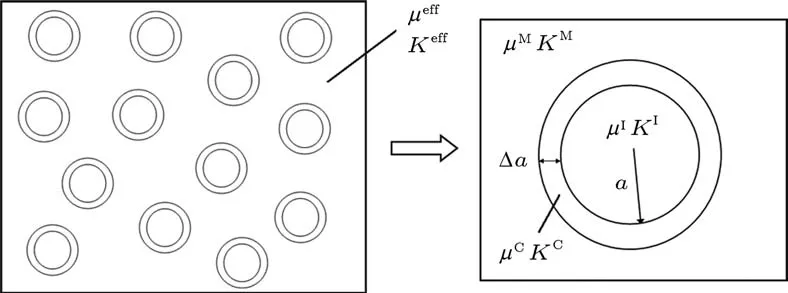
图1 含玻璃微球的黏弹性复合材料的微观结构示意图

采用迭代法可以计算出含玻璃微球的黏弹性复合材料的体积模量Keff和剪切模量µeff,而复合材料的密度、纵波波速分别为

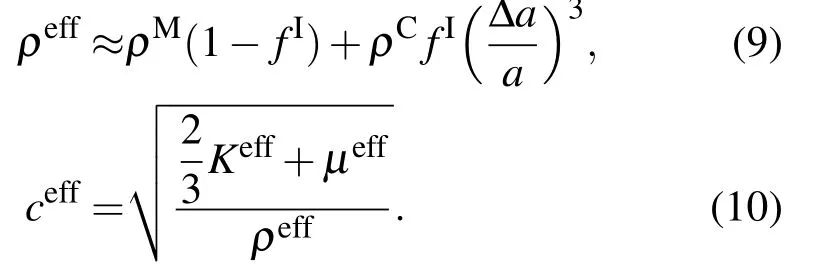
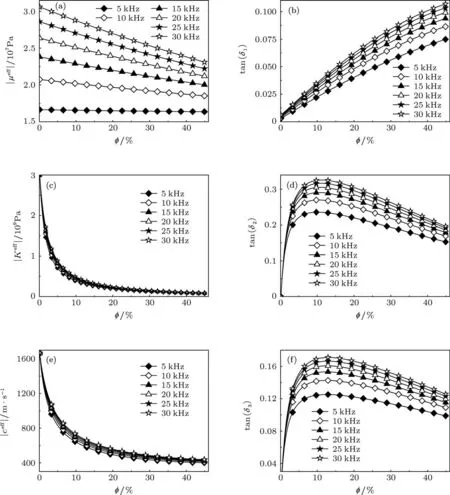
图2 不同频率下(f=5,10,15,20,25,30 kHz)复合材料的力学和声学参数随玻璃微球的体积含量的变化 (a),(b)为剪切模量的绝对值和损耗角的正切值tan(δ1);(c),(d)为体积模量的绝对值和损耗角的正切值 tan(δ2);(e),(f)为纵波声速的绝对值和损耗角的正切值 tan(δ3)

2.2 数值计算结果与分析

由于黏弹性聚合物材料的力学和声学参数是频率 f的函数,因此计算了不同频率(f=5,10,15,20,25,30 kHz)下,复合材料的力学和声学参数随体积含量φ的变化.如图2(a),(b)所示,复合材料的剪切模量的绝对值和损耗角正切值 tan(δ1)随频率的升高而增大,增大的幅度随频率的升高而减小.在 f较低的情况下,随 φ 的变化不大;在频率较高的情况下,会随 φ 的升高而减小,近似线性变化.而剪切模量损耗角的正切值tan(δ1)随φ的升高而增大,在φ较大时近似线性变化.如图2(c)所示,不同频率的体积模量的绝对值几乎是重合的,说明随频率的变化不大.当φ较小时,随着 φ 的增加而显著减小;而当 φ 较大时,随着 φ 的增大而缓慢减小.如图2(d)所示,复合材料的体积模量损耗角的正切值tan(δ2)随频率的升高而增大,增大的幅度随频率的升高而减小.当φ较小时,tan(δ2)随着φ的升高而显著增大;当φ较大时,tan(δ2)随着φ的升高而缓慢增大;当φ≈10%时,tan(δ2)到达最大值;φ继续增大,tan(δ2)逐渐减小.对比图2(a),(c)可以看出,大约比大两个数量级.对比图 2(b),(d)可以看出,虽然当φ=0时,tan(δ2)=0,但是当φ增加,tan(δ2)比 tan(δ1)大很多.例如φ=10%,f=10 kHz时,tan(δ1)和 tan(δ2)分别为 0.0275 和0.270,相差接近一个数量级.因此,如图2(e),(f)所示,复合材料纵波声速随φ的变化趋势与体积模量相似.总之,由于玻璃微球的引入,黏弹性复合材料的力学和声学阻尼会显著增加.由于玻璃微球的体积含量φ在一定范围的变化可以显著影响复合材料的声学性质,可以通过改变玻璃微球的体积含量形成多种声学性质不同的复合材料.

3 含玻璃微球的黏弹性复合材料吸声性能分析

3.1 声波在多层介质中传播的一维模型

本文参考声波在多层介质中的传播理论[25]针对水下覆盖层的边界条件,建立声波在多层黏弹性复合材料中传播的一维模型.如图3所示,假设N层黏弹性复合材料粘贴在一层钢板上,复合材料和水接触,而钢板和空气接触,复合材料和钢板的横向尺寸远大于其厚度,水和空气为半无限大空间.当声波由水中垂直入射到复合材料覆盖层上,在各个界面上发生反射和透射.设界面1的声压和质点振速为P1,U1界面2的声压和质点振速为P2,U2两个界面的声压和质点振速的关系可以表示为

其中ρ1c1为第一层复合材料覆盖层的特性声阻抗,l1为覆盖层的厚度,k1=ω/c1为波数,c1为复合材料中的纵波声速,B1为声压和质点振速的传递矩阵.同理,界面1与界面3的声压和质点振速的关系为

B2为第二层复合材料的声压和质点振速的传递矩阵.同理,界面1与界面N+2的声压和质点振速的关系

BN+1为钢板的声压和质点振速的传递矩阵.界面1的表面声阻抗为

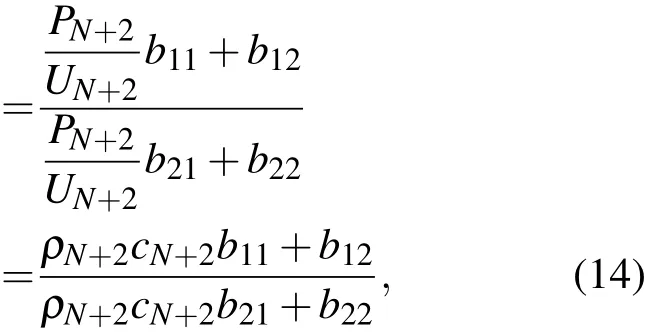
ρN+2cN+2为空气的特性声阻抗.界面1的反射系数为

吸声系数为

P1i,P1r为界面1的入射声压和反射声压.界面1的表面声阻抗Z1为复数,可表示为：Z1=Zr1+jZi1·ρ0c0为水的特性声阻抗,声波在水中的损耗很小,水的特性声阻抗可以看作实数.通常要达到好的吸声效果,吸声材料要有较高的机械阻尼,其特性声阻抗要与吸声体系中的其他介质相匹配.

图3 声波在多层黏弹性复合材料覆盖层中传播的示意图

3.2 玻璃微球体积含量对单层结构覆盖层的吸声性能的影响

应用声波在多层介质中传播的一维模型,分析了玻璃微球的体积含量φ对单层结构覆盖层的吸声性能的影响.单层结构覆盖层的厚度l=10 mm,而水和钢板的参数如表3所示.为了突出覆盖层的低频吸声性能,横坐标频率 f采用对数坐标.当聚合物中玻璃微球的体积含量φ=0%,覆盖层的吸声系数α很小.当φ增大到5%,α会显著提高.随着φ的进一步增大,α随频率变化的起伏较大.α在低频的共振峰会移向更低频率,带宽变窄,高频的吸声系数降低.当φ由5%增大到10%时,α在低频共振峰值升高;当φ由10%增大到25%时,低频共振峰值逐渐降低.低频共振峰值随φ的变化,与声速损耗角的正切值随φ的变化相一致.随着φ的增大,吸声系数峰值之间的极小值显著降低.例如,φ=25%时,3450 Hz对应的吸声系数只有0.40.总之,随着φ的增大,吸声系数在低频的峰值会移向更低的频率,峰值先升高,然后逐渐降低.随着φ的增大,较高频率的吸声系数降低.含玻璃微球的黏弹性复合材料覆盖层的低频和高频吸声性能存在一定的矛盾,在应用过程中,需要平衡低频和高频吸声性能.

表3 水、钢板和空气的参数

3.3 玻璃微球体积含量在覆盖层厚度方向的分布对吸声性能的影响

为了平衡复合材料覆盖层的低频和高频吸声性能,本文将玻璃微球的体积含量在覆盖层厚度方向的分布进行了优化,在一些关键的频段改善覆盖层表面和水的声阻抗匹配.将复合材料根据玻璃微球的体积含量φ从0到30%,以0.5%的间隔形成61种不同复合材料.将吸声覆盖层在厚度方向上等分成N层,每一层所用的材料可以从61种不同的复合材料中选取.虽然声学中对多层声阻抗匹配的问题已有较为成熟的理论[26,27],但是通常理论上要求的匹配材料在现实中不存在,因此本文采用遗传算法对复合材料在厚度方向的分布进行了优化.遗传算法优点是只须设定优化的目标,可以避开具体的物理过程,达到优化的目的.

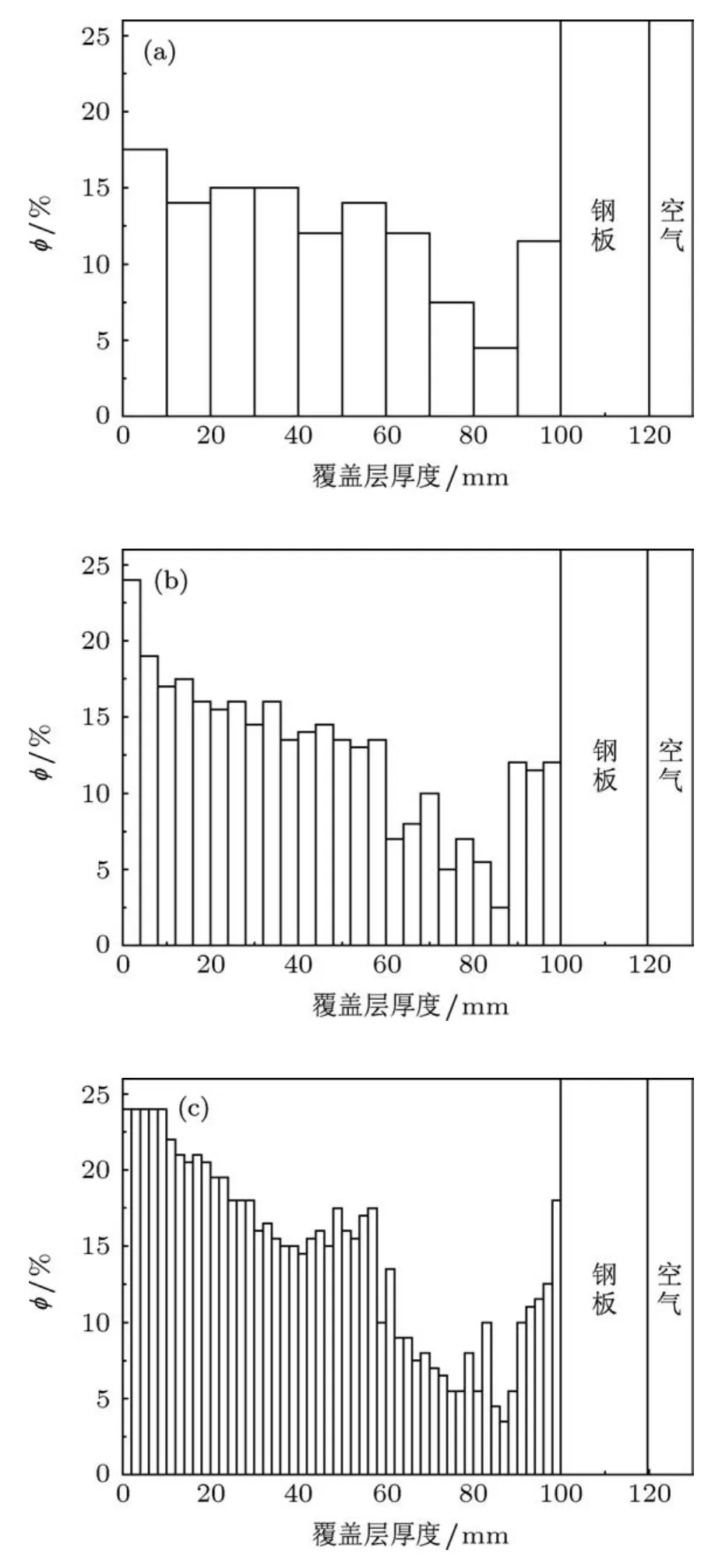
图5 不同层数(N)的多层优化结构的玻璃微球体积含量φ在覆盖层厚度方向上的分布 (a)N=10;(b)N=25;(c)N=50

定义吸声系数α=0.7对应的最小频率为低频截止频率 fc.优化的目标是在满足 f＞fc,α≥0.7的前提下,使 fc尽可能小.将吸声覆盖层在厚度方向上分别等分成10,25,50层进行了优化.优化后φ在厚度方向上的分布如图5所示,三种优化结构的平均玻璃微球体积含量分别为12.3%,12.72%,14.44%.虽然分层不同,但是φ的分布有一定的相同点：由内向外φ先减小,然后逐步增加,增加的过程中有起伏.虽然给定了φ从0到30%的61种复合材料,但是优化算法只选择了φ从2.5%到24%之间的复合材料.三种不同分层的优化结构的吸声系数谱图如图6(a)所示,吸声系数的截止频率 fc分别为2490,2580和2670 Hz,分层越多,fc越小.当 f＞fc,三种优化结构的吸声系数均大于0.7.分层越多,越有利于提高覆盖层的低频吸声性能,但是对制备工艺的要求会更高.

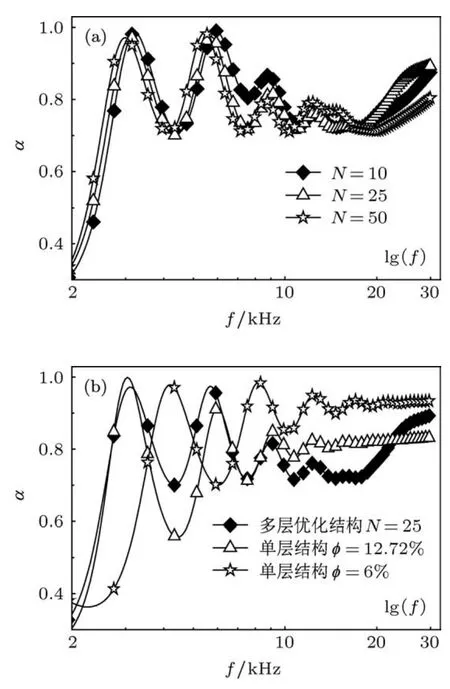
图6 (a)不同层数的多层优化结构的吸声系数谱图;(b)多层优化结构(N=25)与单层结构(φ=12.72%和φ=6%)的吸声系数谱图

将多层优化结构(N=25)覆盖层的吸声性能与玻璃微球体积含量φ=12.72%和φ=6%的单层结构覆盖层做了比较.如图6(b)所示,多层优化结构和单层结构(φ=12.72%)的截止频率 fc相同,均为2580 Hz.尽管多层优化结构的高频吸声系数相对较弱,但是单层结构(φ=12.72%)在4050—5230 Hz之间的α小于0.7,最小值为0.56.φ=6%是单层结构满足 f＞fc,α≥0.7的前提下,复合材料中的最大玻璃微球体积含量.虽然单层结构(φ=6%)在 f＞6730 Hz的频带范围的吸声性能优于多层优化结构,但是其低频截止频率 fc为3440 Hz,比多层优化结构高出了860 Hz.

将多层优化结构(N=25)覆盖层的玻璃微球体积含量φ在厚度方向上进行有序分布,形成两种多层结构覆盖层,如图7(a),(b)所示.多层结构图7(a)的玻璃微球体积含量φ在厚度方向上由内向外增加;而多层结构图7(b)的φ由内向外减小.如图8所示,对比了多层优化结构与多层结构的吸声系数频谱.尽管多层结构(a)在高频的吸声性能优于多层优化结构,但是其低频截止频率 fc为2750 Hz,比多层优化结构高出170 Hz,而且在4300—5300 Hz之间的α小于0.7.多层结构(b)除了在3100—3500 Hz的吸声系数α略大于多层优化结构,其他频带的α均小于多层优化结构.

通过以上的对比分析可以看出,相对于单层结构和有序分布的多层结构,多层优化结构的低频截止频率较低,低频的吸声系数峰值之间的谷值较高.虽然高频的吸声系数较低,但是仍然大于0.7.

图7 多层结构(a)和(b)的玻璃微球体积含量在厚度方向的分布

由(15),(16)式可以看出,覆盖层的表面声阻抗和水的声阻抗匹配越好,反射吸声越小,吸声系数越大.水的特性声阻抗近似为实数(ρ0c0=1.5×106kg·m-2·s-1),因此表面的声阻抗的实部Zr1要尽可能接近水的特性声阻抗,而虚部尽快接近0.对比了多层优化结构(N=25)、多层结构(a)和单层结构(φ=12.72%)覆盖层在4000—6000 Hz之间的表面声阻抗.如图9(a)所示,尽管三种结构的覆盖层的Zr1均小于水的特性声阻抗,但是多层结构在4500—5700 Hz之间的Zr1较大.如图9(b)所示,对比三种结构的覆盖层的Zm1,多层结构在4300—5800 Hz之间的Zm1曲线更接近Zm1=0.因此,多层优化结构覆盖层在低频的吸声系数峰值之间的谷值较高.

图8 多层优化结构(N=25)与多层结构(a),(b)的吸声系数谱图对比

图9 多层优化结构(N=25)与多层结构(a),单层结构(φ=12.72%)的覆盖层的表面声阻抗谱图 (a)实部;(b)虚部

4 多层优化结构吸声覆盖层的制备工艺分析

根据目前橡胶行业的技术条件,制备黏弹性复合材料的多层优化结构并不复杂,其制备工艺可以分为：

1)将一定体积的玻璃微球粉末与黏弹性聚合物生胶混炼,使得玻璃微球在聚合物中分散均匀,并按照设计要求,制备出不同玻璃微球体积含量的生胶;

2)将工序1)生成的不同玻璃微球体积含量的生胶,按照设计尺寸,压延成一定面积和厚度的生胶片;

3)将工序2)生成的生胶片按照优化的厚度分布叠在一起,生胶片有一定的黏性,各层胶片会自然粘贴到一起;

4)将工序3)生成的多层生胶片进行硫化,便可以生成多层优化结构的黏弹性复合材料覆盖层.

日常生活中常见的汽车轮胎就是一种黏弹性聚合物复合材料的多层结构,多层优化结构的黏弹性复合材料覆盖层的制备可以借鉴轮胎的制造工艺.

5 结论

玻璃微球的引入可以提高黏弹性复合材料的机械阻尼,影响黏弹性复合材料的力学和声学性能.增加玻璃微球体积含量可以使复合材料覆盖层的低频吸声系数的峰值移向更低频率,但是高频的吸声系数会降低.采用遗传算法对玻璃微球体积含量在覆盖层厚度方向上的分布进行优化,可以在保证覆盖层的高频吸声系数大于某一限值(例如0.7)的条件下,尽可以能提高其低频吸声性能.含玻璃微球的黏弹性复合材料多层优化结构覆盖层中不含有宏观的腔体,其耐压性能有保证.另外,其结构简单,对制备工艺的要求不高.本文形成的理论方法可以实用于水下吸声覆盖层的设计.

[1]He Z Y,Wang M 1996 Appl.Acoust.9 12(in Chinese)[何祚镛,王曼1996应用声学9 12]

[2]Ma L L,Wang R Q 2006 Tech.Acoust.25 175(in Chinese)[马黎黎,王仁乾2006声学技术25 175]

[3]Ivansson S M,2006 J.Acoust.Soc.Am.119 3558

[4]Zhao H G,Liu Y Z,Wen J H,Yu D L,Wen X S 2007 Phys.Lett.A 367 224

[5]Chen H Y,Luo X D,Ma H R 2007 Phys.Rev.B 75 024306

[6]Ivansson S M 2008 J.Acoust.Soc.Am.124 1974

[7]Zhao H G,Liu Y Y,Wen J H,Yu D L,Wen X S 2007 Acta Phys.Sin.56 4700(in Chinese)[赵宏刚,刘耀宗,温激鸿,郁殿龙,温熙森2007物理学报56 470]

[8]Jiang H,Zhang M L,Wang Y R,Hu Y P,Lan D,Wei B C 2009 Chin.Phys.Lett.26 106202

[9]Zhang J M,Chang W,Varadan V K,Varadan V V 2001 Smart Mater.Struct.10 414

[10]Philip B,Abraham J K,Varadan V K,Natarajan V,Jayakumari V G 2004 Smart Mater.Struct.13 N99

[11]Yu L G,Li Z H,Ma L L 2012 Acta Phys.Sin.61 024301(in Chinese)[于利刚,李朝晖,马黎黎2012物理学报61 024301]

[12]Wang X L 2007 J.Acoust.Soc.Am.122 2626