关于线性阻尼振子第一积分的研究
2013-09-25丁光涛
丁光涛
1 引言
振动是自然界和工程技术领域中最常见的运动形式,是力学和物理学中一个基本的研究领域.经过对振动系统的理想化抽象,系统的振动规律常常以微分方程来描述,因此,求振动微分方程的积分,就是振动理论的重要课题.最简单的振动系统是简谐振子,对多维简谐振子系统的积分问题,特别是与时间无关的积分问题仍然受到重视[1-4].近来,我们引入基本积分概念,以及利用基本积分构造其他积分的方法,比较好地解决了简谐振子的第一积分构造问题,证明对n维简谐振子系统总是存在2n-1个独立的不含时的第一积分[5].由于在周围环境和工程实际中耗散因素普遍存在,故阻尼振子问题,特别是线性阻尼振子问题不仅在经典力学中长期受到关注,而且从20世纪30年代以来,也成为量子理论的重要研究课题[6-9].
本文研究线性阻尼振子系统的积分问题,利用引入线性阻尼振子的基本积分的概念,去构造多种形式的线性阻尼振子第一积分.首先,我们导出一维线性阻尼振子系统的基本积分,并利用它们来构造其他第一积分,特别是具有明显物理意义的积分和不含时间的积分,并指出线性阻尼振子与简谐振子之间的一个重要的区别;其次,将这种概念和方法推广到多维系统,重点是构造不同类型的二维线性阻尼振子系统的第一积分,提出利用不同自由度的基本积分构造其他积分的方法;给出n维情况的一般结果,证明对n维线性阻尼振子系统也存在2n-1个独立的不含时的第一积分;最后,利用变量变换将一维线性阻尼振子的第一积分变换成简谐振子的形式,并讨论了n维系统的一般情况,即将n维线性阻尼振子问题变换成n维简谐振子问题.
2 从线性阻尼振子的基本积分构造第一积分
一维线性阻尼振子的运动微分方程为
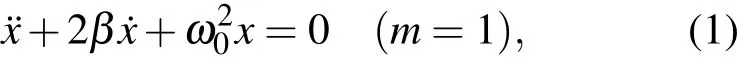
方程的两个第一积分为
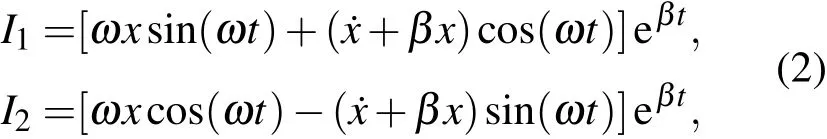
式中

将初始条件代入,即可知道I1和I2分别与初位置和初速度直接相关,它们是两个独立的积分,我们将这两个积分称为基本积分.由两个基本积分可以直接得出方程(1)的解
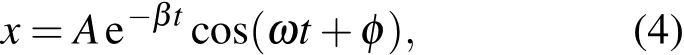
而且利用它们能够构造其他的积分.例如,
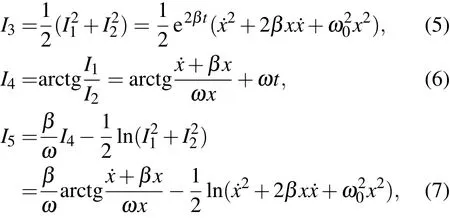
积分I3和I4分别与能量和初位相相关,而I5是不含时间的积分.应当指出,积分I5的存在是线性阻尼振子与简谐振子之间的一个重要区别,在简谐振子中不含时积分是能量积分,而线性阻尼振子能量积分(5)是含时的耗散的,但是,由于积分(5)和(6)中,都含时间,因此,利用它们也可以消去时间,得到了新的不含时积分(7),原则上这个积分给出了线性阻尼振子的相轨道.当阻尼不存在,即β=0时,该积分与能量积分等价.
3 多维线性阻尼振子的第一积分
3.1 二维对称线性阻尼振子
将上述一维情况推广到二维情况.首先讨论二维对称线性阻尼振子,其运动方程为
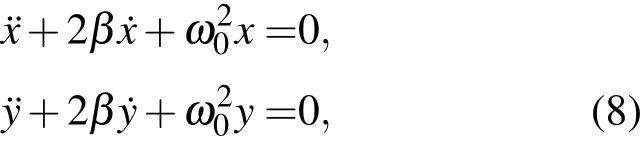
方程的四个独立的基本积分为
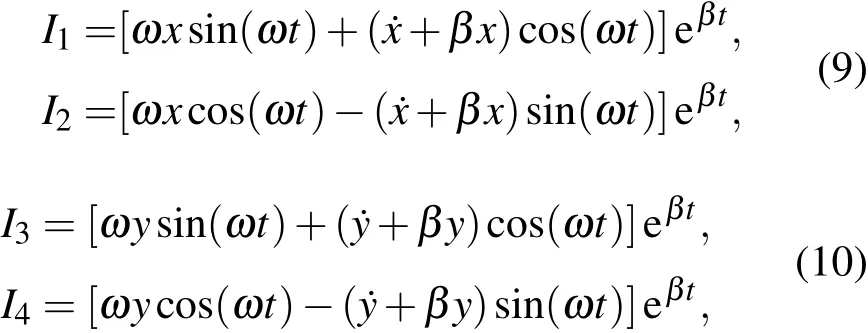
这四个独立的积分的物理意义清楚,利用它们同样能够导出二维线性阻尼振子的解,也能利用它们构造二维线性阻尼振子其他的积分.例如,与两个分振动对应的四个积分
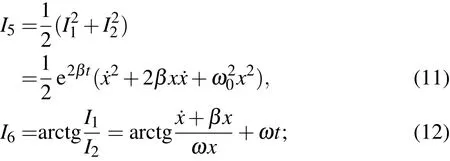
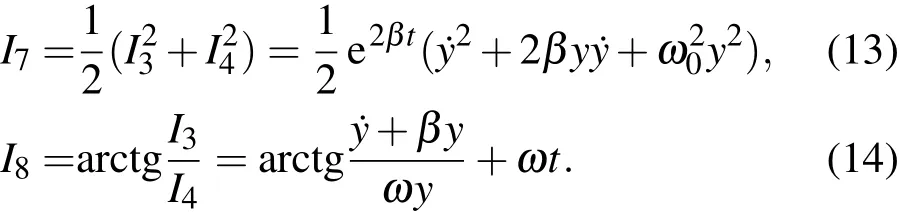
这些积分的物理意义也很明确,直接利用它们还可以得到其他积分,例如
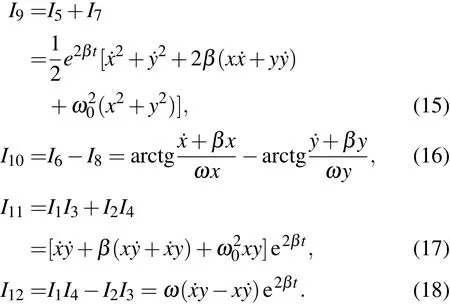
对于二维对称线性阻尼振子而言,这四个积分也是重要的积分.值得注意的是I10是与时间无关的积分.由于(9)和(10)式中四个第一积分的任意函数都是积分,故二维对称线性阻尼振子的积分有任意多个,其中大部分是含时的.但是,在讨论系统运动时,人们往往更重视寻找与时间无关的积分,如(16)式中的积分,这样的积分代表着相空间中一个不随时间变化的曲面,系统相点在其上运动.对二维系统,如果能够导出3个独立的与时间无关的第一积分,那么就确定了系统的相轨道.对于二维对称线性阻尼振子系统与时间无关的积分可以如下方法来构造,例如
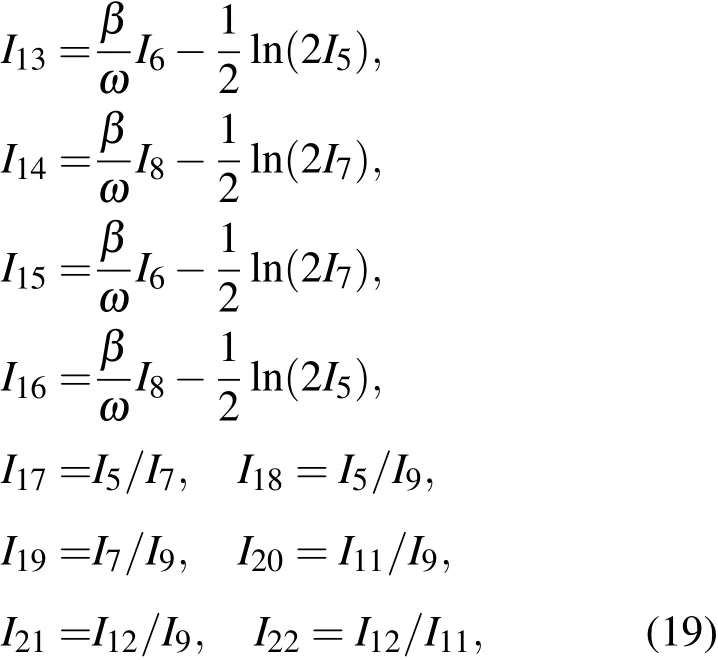
等等.这些积分中I13,I14是与(7)式中积分同一个类型的,I15,I16也是这种类型的积分,但是涉及两个自由度.这些与时间无关的积分中独立的只有3个,例如,可选择I10,I13,I14作为一组独立的积分.大多数积分之间是函数相关的,例如
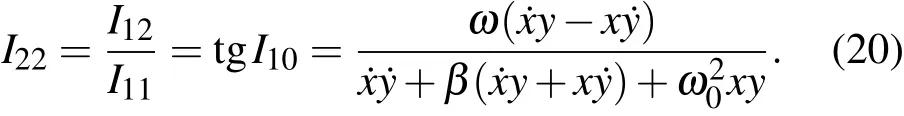
上述结果表明,导出了全部基本积分就解决了构造二维对称线性阻尼振子系统第一积分问题,证明了这种系统存在三个独立的不含时的第一积分.
3.2 二维非对称线性阻尼振子
对于二维非对称线性阻尼振子,运动方程为
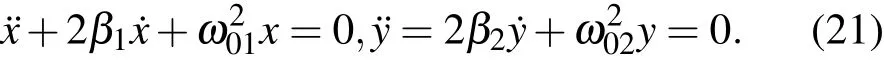
对于每一个分振动,(9)和(10)式形式的基本积分,以及(11)—(14)式类型的积分都存在,即
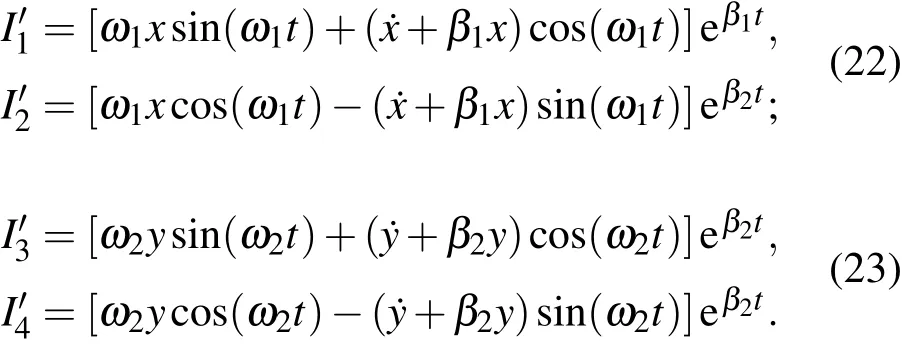
式中
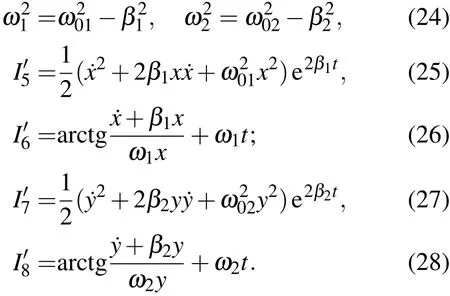
比较容易得到的涉及整个系统的积分为
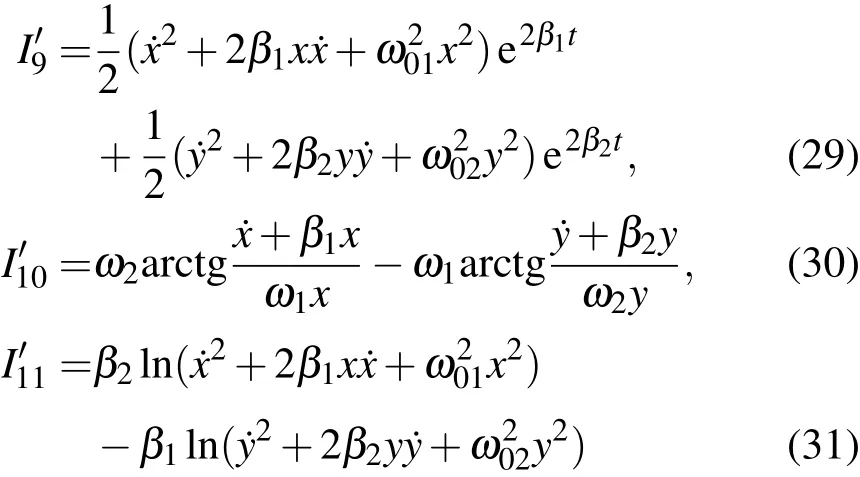
等等,其中I1′0,I1′1是不含时间的积分,当然,还可以构造其他的涉及和不涉及整个系统的积分,包括含时间的和不含时间的积分,例如,对每一个分振动都可以导出(7)式类型的与时间无关的积分.值得注意的是,导出这些积分与两个分振动的频率之比是有理数还是无理数无关.对二维非对称的线性阻尼振子三个独立的不含时第一积分,可以选择对应着两个自由度的(7)式类型的积分,再从(30)和(31)式中任意选择一个积分.综上所述,我们利用直接构造方法证明了不同类型的二维线性阻尼振子总是存在三个独立的不含时第一积分.还应当指出,与一维情况相似,由于线性阻尼振子基本积分中存在两个与时间相关的因子,故不论是一维情况,还是二维情况,线性阻尼振子比简谐振子多一种消去时间的方法,如积分I7,I13,I15I′11等.
3.3 n维线性阻尼振子
在上述一维二维线性阻尼振子从基本积分构造其他积分的基础上,进一步讨论n维系统独立的不含时积分的构造问题.设系统运动微分方程为
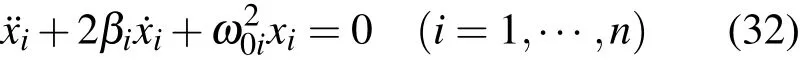
系统的2n个基本积分是
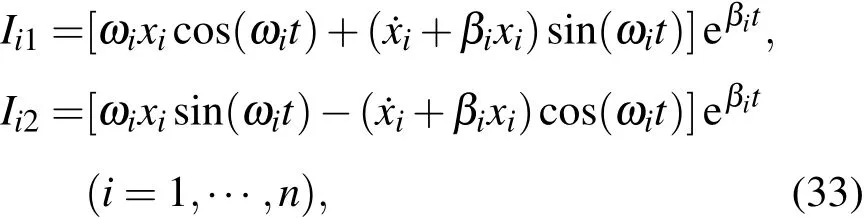
式中

我们利用直接构造法证明系统存在2n-1个独立的不含时的第一积分.首先,对每一个自由度都可以构造如下的第一积分
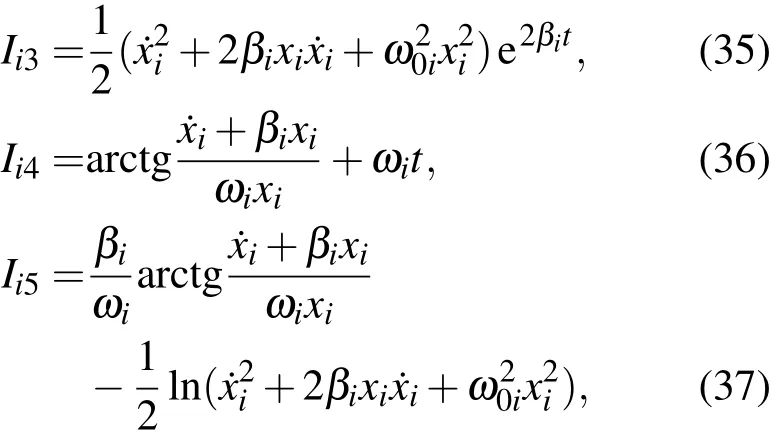
显然,(37)式中n个不含时第一积分是独立的.其次,利用不同的自由度的基本积分构造其余n-1个不含时第一积分.为了讨论简明有序,我们选取第一个自由度为基准,假设存在m个自由度的振动的参数βk和ωk(k=1,···,m)相同,其余的 n-m个自由度振动参数 βj和 ωj(j=m+1,···,n)与第一个自由度振动参数β1和ω1不同(至少有一个参数不同).由前m个自由度可以构造m-1个不含时积分
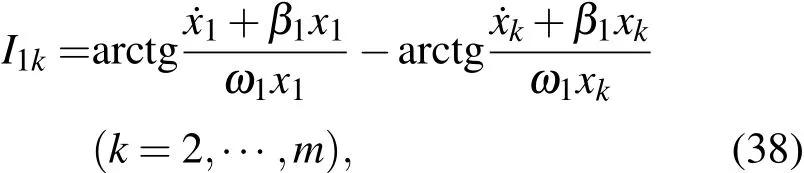
利用后面n-m个自由度可以构造n-m个不含时积分
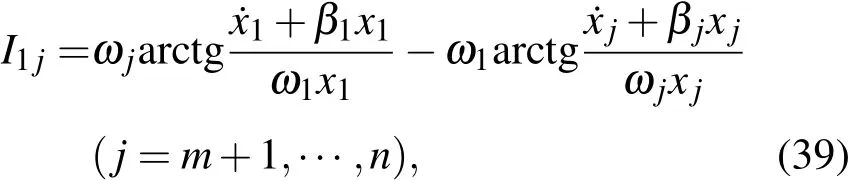
(38)和(39)式中n-1个积分也是独立的,还应当指出,它们实际上可以统一地写成(39)式的形式.(37)—(39)式中2n-1个积分构成了n维线性阻尼振子系统一组独立的不含时的第一积分.当然,还可以利用其他函数形式的不含时积分构成2n-1个独立的积分,例如,根据情况可以将上述积分中的某些积分代以(17),(18)或(31)式类型的积分.
4 从线性阻尼振子到简谐振子的变换
经典力学中简谐振子系统是非常重要的系统,其运动规律研究得十分深入;量子力学中情况也类似,简谐振子的量子化是一个完全解决的问题[1,2,4].然而,从数学表示上来看,简谐振子与线性阻尼振子之间不是绝然分开的,它们之间可以相互变换.利用变量变换方法能够将线性阻尼振子的微分方程和第一积分变换成为简谐振子形式的,这个变换将利于对线性阻尼振子问题的研究,根据前面得到的结果,我们需要对基本积分完成这样的变换.
首先研究一维情况,引入与时间相关的变换

方程(1)可以写成如下等效的简谐振子的形式
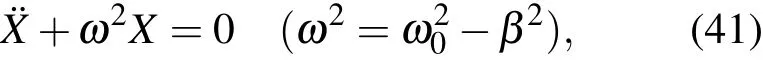
(2)式中两个积分变换成
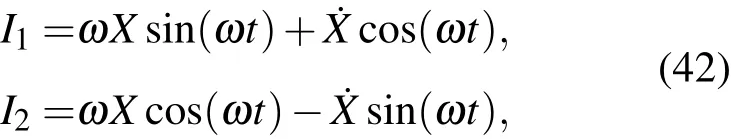
这正是简谐振子的第一积分.显然,通过变换(40)式的逆变换,(42)式中两个积分仍变换为(2)式中的两个积分.
上述变换可以直接推广到多维情况,对n维线性阻尼振子(32)式,引入变换
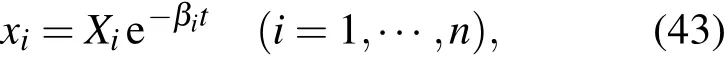
则方程(32)和对应的2n个基本积分都变换成简谐振子形式的,即
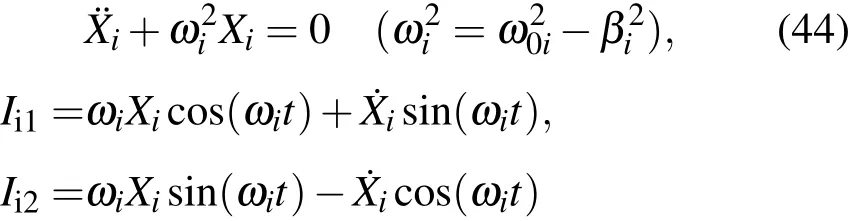

利用变换(43)式的逆变换从(45)式中2n个简谐振子形式的积分就得到(33)式中2n个线性阻尼振子的基本积分;由简谐振子基本积分构成的其他积分也逆变换成为线性阻尼振子的对应积分.然而,必须指出的是,线性阻尼振子的基本积分(33)式可以通过变换(43)式得到简谐振子基本积分(45)式,由基本积分构成的积分(35)和(36)式也可以直接变换成简谐振子的对应积分.但是,(37)式类型的线性阻尼振子积分直接利用变换(43)式得到的结果,必须经过进一步变换才能成为简谐振子形式的积分.将(43)式代入(37)式得到
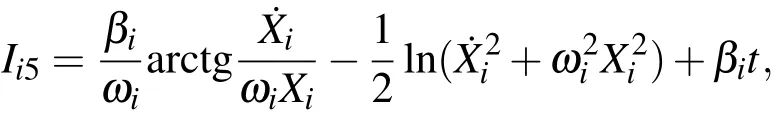
上式不能称为简谐振子形式的积分.但是,利用积分(36)式,可以导出
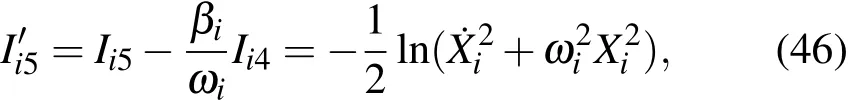
这种积分与简谐振子的能量积分等价.这种情况的出现,与我们前面指出的由于线性阻尼振子基本积分中存在两种与时间相关的因子,故线性阻尼振子情况比简谐振子情况多一种消去时间的方法相关;这就是说,由于阻尼因素的存在,从物理本质上线性阻尼振子与简谐振子之间存在着区别.
5 结论
1)本文以新的思路对线性阻尼振子系统第一积分进行深入的研究,即导出直接与初始条件相关的基本积分后,再利用它们构造线性阻尼振子的其他第一积分,包括不显含时间的第一积分.这种处理方法可以应用于一维系统和多维系统,包括对称和非对称系统.
2)通过直接构造法证明,二维线性阻尼振子系统,无论是对称的还是非对称的,都存在并可以实际构造出三个不显含时间的第一积分;n维线性阻尼振子系统存在2n-1个独立的不显含时间的第一积分.
3)通过变量变换,将线性阻尼振子方程和第一积分变换成简谐振子形式的,这样就使得处理线性阻尼振子的问题,包括经典力学和量子力学问题,得到简化.研究表明,对简谐振子的第一积分能够利用变量变换直接变成对应的线性阻尼振子的结果,但是,有些线性阻尼振子的第一积分利用变量变换导出对应的简谐振子的结果时,需要利用其他第一积分.
[1]Goldstein H,Poole C,Salko J 2005 Classical Mechanics(3rd Ed.)(Beijing:Higher Education Press)
[2]Li D M,Cheng C M 2006 Classical Mechanics(Beijing:Higher Education Press)(in Chinese)[李德明,陈昌民2006经典力学(北京:高等教育出版社)]
[3]Lou Z M,Mei F X 2012 Acta Phys.Sin.61 110201(in Chinese)[楼智美,梅凤翔2012物理学报61 110201]
[4]Zeng J Y 2001 Quantum Mechanics(Beijing:Science Press)(in Chinese)[曾谨言2001量子力学(北京:科学出版社)]
[5]Dekker H 1981 Phys.Rep.80 1
[6]Um C I,Yean K H,George T F 2002 Phys.Rep.362 63
[7]Pen H W 1980 Acta Phys.Sin.29 1084(in Chinese)[彭桓武1980物理学报29 1084]
[8]Zhu R Z 1981 Acta Phys.Sin.30 1410(in Chinese)[朱如曾1981物理学报30 1410]
[9]Ling R L,Feng J F 1998 Acta Phys.Sin.47 1952(in Chinese)[凌瑞良,冯金福1998物理学报47 1952]
