脉冲星信号的经验模态分解模态单元比例萎缩消噪算法*

王文波 张晓东 汪祥莉

1 引言

脉冲星是一种高密度、高速自转且具有强磁场的中子星,其最重要的特征是自转具有超高的稳定性和均匀性,其毫秒级的脉冲辐射周期被称为是自然界中最稳定的时钟[1].近年来,脉冲星在计时、定位、导航、电波传播学和天体物理学等多个领域日益展现出巨大的应用潜力,受到越来越广泛的关注和研究[2-4].然而,由于脉冲星在距离地球上千甚至几十万光年的遥远深空中,其辐射脉冲信号在传播和接收过程中不可避免地受到空间介质、宇宙辐射、大气层色散延迟以及地球运动等众多因素的影响,导致所接收到的脉冲辐射信号极弱且常常淹没在噪声之中[5,6].因此,对脉冲辐射信号中的噪声进行有效滤除将直接影响到脉冲累积轮廓和脉冲到达时间的计算精度,是脉冲星信号后继研究、应用最根本的前提和基础.

小波分析由于具有良好的时频局域化特性、多分辨率、去相关性等特点,被广泛应用于脉冲星信号的消噪中,取得了较好的消噪效果[7,8].但在应用小波方法消噪时,需要预先选定小波基和分解层数,相同条件下选用不同的小波基和分解层数,对去噪结果影响很大,特别是小波基函数的选择,对去噪结果有决定性的影响.而如何选择小波基和最优分解层数是小波分解中一个很难解决的问题,这给利用小波进行信号去噪带来了很大的不便[9,10].经验模态分解(empiricalmodedecomposition,EMD)是一种新的完全数据驱动的自适应信号分解算法[11],可以把数据分解成具有物理意义的一组内蕴模态函数(intrinsic mode function,IMF)分量.EMD在分解信号时,不需要预先确定基底和分解层数,而是根据信号自身特性,自适应地确定基底和最优分解层数.对于非线性和非平稳信号,EMD的分解结果比小波分解结果更清晰、准确[12,13],分解出的IMFs能够充分保留信号本身所固有的非线性和非平稳特征.

对于非线性和非平稳信号,EMD消噪可以获得比小波消噪更好的效果[14-17],脉冲星信号是典型的非平稳信号[18],本文将EMD应用于脉冲星信号的消噪中.利用EMD对非线性、非平稳信号消噪已得到了较多的研究.Boudraa和Cexus[15]提出了部分重构的EMD消噪算法,但部分重构消噪算法中将前几项IMF当作噪声项直接删除,丢失了较多的细节信息而且噪声不能被有效去除.Olufemi等[16]提出了基于系数阈值的EMD消噪算法,但基于系数阈值的消噪算法破坏了IMF中模态单元的完整性,影响了去噪的效果.文献[17,19]提出了基于模态单元阈值的EMD消噪算法,将IMF中两个过零点间的波动单元-模态单元作为一个整体,以模态单元作为基本单位,利用阈值方法进行去噪,保持了IMF中模态单元的完整性,有效提高了去噪效果.但该算法中对极值小于阈值的模态单元直接删除,不考虑其中所包含的细节信息;对于极值大于阈值的模态单元直接保留,不考虑其中所包含的噪声,势必导致部分信号细节信息被误删且噪声不能被完整去除,影响了去噪效果的进一步提高.本文在EMD模态单元阈值去噪算法的基础上,提出了一种基于模态单元比例萎缩的EMD去噪方法,并应用于脉冲星信号的消噪处理.所提出的方法中以模态单元为基本单位构造最优比例萎缩因子,对IMF中的每个模态单元都进行比例萎缩去噪,在保持模态单元完整性的基础上,有效去除每个模态单元中所含的噪声.分别采用小波硬阈值去噪、比例萎缩小波去噪、EMD模态单元阈值去噪和本文方法对脉冲星信号进行消噪对比实验,结果表明本文方法在噪声去除和信号细节特征保持两方面都有较好的提高.

2 基于模态单元比例萎缩的EMD去噪模型

EMD的主要目的是将待分析信号分解为一系列表征时间尺度的IMF分量,要求IMF分量必须满足两个条件：IMF的极值点个数与过零点个数不超过1;由极大值点和极小值点确定的包络线均值为零.EMD分解结束后,原始信号x(t)可被表示为一组IMF和一个余项之和：

其中imfk表示第k个IMF分量,rK(t)表示余项,K表示分解出的IMF的总层数.每个IMF的极大、极小值点形成的上、下包络线关于时间轴局部对称,反映了信号内部的固有波动特性.

在IMF中,一次完整的波动由三个过零点和一个波峰、一个波谷构成,相邻的两个过零点之间只有一个极值点.由两个过零点和一个极值点所构成的信号部分是IMF最基本的组成单元,它是构成信号固有波动的最小完整单元,一般将其称为IMF的模态单元[16],模态单元中极值点的系数绝对值称为模态振幅.对于第k层内蕴模态函数imfk,如果把imfk中的第i个模态单元记为z(k)i,则imfk可被表示为其中 k=1,2,···,K,本文中模态单元的模态振幅记为,的极值点记为.

在基于系数阈值的EMD去噪算法中[19],借鉴小波阈值去噪的思想构造imfk的去噪阈值Tk,然后利用该阈值对imfk系数进行处理.若令hk(t)=imfk(t),基于IMF系数的硬阈值去噪算法可表示为

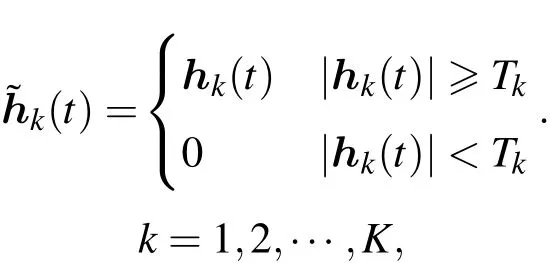
在基于IMF系数的阈值去噪算法中,IMF中所有小于阈值的系数都被置0,导致模态振幅较大的模态单元中的部分点也被置零(如图1(c)所示),破坏了模态单元局部固有波动的完整性,影响了去噪的效果.

基于模态单元阈值的EMD去噪算法中[16,20],将模态单元作为基本单位,针对模态单元构造阈值Tk,利用Tk对imfk中的模态单元进行阈值处理.基于模态单元的阈值去噪法可表示为

可以看出在该算法中,模态振幅小于阈值的模态单元被置零,而模态振幅大于阈值的模态单元被完整保留(如图1(d)所示),没有破坏IMF中模态单元局部固有波动的完整性,较好地提高了EMD的去噪效果.

但文献[10,17]的研究表明,imfk的每个部分都分布有不同程度的噪声：模态振幅较大的模态单元主要由信号的波动构成,但仍含有少量噪声,直接保留会导致噪声不能完整去除;而模态振幅较小的模态单元虽然主要由噪声的波动构成,但仍含有部分信号细节信息,直接置零将不可避免地会损失部分信号细节.为了进一步提高EMD的去噪效果,本文借鉴小波比例萎缩去噪的思想,以模态单元为基本单位,构造合适的比例萎缩因子,对IMF中的每个模态单元进行比例萎缩去噪.

假设hk=imfk=中模态单元zik的比例萎缩因子为θik,则基于模态单元的比例萎缩去噪方法可表示为

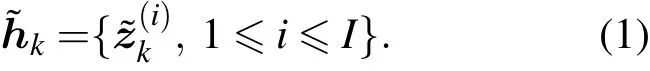
基于模态单元比例萎缩的去噪算法没有破坏模态单元局部固有波动的完整性,而且对振幅较大的模态单元和振幅较小的模态单元都进行了相应的萎缩去噪处理(如图1(e)所示),在一定程度上改善了模态单元阈值去噪算法的不足,可以更好地去除噪声并保留信号细节信息.信号经EMD模态单元比例萎缩去噪后可表示为

式中,Kd表示需要滤波的IMF数目,对于高斯白噪声,通常取Kd=min(8,K),即去噪时仅对前8个IMF进行滤波,而其余的IMF直接保留.在基于模态单元的比例萎缩去噪中,构造合适的模态单元比例萎缩因子θki非常关键.若想构造合适的比例萎缩因子,最大程度的恢复原始信号,必须了解IMF的统计模型.本文在下一节中对含噪脉冲星信号IMF的统计特性进行讨论.

图1 EMD去噪算法模型 (a)测试信号Doppler第4层IMF(imf4);(b)imf4中所选部分放大图;(c)系数阈值去噪;(d)模态单元阈值去噪;(e)模态单元比例萎缩去噪

3 含噪脉冲星信号IMF的统计特性分析

3.1 含噪脉冲星信号IMF中噪声分布形式

含噪脉冲星辐射信号y经消色散处理后,可以近似看作是有用信号与高斯白噪声混合组成,即

式中,x为有用脉冲星信号,d为服从正态分布的高斯白噪声.含加性高斯白噪声的信号经EMD分解后,IMF中噪声的分布形态尚没有完善的理论体系,但通过大量的实验分析,一般认为IMF中的噪声仍服从加性分布[13,21].因此,脉冲星辐射信号经EMD分解后,第k层内蕴模态函数hk=imfk可设为

其中sk表示imfk中所含的信号信息,nk表示所含噪声,且sk和nk相互独立.

3.2 含噪脉冲星信号IMF中信号项和噪声项的统计模型

为了对imfk中的模态单元构造最优比例萎缩因子,需要知道信号项sk和噪声项nk的分布形式.纯零均值高斯白噪声经EMD分解后,其IMF系数仍服从零均值正态分布[17],即

式中σ2k,n为nk的方差.但imfk中信号项部分sk的分布形式尚没有具体的研究结果,本文通过实验的方式分析sk的统计特性.由于EMD分解后IMF中信号和噪声混杂在一起,难以直接对信号项的统计特性进行分析,本文从含噪脉冲星信号的IMF系数hk出发,对信号项sk的统计特性进行间接分析.

在脉冲星信号B1953+29的标准轮廓中添加白噪声后进行50次EMD分解,取50次分解结果的平均值作为最终结果,统计各层IMF的系数分布,并与高斯分布进行比较.图2给出了含噪脉冲星信号第2—5层IMF系数的直方图和相应的高斯分布模拟逼近曲线,直观上可以看出高斯分布可以较好地逼近IMF系数的分布.为了进一步验证零均值高斯分布对含噪脉冲星信号IMF系数的逼近程度,对IMF的系数分布进行偏度、峰度检验[22].偏度、峰度检验法是正态性检验的经典方法,随机变量S的偏度v1和峰度v2是指S的标准变化量[S-E(S)]/的三阶和四阶矩,即

其中,E(S)和D(S)分别表示S的期望和方差.当随机变量S服从正态分布时,v1=0且v2=3.设S1,S2,···,Sn是来自总体S的样本,则样本偏度v1和样本峰度v2可由下式进行简单计算：v1=B3/B,v2=B4/B22,式中Bk(k=2,3,4)表示样本的k阶中心矩.

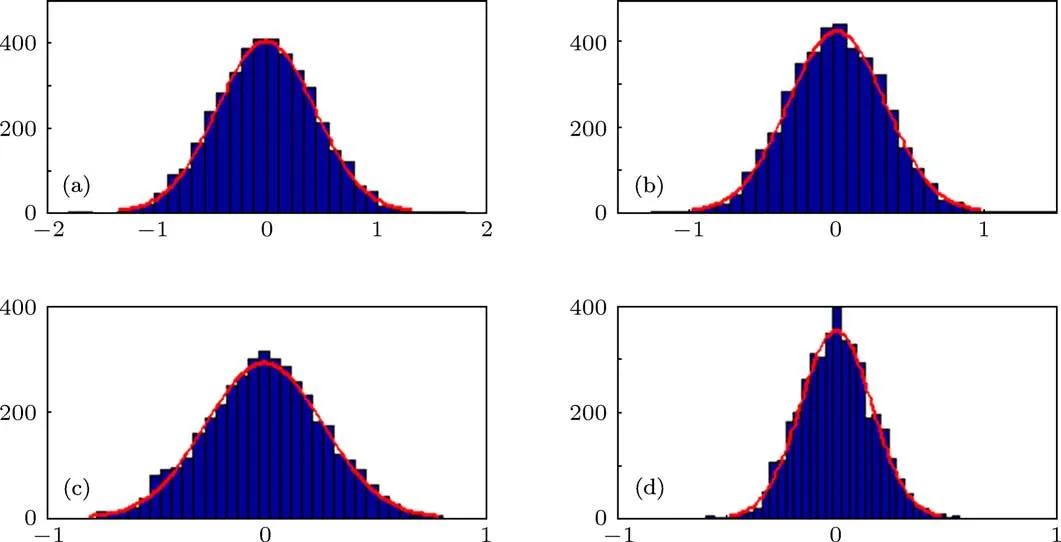
图2 含噪脉冲星信号IMF系数的高斯逼近 (a)imf2系数直方图及高斯逼近;(b)imf3系数直方图及高斯逼近;(c)imf4系数直方图及高斯逼近;(d)imf5系数直方图及高斯逼近

如果含噪脉冲星信号的IMF系数符合零均值高斯分布,则其样本偏度接近于0,而样本峰度接近于3,计算其第2—5层IMF的样本偏度和样本峰度,结果如表1所示.

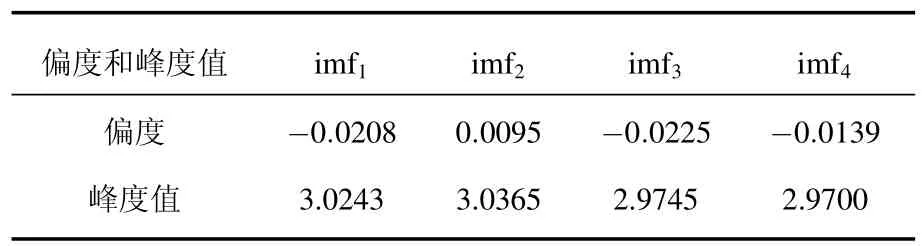
表1 含噪脉冲星信号IMF的样本偏度和峰度

从表1可以看出,含噪信号各层IMF的样本偏度和样本峰度都比较接近于0和3,样本偏度绝对值的均值约为0.0167,样本峰度的平均值约为3.0013.因此,高斯模型可以较好地模拟含噪脉冲星信号IMF系数的分布特性.本文对B2351+61和B1953+29等脉冲星信号分别添加不同强度的白噪声进行多次实验,得到了类似的实验结果,所以可假设含噪脉冲星信号的IMF系数近似服从零均值高斯分布,即hk∼N(0,σ2h,k).由于sk=hk-nk,且hk,nk都服从零均值高斯分布,由概率知识可知imfk中信号项部分sk也服从零均值高斯分布,即

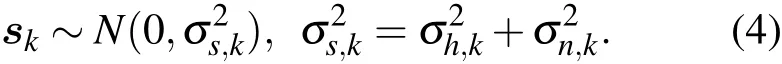
4 模态单元比例萎缩因子的确定

本文采用线性最小均方误差(linear minimum mean square error estimation,LMMSE)准则计算imfk去噪时的最优比例萎缩因子[22].令hk=imfk,由(2)式可知hk=sk+nk,设去噪时的比例萎缩因子为θk,则去噪后的信号

为了使˜hk与原始真实信号sk间的均方误差E[(sk-˜hk)2]最小,根据LMMSE理论,应有E[(sk-˜hk)hTk]=0,从而可求出

考虑到信号sk与噪声nk都服从零均值高斯分布且相互独立,所以

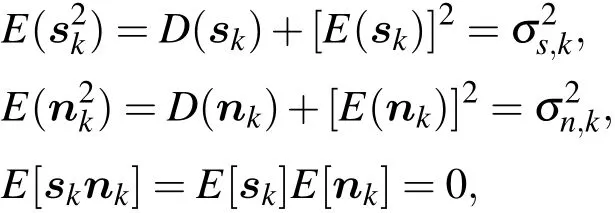
因此

但如果对imfk中的每个系数都按照自身的比例萎缩因子进行去噪,会造成一个模态单元内出现多个极值的情况,将破坏模态单元固有波动的完整性.在模态单元zik内,极值点e(ik)反映了模态单元最本质的波动特征和信息,因此可将极值点e(ik)的萎缩因子θ(e(ik))作为整个模态单元zik的萎缩因子,按此方法对imfk进行比例萎缩去噪,即

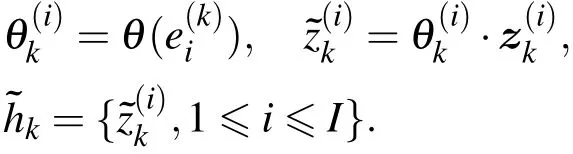
此时,由于整个模态单元zki内采用相同的萎缩因子θ(e(k)i),因此不会破坏模态单元局部固有波动的完整性.本文中噪声标准差σn,k采用(5)式进行估计,

式中HH表示hk的高频子带小波系数,而信号方差σ2s,k采用文献[24]中提出的方法进行估计,即

这里M表示所选窗口中信号的长度,本文中取M=5.

5 实验分析

本文中选用B1953+29和B2351+61脉冲星辐射信号进行实验分析,数据来源于欧洲脉冲星网络数据库EPN(the European Pulsar Network Data Archive).脉冲星信号B1953+29和B2351+61的标准轮廓如图3(a)和图4(a)所示,在标准轮廓中分别添加一定量的高斯白噪声模拟含噪脉冲星信号,B1953+29加噪后的信号如图3(b)所示,其信噪比为10;B2351+61加噪后的信号如图4(b)所示,其信噪比为20.分别采用硬阈值小波去噪法[24](wavelet hard threshold denoising,WHD)、比例萎缩小波去噪法[23](wavelet proportion shrinking denoising,WPSD)、EMD模态单元阈值去噪法(mode-cell threshold denoising,MTD)和本文提出的EMD模态单元比例萎缩去噪法(mode-cell proportion shrinking denoising,MSD)分别对含噪脉冲星信号进行消噪处理,消噪后的信号如图3(c)—(f)和图4(c)—(f)所示.对消噪结果采用以下四个参数进行联合评价[7]：信噪比、均方根误差、峰值相对误差、峰位误差.其中峰值相对误差和峰位误差的定义公式如下.

1)峰值相对误差：REPV=(Vo-Vd)/Vo·100%,式中Vo,Vd分别表示脉冲星辐射信号标准轮廓的脉冲峰值和消噪后信号的脉冲峰值.

2)峰位误差：EPP=|Po-Pd|,式中Po,Pd分别表示脉冲星辐射信号标准轮廓波的脉冲峰位值和消噪后辐射信号的脉冲峰位值.

首先从视觉效果上对四种消噪方法进行比较.从图3(c)和图4(c)可以看出,WHD算法较好地去除了脉冲星信号中的噪声,消噪后信号的平滑部分与标准轮廓基本符合,但由于对小波阈值的系数全部去除,使得在去除噪声的同时也损失了较多的细节信息,导致信号的突变部分去噪后与标准轮廓之间的符合程度较差.WPSD算法的去噪效果要优于WHD(如图3(d)和图4(d)所示),消噪后信号的平滑部分与标准轮廓符合较好,突变部分与标准轮廓的符合度有一定程度的提高.MTD的消噪效果(如图3(e)和图4(e)所示)与WPSD比较接近,在平滑部分和几个大的波峰处,两种方法去噪都取得了较好的效果,但在信号剧烈振荡的地方,MTD比WPSD具有更好的符合效果.本文方法消噪后的结果如图3(f)和图4(f)所示,通过比较可以看出,本文方法消噪后平滑部分与WPSD和MTD基本相同,但在脉冲峰值和剧烈振荡的突变点处,与标准轮廓有更好的逼近、误差更小,减小了脉冲峰高度值和位置值的偏差,突变点处的细节信息损失更小.因此从视觉分析来看,本文方法去噪效果优于WPSD和MTD,更好地保留了脉冲星信号的细节信息,在信号的突变点处与标准轮廓具有更好的吻合度.

图3 含噪脉冲星信号B1593+29消噪结果比较 (a)脉冲星信号标准轮廓;(b)含噪脉冲星信号;(c)WHD消噪;(d)WPSD消噪;(e)MTD EMD消噪;(f)本文方法消噪

表2 不同方法消噪后的参数比较

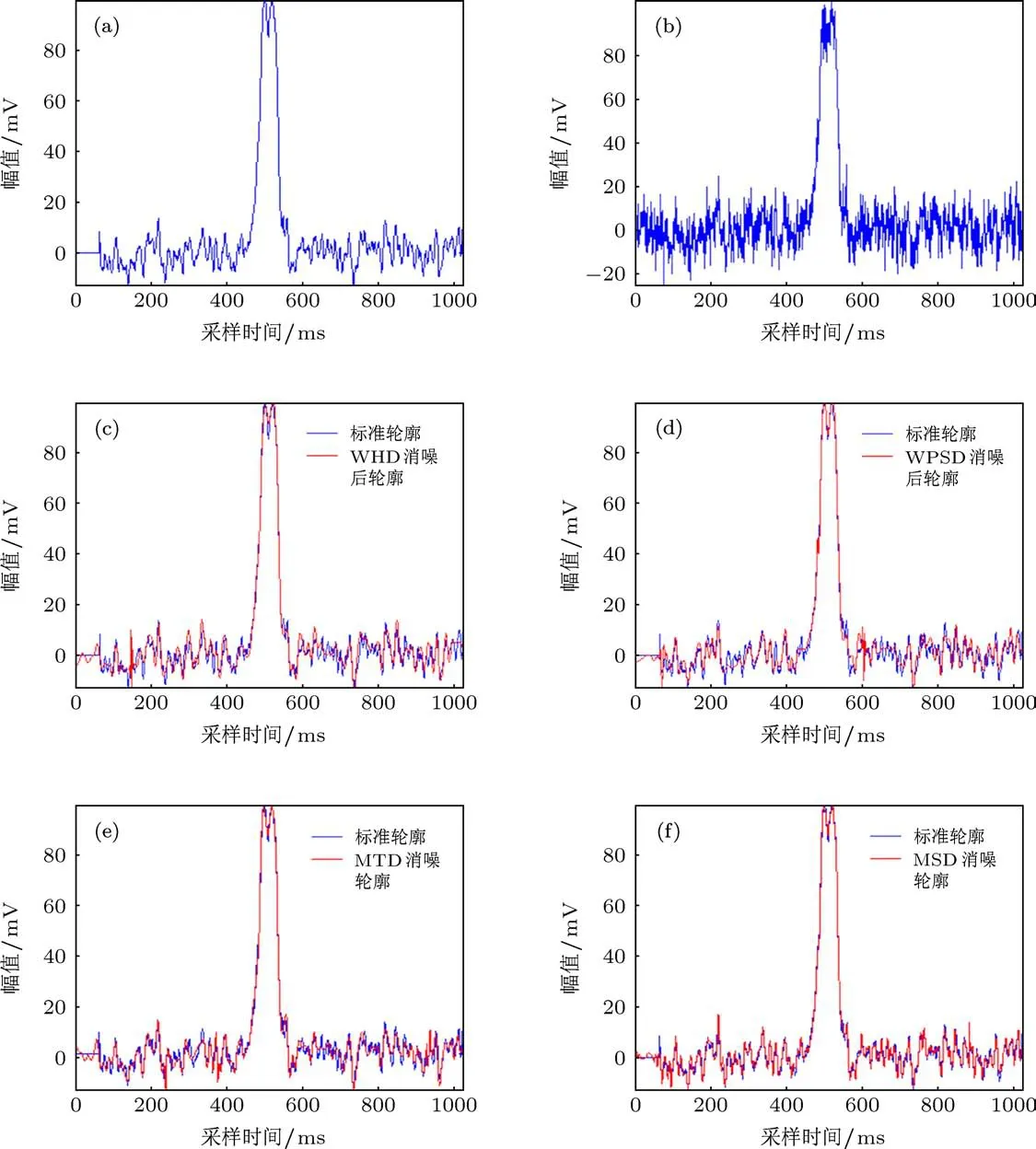
图4 含噪脉冲星信号B2351+61消噪结果比较 (a)脉冲星信号标准轮廓;(b)含噪脉冲星信号;(c)WHD消噪;(d)WPSD消噪;(e)MTD EMD消噪;(f)本文方法消噪

再对四种方法消噪后的参数进行比较,当消噪后信号的信噪比(SNR)越大,而均方根误差(RMSE),REPV和EPP越小时,表明消噪效果越好.不同方法消噪后的SNR,RMSR,REPV和EPP如表2所示.从表2可以看出,WHD的效果稍差,除了峰位误差其他三项指标都不如另外三种方法.WPSD的参数与EMD,MTD相差不大,MTD消噪后的均方根误差和峰值相对误差略优于WPSD.本文方法消噪后的脉冲星信号信噪比最大、均方根误差最小,表明本文方法消噪后的信号能更好地逼近脉冲星标准轮廓;本文方法消噪后的峰位误差与另外三种方法基本相等,但峰值相对误差小于另三种方法,表明本文方法去除噪声的同时较好地保留了信号中脉冲尖峰部分的有用细节信息,能更好地减小脉冲峰值处重要信息的损失.整体比较可知,本文方法取得了更好的消噪效果,在噪声抑制和脉冲尖峰重要信息的保持等方面都有一定程度的提高,去噪后的参数指标优于WPSD和MTD.

6 结论

将一种基于模态单元比例萎缩的EMD滤波方法应用到脉冲星信号的消噪处理中.脉冲星信号经EMD分解后,通过分析其IMF中信号项和噪声项的统计特性,以模态单元为基本单位在最小均方误差准则下构造最优比例萎缩因子,对IMF进行比例萎缩降噪.实验结果表明：与硬阈值小波消噪法、比例萎缩小波消噪法和基于模态阈值的EMD消噪法相比,本文方法能获得更好的消噪效果,可以在有效滤除噪声的同时更好地保留原信号中有用的细节信息,脉冲星信号经本文方法消噪后,具有更高的信噪比和更低的均方根误差、峰值相对误差.本文在分析脉冲星信号IMF中噪声的分布时采用的是加性噪声模型,尚缺少完善的理论证明,通过理论分析研究IMF中噪声的分布形式是今后研究的重点;本文中对IMF中信号项部分采用高斯分布进行拟合,是否可以采用其他分布如广义高斯分布、混合高斯分布等对其进行更精确的拟合逼近,也是今后将继续探讨的一个方向.

[1]Taylor J H 1991 Proc.IEEE 79 1054

[2]Xie Q,Xu L P,Zhang H,Luo N 2012 Acta Phys.Sin.61 119701(in Chinese)[谢强,许录平,张华,罗楠2012物理学报61 119701]

[3]Sheikh S I,Pines D J,Ray P S,Wood K S,Michael N L,Wolff M T 2006 J.Guidance,Control and Dynamics 29 49

[4]Zhu J,Li P Y 2008 Chin Phys.B 17 356

[5]Zhao B S,Hu H J,Sheng L Z,Yan Q R 2011 Acta Phys.Sin.60 029701(in chinese)[赵宝升,胡慧君,盛立志,鄢秋荣2011物理学报60 029701]

[6]Hu H J,Zhao B S,Sheng L Z,Yan Q R,Yang H,Chen B M 2011 Sci.Sin.Phys.Mech.&Astron.41 1015(in chinese)[胡慧君,赵宝升,盛立志,鄢秋荣,杨颢,陈宝梅2011中国科学：物理学、力学、天文学41 1015]

[7]Yan D,Xu L P,Xie Z H 2007 J.Xi’an Jiaotong Univ.41 1193(in chinese)[阎迪,徐录平,谢振华2007西安交通大学学报41 1193]

[8]Gao G R,Liu Y P,Pan Q 2012 Acta Phys.Sin.61 139701(in Chinese)[高国荣,刘艳萍,潘琼2012物理学报61 139701]

[9]Zhang H,Xu L P,Xie Q,Luo N 2011 Acta Phys.Sin.60 049701(in Chinese)[张华,许录平,谢强,罗楠2011物理学报60 049701]

[10]Li Y Q,Li P,Yan X P,Chen H M 2008 Transactions of Beijing Institute of Technology 28 723(in chinese)[李月琴,粟苹,闫晓鹏,陈慧敏2008北京理工大学学报28 723]

[11]Zhang H,Chen X H,Yang H Y 2011 OGP 46 70(in Chinese)[张华,陈小宏,杨海燕2011石油地球物理勘探46 70]

[12]Huang N E,Shen Z,Long S R,Wu M C,Shih H H,Zheng Q,Yen N C,Tung C C,Liu H H 1998 Proc.of the Royal Society of London A 454 903

[13]Flandrin P,Paulo G 2004 Int.J.Wavel.Multiresol.Inform.Proc.2 1

[14]Gao X Q,Dong W J,Gong Z Q,Zou M W 2005 Acta Phys.Sin.54 3948(in Chinese)[高新全,董文杰,龚志强,邹明玮2005物理学报54 3948]

[15]Boudraa A,Cexus J 2007 IEEE Trans.Instrum.Measur.56 2196

[16]Olufemi A,Vladimir A,Auroop R 2011 IEEE Sens.J.11 2565

[17]Kopsinis K,Mclaughlin S 2009 IEEE Trans.Signal Proc.57 1351

[18]Wu Y F,Qiu Y,Yang Y F,Ren X M 2010 Acta Phys.Sin.59 3778(in Chinese)[吴亚锋,裘炎,杨永锋,任兴民2010物理学报59 3778]

[19]Qu C S,Lu T Z,Tan Y 2010 Acta Autom.Sin.36 67(in Chinese)[曲从善,路廷镇,谭营2010自动化学报36 67]

[20]Jenet F A,Anderson S B 1998 Publica.Astrono.Soc.Pacif i c 100 1467

[21]Wu Z H,Norden E H 2004 Proc.R.Soc.Lond.A 460 1597

[22]Sheng Z,Xie S Q,Pan C Y 2006 Probability Theory and Mathematical Statistics(Beijing：Higher Education Press)p350(in Chinese)[盛骤,谢式千,潘承毅2006概率论与数理统计(北京：高等教育出版社)第350页]

[23]Chang S,Yu B,Vetterli M 2000 IEEE Ttrans.Image Proc.9 1532

[24]Marian K 2003 IEEE Signal Proc.Lett.10 324

[25]Donoho D L,Johnstone I M 1995 J.Am.Statist.Association 90 1200