储集层构型分级套合模拟方法

李宇鹏，吴胜和

（1. 中国石油大学（北京）地球科学学院；2. 油气资源与探测国家重点实验室）

0 引言

油田进入特高含水期后，河道砂体内部仍存在因隔夹层遮挡而相对富集的剩余油，且呈高度分散状态，挖潜难度大。储集层构型层次分析法（hierarchical reservoir architecture element analysis methodology）是研究复杂非均质储集层的基本方法，是预测和挖潜剩余油行之有效的分析方法。它将沉积旋回和层序地层研究、沉积体系分析、构型层次和要素分析纳为一体，以Miall的构型要素分析及储集层地质建模为核心，对非均质储集层进行系统研究[1-4]。

传统的储集层建模基于各种随机理论，以井点数据为出发点，结合其他资料对储集层进行三维表征。对于沉积相、流动单元等离散属性以及孔隙度、渗透率等连续储集层属性，地质统计学家发展、完善了各种随机建模方法[5]。目前对于储集层构型的三维模拟仍是沿用已有的离散属性的建模方法（如Sisim方法）或是应用计算机进行人工绘制[2,6-7]。虽然已有建模算法对高级别构型要素（如复合河道砂体）的三维建模有较好的效果，但难以满足砂体内部构型解剖与建模的需要；尤其对微小级次的构型单元，通过人工绘制进行三维建模的工作量巨大，效率低下。总之，对于各级构型要素的界面和各类隔夹层的分布模拟方法研究仍然落后于地质分析认识过程，必须进一步研究开发三维储集层构型的建模方法。本文基于对储集层构型研究特点和构型建模难点的分析，以曲流河储集层构型建模实践为例，介绍分级套合模拟（hierarchical nested simulation）的思路和方法。

1 储集层构型研究的特点

目前，储集层构型地质研究基本上确立了“层次约束、模式拟合与多维印证”为主的地下储集层构型表征基本思路[1]。这一思路首先突出了地质研究中的层次概念，即分级、分层次研究非均质地质体的空间分布规律。高级次单元比低级次单元具有更宏观且易辨析的规律（如亚相分布规律比微相分布规律更明确、更易把握[8]），因此在构型研究过程中，先研究高级次构型要素，然后在其约束下研究较低级次的构型要素，即“层次约束”。

其次，虽然开发中后期的井网密度很高，但其所控制的各级构型要素的空间分布规模仍具一定的差异性。如对于曲流河复合河道砂体侧向分布的确定性就高于点坝砂体内部泥质侧积层的分布。各级构型要素的空间分布是一定的沉积过程的结果，具有一定的分布规律[9]。开发地质学家会在充分认识这些规律的基础上建立与研究区相适应的沉积构型模式，然后将不同级次的构型模式与井资料（包括动态监测资料）拟合或匹配，建立储集层的三维构型模型，即“模式拟合”。构型地质研究必须以沉积模式为指导，具体问题具体分析。

由于各级构型要素由不同级次的界面限定，体现了沉积物的三维形态与内部岩相，故在空间上都是具有一定形态的三维地质体。如复合河道砂体呈条带或片状，单一河道呈不同弯度的条带状，点坝内部的侧积层呈新月状等。所以对于构型的研究必须突破传统的研究中依据一维井眼和二维剖面拟想出沉积体三维展布的做法，在分析过程中，使一维井眼、二维剖面和平面以及三维空间之间相互印证，建立不同层次储集层构型要素的三维分布，以反映储集层的真实情况，即“多维印证”。

2 分级套合模拟的思路

在储集层构型建模算法设计过程中，必须体现上述储集层构型研究的特点以及构型要素本身所具有的特征。最佳做法是将上述构型分析研究的思路进行数学表达和计算机实现。

本文提出的储集层构型要素建模思路中的“分级套合”源于图像分割研究领域的术语。分级套合是指对同一幅图像中不同规模的单元区域采用不同的算法进行边界识别从而分割图像[10-12]。在传统地质建模方法中，已有一些算法和研究体现了这一思路，如使用套合的变差函数刻画不同规模的两点空间相关性[13-14]，Falivene基于露头资料对重力流进行层次建模研究等[15]。

在分级套合模拟中，每个级次的模拟都依据一定的定量地质模式对每类构型要素的空间分布进行全三维模拟，并且每个大规模级次的构型要素都是下一个更精细级次构型要素模拟的信息和约束，而且每一级次的模拟均应当依据该级次构型要素的特点采用不同的模拟方法。通过这一方法建立的构型模型可反映不同级次和规模的非均质体。

依据Miall的构型分级术语，以曲流河储集层构型分析为例。首先确定5级界面（复合河道的界面），之后确定4级界面（单一河道的界面），而后再识别3级界面（河道砂体内部各类隔夹层[16]）。在分级套合模拟方法中，以这3个级次展开相互套合模拟（见图1）。

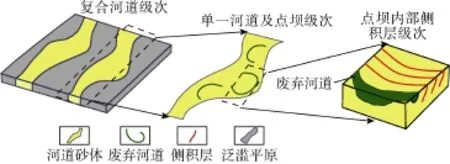
图1 分级套合模拟不同级次的曲流河储集层

3 分级套合模拟的实现

储集层三维表征主要是应用各类地质统计学的建模方法，综合多学科信息对非均质储集层空间分布进行研究。按照模拟基本单元的不同，可以将各类地质统计学方法分为基于目标和基于象元两大类[17-18]。

由于各级次储集层构型要素均具比较明确的空间形态和一定的界面信息，基于象元的方法（如序贯指示模拟Sisim）难以满足要求[19]。另有学者针对两点统计学的缺点提出了多点地质统计学算法（如Snesim）[20-21]。在多点地质统计学中，应用“数据事件”代替变差函数表达地质变量的空间结构性，一定程度上克服了传统的两点地质统计学不能再现目标几何形态的不足。但是多点地质统计学仍采取对模型中所有象元逐个计算条件概率的算法，在本质上仍然是一种基于象元的方法。虽然综合了多个条件点的空间相关信息，但在地质体的三维形态重现方面仍然存在困难[22]。

在基于目标的方法中，模拟基本单元为依据地质概念和沉积模式所定义的目标，即具有沉积相、流动单元等离散属性的一组模型网格。通过对目标几何形态，如长、宽、厚及其之间定量关系的研究，在建模过程中直接产生目标物体的整体从而建立储集层的三维模型[23]，如 Deutsch针对河流相储集层设计提出的Fluvsim方法[24]。

使用同一条件数据，通过上述 3种具有代表性的河道储集层建模算法得到的实现见图2。可以看出，在Sisim的实现中，最显著的缺点是模拟目标体不连续。Fluvsim方法则比较成功地再现了河道的几何形状。在Snesim的实现中，河道形态的完整性与 Fluvsim的结果有一定的差距。更重要的是在基于目标的方法中通过定义目标体的不同几何形状参数以及各个参数之间的地质意义，可将地质体的沉积因素考虑到模型中。本研究开发的各级储集层构型建模算法均为基于目标的方法。

图2 使用传统方法得到的河道砂体储集层模型实例

3.1 定量地质模式的约束

储集层构型的随机模拟必须受各个级次构型要素空间定量地质模式的约束，这也是构型研究中“模式拟合”要求的。所以，使用分级套合模拟方法要求对每一个级次的储集层构型分布采用定量的沉积构型模式。

国内外学者对河道砂体展布规模进行了大量的定量研究[25-27]，初步建立了高弯度曲流河沉积砂体垂向厚度与侧向规模的关系，这些定量关系是分级套合模拟方法中的主要地质依据。定量模式（见图3）分析步骤如下：①由砂体厚度（hs）经压实校正求得原始砂体厚度，这一厚度也近似等于河道满岸深度（hr）[27]。②依据满岸深度由经验公式lg Wr=1.54lg hr+0.83计算得到满岸宽度（Wr）[28]。③利用公式Wm=7.44Wr1.01计算出曲流带宽度（Wm）[29]，并按公式Wd=6.589 4Wr+0.067 7计算点坝跨度（Wd）[30]；④根据经验规模 Wl=2Wr/3计算出侧积层的水平宽度（Wl）[31]；并使用公式β= 3 3exp(- 0 .1 Wrhr)计算侧积层倾角（β）[32]。

图3 曲流河构型研究定量模式

3.2 复合河道带砂体模拟

分级套合模拟方法中，第 1级次模拟的是复合河道带砂体。单河道经过不断截弯取直和反复迁移形成了大片看似连续的河道带砂体。模拟河道带砂体应用最广的是Fluvsim方法。在此方法中，以河流相沉积的概念模型为模拟基本单元，将具有成因关系的 3种相带（河道砂体、堤岸、决口扇）投放到湖盆泥的背景沉积相中。

由于不同的河道砂体物性有差异，河道的边界会对渗流产生一定的影响[33]。构型分析在这一级次模拟中的主要目的是在连片分布的砂体中识别不同期次的河道边界，但由图2中Fluvsim的模拟实现可见，单一河道界面特征并未反映出来，这也是现有河道建模方法在构型建模中遇到的难题。

改进后的Fluvsim程序在模拟河道砂体的同时，能依据单河道的定量规模和地质模式信息将属于不同期次的河道边界作为一个离散属性记录下来，并体现在模型实现中，由图 4可见模拟实现中多个单一河道砂体的河道边界。单一期次的河道界面的刻画为后期研究砂体内部连通情况提供了依据，可以对厚砂体内部的储集层非均质进行更精细的研究。

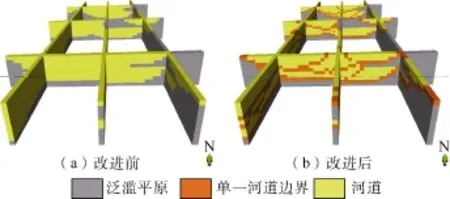
图4 改进前后Fluvsim程序模拟实现的栅状图对比

改进后的Fluvsim程序中，对当前井点目标体的投放不仅需要参考每个井点的沉积相类型，每个井点在模拟层位的砂体厚度、当前砂体的垂向叠置特征和隔夹层发育的密度等也是重要的参数。这些都是设置目标体垂向叠置关系和侧向展布特征的依据。

3.3 点坝砂体模拟

分级套合模拟的第 2个级次是模拟点坝砂体的分布。在曲流河沉积环境中，不同的曲流河会在不同弯曲状态下终止演化，并且由于后期不同的压实、保存等原因，河道砂体中的点坝呈现不同的分布样式[34]。依据沉积过程中可容纳空间和沉积物供给量比（A/S）的变化，将点坝砂体的空间组合模式分为窄条状、串珠条带状、鳞片宽带状3种模式（见图5）。

图5 随着A/S值不同而形成的点坝分布样式

目前对于点坝的空间分布样式模拟多以水动力学家、河床演变学家的研究为主，且为非条件模拟，难以对储集层构型进行三维建模[35-36]。为此，研究开发了基于示性点过程的点坝复合砂体的模拟程序Barsim，用于描述模拟物体点及其性质在空间的三维联合分布[37]。物体的性质主要是各个构型要素的长度、宽度、高度以及空间位置等。

在Barsim程序中，将井点已知的废弃河道数据、点坝砂体厚度、地层厚度等作为硬数据，从废弃河道的形态组合模式出发，圈定河道砂体内部的点坝砂体。主要步骤：①将第 1级次模拟建立的河道砂体作为背景相；②依据砂体厚度、废弃河道分布形态，随机选择一些点坝分布点，从点坝分布样式库中选出一种点坝砂体与废弃河道形状相应样式；③将这一点坝和与之相应的废弃河道作为目标体投放到模型中，检查该目标体的分布是否与某个条件信息冲突，或与以前模拟过的其他形状矛盾，如果没有矛盾，则保留该形状，否则舍弃该形状并回到上一步。④检查是否得到了各目标体的全局比例，如未满足，则回到第②步。在模拟井间区域时，应注意避免与井中已知的沉积相序列冲突。

基于中国东部某油田具体数据，利用Barsim模拟得到的结果见图6。可以看出点坝砂体的分布呈鳞片宽带状，不同的点坝砂体相互切割，由废弃河道和点坝砂体构成了极其复杂的非均质空间分布。

图6 河道砂体内单一点坝砂体的模拟

在Barsim程序中，设置了不同的点坝模式控制参数，以期最大限度地综合地质家的认识，使最终的模拟实现更具有地质逼真性（geological realistic realization）。所以，在应用Barsim程序模拟时，应该具体问题具体分析，选择不同的点坝模式控制参数，从而使结果更真实地体现储集层实际。

3.4 点坝内部侧积层模拟

最后一个级次模拟是在所圈定的点坝砂体范围内模拟发育的侧积层。侧积层垂向上一般在 0.5～1.0 m的规模，侧向上分布规模差异较大。对于侧积层的建模方法仍在探索当中。如有学者提出了二次网格加密方法[6]、层次约束下的随机抽样方法[38-39]、基于沉积过程的模拟[40]以及采用序贯指示模拟（Sisim）与人机结合再处理的方法等[41]。

由于上述方法仍属于基于象元的方法，为使所定义的网格能刻画点坝内部的侧积层，方法之一便是加密网格，这样就增加了模型的网格数，增加了计算时间，限制了随机模拟实现的个数，故而无法对构型要素的空间分布特征和分布的不确定性进行定量表征。本研究开发的程序Ihssim（Inclined heterogeneous strata simulation）则是基于空间矢量的模拟思路实现对侧积层的模拟。这种建模方法突破了传统的象元建模方法的限制。借鉴图形图像学中矢量存储的概念，将三维构型要素定义在点、线、面所限定的空间中。在模拟阶段，模型不定义网格，只是调整构型要素的参数来满足井数据。所以，不受模型网格尺寸的限制，并且由于在模拟过程中只是对构型要素的空间位置和形态定义参数进行调节，因而较传统的基于目标的模拟更易满足井的条件约束，模拟收敛速度更快，本方法细节见参考文献[42]。

由以上模拟的点坝砂体、废弃河道分布等作为模拟侧积层的约束条件，同时综合单井侧积层解释、侧积层厚度、侧积体宽度和侧积层倾角等定量信息，使用Ihssim就可以得到侧积层的模拟实现。由图7可清楚地看出点坝砂体内部侧积层的分布。

图7 点坝内部侧积体构型模拟结果

4 结论

本研究提出了一种可用于曲流河储集层构型建模的分级套合模拟思路。首先模拟复合河道带的展布特征，反映较大规模的储集层构型；之后模拟点坝砂体的空间分布；最后模拟点坝砂体内部的侧积层。这一思路源于沉积学家对地质实际的认识，符合构型研究中层次分析、模式拟合的思路。

在实现方法上，发展和开发了各级次的建模方法。对复合河道带，改进了传统的Fluvsim程序，可以刻画单一河道的边界信息；对于复合点坝的模拟，则是开发了Barsim算法，用以刻画复合点坝砂体的三维非均质特征；对于点坝砂体内部的侧积层，开发了基于空间矢量的程序 Ihssim，可以快速地实现对点坝砂体内部隔夹层的三维模拟。研究结果为精细刻画曲流河砂体非均质储集层空间分布提供了完整的解决方案。

[1] 吴胜和, 岳大力, 刘建民, 等. 地下古河道储层构型的层次建模研究[J]. 中国科学: D辑: 地球科学, 2008, 38(增刊Ⅰ): 111-121.Wu Shenghe, Yue Dali, Liu Jianmin, et al. Hierarchy modeling of subsurface palaeochannel reservoir architecture[J]. Science in China:Series D: Earth Sciences, 2008, 51(Supp.Ⅱ): 126-137.

[2] 李顺明, 宋新民, 蒋有伟, 等. 高尚堡油田砂质辫状河储集层构型与剩余油分布[J]. 石油勘探与开发, 2011, 38(4): 474-482.Li Shunming, Song Xinmin, Jiang Youwei, et al. Architecture and remaining oil distribution of the sandy braided river reservoir in the Gaoshangpu Oilfield[J]. Petroleum Exploration and Development,2011, 38(4): 474-482.

[3] Miall A D. Architectural-element analysis: A new method of facies analysis applied to fluvial deposits[J]. Earth-Science Reviews, 1985,22(4): 261-308.

[4] 赵翰卿, 付志国, 吕晓光. 储层层次分析和模式预测描述法[J].大庆石油地质与开发, 2004, 23(5): 74-77.Zhao Hanqing, Fu Zhiguo, Lü Xiaoguang. Reservoir type analysis and model prediction description method[J]. Petroleum Geology &Oilfield Development in Daqing Oilfield, 2004, 23(5): 74-77.

[5] Deutsch C V, Journel A G. GSLIB: Geostatistical software library and user’s guide[M]. New York: Oxford University Press, 1998.

[6] 吴键, 孙圆辉, 王彬, 等. 准噶尔DX18区块裂缝性火山岩储集体三维地质建模[J]. 石油勘探与开发, 2012, 39(1): 92-99.Wu Jian, Sun Yuanhui, Wang Bin, et al. 3D geological modeling of fractured volcanic reservoir bodies in Block DX18 in Junggar Basin,NW China[J]. Petroleum Exploration and Development, 2012, 39(1):92-99.

[7] 赵小庆, 鲍志东, 刘宗飞, 等. 河控三角洲水下分流河道砂体储集层构型精细分析: 以扶余油田探51区块为例[J]. 石油勘探与开发, 2013, 40(2): 181-187.Zhao Xiaoqing, Bao Zhidong, Liu Zongfei, et al. An in-depth analysis of reservoir architecture of underwater distributary channel sand bodies in a river dominated delta: A case study of T51 Block,Fuyu Oilfield[J]. Petroleum Exploration and Development, 2013,40(2): 181-187.

[8] 罗红梅, 朱毅秀, 穆星, 等. 渤海湾渤南洼陷深层湖相滩坝储集层沉积微相预测[J]. 石油勘探与开发, 2011, 38(2): 182-190.Luo Hongmei, Zhu Yixiu, Mu Xing, et al. Seismic facies prediction of lacustrine beach and bar reservoirs in the deep zone of the Bonan Subsag, Bohai Bay Basin[J]. Petroleum Exploration and Development, 2011, 38(2): 182-190.

[9] Walker R G, James N P. Facies models: Response to sea level change[M]. Ontario: Geological Association of Canada, 1992.

[10] Woodcock C, Harward V J. Nested-hierarchical scene models and image segmentation[J]. International Journal of Remote Sensing,1992, 13(16): 3167-3187.

[11] Lobo A. Image segmentation and discriminant analysis for the identification of land cover units in ecology[J]. Geoscience and Remote Sensing, 1997, 35(5): 1136-1145.

[12] Hay G J, Castilla G, Wulder M A, et al. An automated object-based approach for the multiscale image segmentation of forest scenes[J].International Journal of Applied Earth Observation and Geoinformation, 2005, 7(4): 339-359.

[13] Gringarten E, Deutsch C V. Teacher’s aide variogram interpretation and modeling[J]. Mathematical Geology, 2001, 33(4): 507-534.

[14] Kupfersberger H, Deutsch C V, Journel A G. Deriving constraints on small-scale variograms due to variograms of large-scale data[J].Mathematical Geology, 1998, 30(7): 837-851.

[15] Falivene O, Arbués P, Howell J, et al. Hierarchical geocellular facies modelling of a turbidite reservoir analogue from the Eocene of the Ainsa basin, NE Spain[J]. Marine and Petroleum Geology, 2006,23(6): 679-701.

[16] 岳大力, 吴胜和, 刘建民. 曲流河点坝地下储层构型精细解剖方法[J]. 石油学报, 2007, 28(4): 99-103.Yue Dali, Wu Shenghe, Liu Jianmin. An accurate method for anatomizing architecture of subsurface reservoir in point bar of meandering river[J]. Acta Petrolei Sinica, 2007, 28(4): 99-103.

[17] Deutsch C V. Geostatistical reservoir modeling[M]. New York:Oxford University Press, 2002.

[18] 纪淑红, 田昌炳, 石成方, 等. 高含水阶段重新认识水驱油效率[J]. 石油勘探与开发, 2012, 39(3): 338-345.Ji Shuhong, Tian Changbing, Shi Chengfang, et al. New understanding on water-oil displacement efficiency in a high water-cut stage[J].Petroleum Exploration and Development, 2012, 39(3): 338-345.

[19] Deutsch C V. A sequential indicator simulation program for categorical variables with point and block data: BlockSIS[J].Computers & Geosciences, 2006, 32(10): 1669-1681.

[20] Strebelle S. Conditional simulation of complex geological structures using multiple-point statistics[J]. Mathematical Geology, 2002, 34(1):1-21.

[21] Wang Libing. Modeling complex reservoir geometries with multiplepoint statistics[J]. Mathematical Geology, 1996, 28(7): 895-907.

[22] Zhang Tuanfeng. Incorporating geological conceptual models and interpretations into reservoir modeling using multiple-point geostatistics[J]. Earth Science Frontiers, 2008, 15(1): 26-35.

[23] Holden L, Hauge R, Skare Ø, et al. Modeling of fluvial reservoirs with object models[J]. Mathematical Geology, 1998, 30(5): 473-496.

[24] Deutsch C V, Tran T T. FLUVSIM: A program for object-based stochastic modeling of fluvial depositional systems[J]. Computers &Geosciences, 2002, 4(28): 525-535.

[25] 王家华, 卢涛, 陈凤喜, 等. 利用地质约束降低天然气概率储量的不确定性[J]. 石油勘探与开发, 2011, 38(6): 764-768.Wang Jiahua, Lu Tao, Chen Fengxi, et al. Reduction of probabilistic gas reserves uncertainty by geological constraints[J]. Petroleum Exploration and Development, 2011, 38(6): 764-768.

[26] 周银邦, 吴胜和, 计秉玉, 等. 曲流河储层构型表征研究进展[J].地球科学进展, 2011, 26(7): 695-702.Zhou Yinbang, Wu Shenghe, Ji Bingyu, et al. Research program on the characterization of fluvial reservoir architecture[J]. Advances in Earth Science, 2011, 26(7): 695-702.

[27] Bridge J S, Leeder M R. A simulation model of alluvial stratigraphy[J]. Sedimentology, 1979, 26(5): 617-644.

[28] Leeder M R. Fluviatile fining-upwards cycles and the magnitude of palaeochannels[J]. Geological Magazine, 1973, 110(3): 265-276.

[29] Leopold L B, Gordon Wolman M. River meanders[J]. GSA Bulletin,1960, 71(6): 769-793.

[30] Lorenz J C, Heinze D M, Clark J A, et al. Determination of widths of meander-belt sandstone reservoirs from vertical downhole data,Mesaverde Group, Piceance Creek basin, Colorado[J]. AAPG Bulletin, 1985, 69(5): 710-721.

[31] Allen J R L. Studies in fluviatile sedimentation: An exploratory quantitative model for the architecture of avulsion-controlled alluvial suites[J]. Sedimentary Geology, 1978, 21(2): 129-147.

[32] 周银邦, 吴胜和, 岳大力, 等. 点坝内部侧积层倾角控制因素分析及识别方法[J]. 中国石油大学学报: 自然科学版, 2009, 33(2):7-11.Zhou Yinbang, Wu Shenghe, Yue Dali, et al. Controlling factor analysis and identification method of lateral accretion shale beddings angle in point bar[J]. Journal of China University of Petroleum:Edition of Natural Science, 2009, 33(2): 7-11.

[33] Li Hongmei, Caers J. Geological modelling and history matching of multi-scale flow barriers in channelized reservoirs: Methodology and application[J]. Petroleum Geoscience, 2011, 17(1): 17-34.

[34] Constantine J A, Dunne T. Meander cutoff and the controls on the production of oxbow lakes[J]. Geology, 2008, 36 (1): 23-26.

[35] Sun Tao, Meakin P, Jøssang T, et al. A simulation model for meandering rivers[J]. Water Resources Research, 1996, 32(9):2937-2954.

[36] Pyrcz M J, Boisvert J B, Deutsch C V. ALLUVSIM: A program for event-based stochastic modeling of fluvial depositional systems[J].Computers & Geosciences, 2009, 35(8): 1671-1685.

[37] Cox D R, Isham V. Point processes[M]. London: Chapman and Hall,1980.

[38] Pranter M J, Ellison A I, Cole R D, et al. Analysis and modeling of intermediate-scale reservoir heterogeneity based on a fluvial point-bar outcrop analog, Williams Fork Formation, Piceance Basin,Colorado[J]. AAPG Bulletin, 2007, 91(7): 1025-1051.

[39] 尹艳树, 张昌民, 李少华, 等. 一种新的曲流河点坝侧积层建模方法[J]. 石油学报, 2011, 32(2): 315-319.Yin Yanshu, Zhang Changmin, Li Shaohua, et al. A new stochastic modeling method for 3-D forecasting lateral accretion beddings of point bars in meandering rivers[J]. Acta Petrolei Sinica, 2011, 32(2):315-319.

[40] 李少华, 卢文涛. 基于沉积过程的储集层随机建模方法: 以河流相储集层为例[J]. 古地理学报, 2011, 13(3): 325-333.Li Shaohua, Lu Wentao. Depositional process-based reservoir stochastic modeling: A case of fluvial reservoir modeling[J]. Journal of Paleogeography, 2011, 13(3): 325-333.

[41] 兰丽凤, 白振强, 于德水, 等. 曲流河砂体三维构型地质建模及应用[J]. 西南石油大学学报: 自然科学版, 2010, 32(4): 20-25.Lan Lifeng, Bai Zhenqiang, Yu Deshui, et al. Study on geological 3D reservoir architecture modeling of meandering reservoir and its application[J]. Journal of Southwest Petroleum University: Science& Technology Edition, 2010, 32(4): 20-25.

[42] 李宇鹏, 吴胜和, 耿丽慧, 等. 基于空间矢量的点坝砂体储层构型建模[J]. 石油学报, 2013, 34(1): 133-139.Li Yupeng, Wu Shenghe, Geng Lihui, et al. Spatial-vector-based reservoir architecture modeling of meandering point bar sand[J].Acta Petrolei Sinica, 2013, 34(1): 133-139.