三相PWM逆变器输出LC滤波器设计方法

，

（中国核动力研究设计院核反应堆系统设计技术重点实验室，四川 成都 610041）

1 引言

基于脉冲宽度调制（PWM）技术的逆变器广泛应用于各型变频及电能变换装置中。由于PWM调制技术自身的技术特性，决定了逆变器输出交流电力中含有较多的高次谐波分量，该类谐波分量的存在将直接影响交流电力品质，因而，必须在逆变器输出侧设置交流低通LC滤波器，以优化交流电力品质，在充分研究LC滤波器对逆变器传输效率及系统稳定性影响的基础上，提出了一种三相逆变器输出LC型滤波器设计方法。

2 逆变器输出交流谐波分析

PWM逆变器输出交流谐波呈如下特点：

1）谐波分量以角频率（nωC±kω1）分组分布在输出交流频谱中，其中ωC为载波角频率，ω1为信号波角频率，n，k为谐波系数；

2）每组谐波以载波角频率nωC为中心，边频为kω1分布其两侧，其幅度两侧对称衰减；

3）随着载波角频率ωC的不断增加，谐波频谱将整体向较高频带上移动［1-2］。

通过上述交流谐波分析，根据交流用电设备对电力品质的相关要求，结合LC滤波器的结构简洁、高频谐波抑制效果较好等技术特点，采用低通LC型滤波器实现逆变器输出交流电力品质优化为最佳方式。

3 交流三相LC滤波器基本结构

通常情况下，交流三相LC滤波器的基本结构主要有星形结构和三角形结构2种，其基本结构如图1所示。

图1中，L1，L2，L3代表滤波电感，且均相等，C1，C2，C3代表滤波电容，且均相等。其中，图1a为星形结构的交流三相LC滤波器，主要用于三相交流接地系统中；图1b为三角形结构的交流三相LC滤波器，主要用于三相交流不接地系统中。

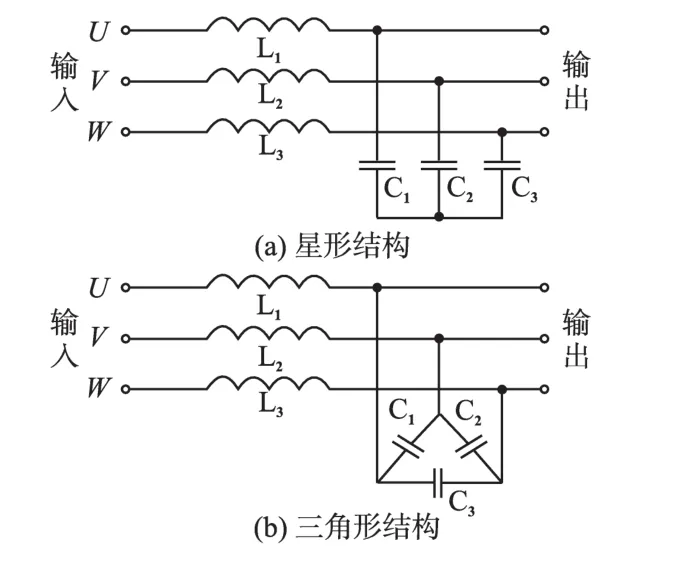
图1 交流三相LC滤波器基本结构Fig.1 The basic structure of AC there-phase LC filter

4 设计方法

4.1 设计流程

逆变器输出LC滤波参数设计流程如下：

1）根据逆变电源的载波频率fC值，确定LC滤波器的截止频率选取范围，并选定截止频率点，通常从截止频率选取范围的中间值进行选取；

2）根据电路传输理论，计算出最优传输效率下的LC滤波器的L，C值；

3）根据负载容量要求，验算此时的LC滤波器出口电力容量是否满足交流用电设备的电力容量要求；

4）根据系统稳定要求，验算此时的系统谐振频率是否符合系统稳定运行要求；

5）利用Matlab/Simulink建模与仿真平台，进行系统仿真分析验证。

4.2 设计原理

为了开展LC滤波器参数的设计，考虑到交流三相系统的对称性，需要将逆变器出口的交流三相系统转换为等效的单相系统，则得到的等效单相电路如图2所示。

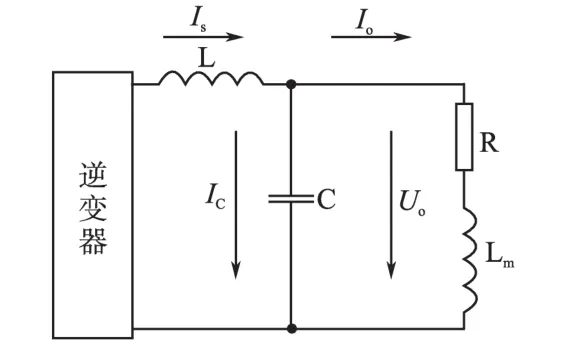
图2 逆变供电系统单相等效电路Fig.2 The single-phase equivalent circuit ofinverter power system

图2中，Is为电感电流；Io为输出相电流；IC为电容电流；Uo为输出相电压；L为单相等效滤波电感，不论采用星形结构，还是采用三角形结构，均有L=L1=L2=L3；C为单相等效滤波电容，如果采用星形结构，则有C=C1=C2=C3，如果采用三角形结构，则有C=3×C1=3×C2=3×C3；R，Lm为交流用电设备的等效阻抗参数，其中，R为等效电阻，Lm为等效电感。

4.2.1 截止频率范围确定

截止频率fC是LC滤波器的重要参量。在进行截止频率计算之前，需要做出适当的前提假设：

1）直流电源为理想电压源；

2）逆变变频电源的功率开关器件为理想开关；

3）忽略滤波电感及滤波电容的寄生参数及系统交流电力传输电缆的寄生参数。

根据时域分析法的基本原理，二阶LC滤波器的传递函数为

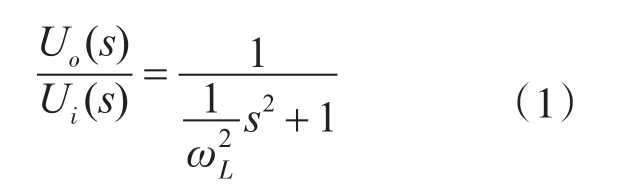
其中

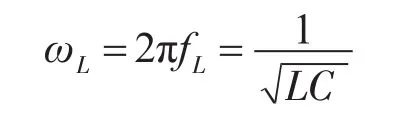
式中：fL为LC滤波器的截止频率；ωL为LC滤波器的截止角频率；Uo(s)为滤波器的输出电压；Ui(s)为滤波器的输入电压；s为拉普拉斯变换算子。

为了使得逆变器输出交流电力品质达到要求，要求LC滤波器的截止频率应远小于输出交流中最低次谐波频率，同时，又要远大于基波频率。由于逆变器的载波频率fC较高，通常在几kHz以上，远大于10倍基波频率，因而，fL选择范围为载波频率的1/10～1/5，即：

这时，即可根据式（2）得到截止频率选择范围，在计算滤波参数L，C时，可依据该范围确定具体的截止频率点，通常从其选择范围中间值进行选择［3］。

4.2.2 LC参数计算

根据LC滤波器的传递函数，其截止频率由滤波电感L和滤波电容C的乘积确定，在确定截止频率后，L和C值还需要分别确定。本文借鉴文献［3］的研究成果，得到滤波电感：

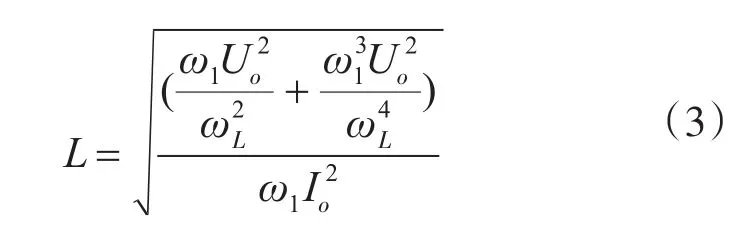
并得到滤波电容：

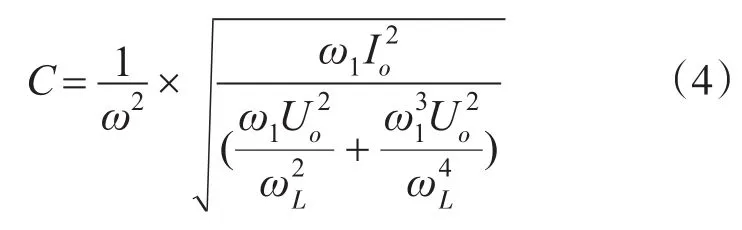
这时，可根据4.2.1节中确定的截止频率点，依据式（3）计算出该截止频率点下的滤波电感L值，再根据式（4）得到滤波电容C值，最后，利用单相电路与三相电路的电气关系，即计算出三相电路中的L和C值［3］。

4.2.3 负荷容量验算

考虑到交流用电设备的负荷要求，结合LC型滤波器为无功负载的这一特点，应对滤波器出口处的电力容量进行验算，以期验证该参数配置下的负载入口处的电力容量是否满足负载自身要求。

根据交流电路传输理论，LC滤波器出口处的电力容量的计算公式为

式中：Q为LC滤波器单相等效无功容量，则3Q为三相LC滤波器的无功容量；S为逆变器出口处的电力容量；S1为LC滤波器出口处的电力容量。

再利用交流用电设备相关计算公式，计算出其要求的电力容量，该计算公式如下：

式中：λ为交流用电设备的功率因数；P为交流用电设备的额定功率；S2为交流用电设备的电力容量，即交流用电设备要求系统提供的最小电力容量。

根据相关标准、规范等文件的具体要求，通常要求LC滤波器出口处的电力容量S1的80%应不小于交流用电设备的电力容量S2。

4.2.4 系统稳定性验算

根据图2所示，系统存在电路谐振的情况，由于电路发生谐振时，会使得系统运行不稳定，因而，应使得LC滤波器与交流用电设备之间的谐振频率尽可能远离系统运行的频率范围。

根据电路谐振基本原理，该系统主要存在滤波电容C与交流用电设备之间的并联谐振情况，因而，下面就该类谐振进行详细分析研究。

根据电路原理，可以得到滤波电容C与交流用电设备之间的并联等效导纳Y为

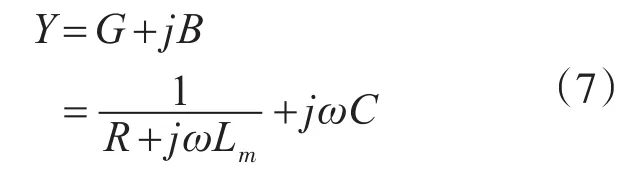
整理后，得到：

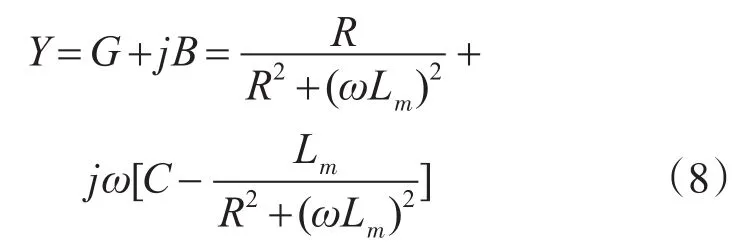
式（8）中，等效电导G为

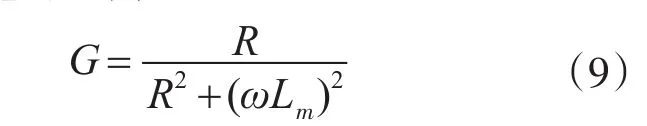
等效电纳B为

再根据并联电路谐振基本原理，其发生谐振的条件是B=0，设定谐振频率点为ωn，得到：

结合滤波电容C值及交流用电设备等效阻抗值，即可得到此时的谐振频率点，并与50 Hz比较后，即可判断出系统是否发生谐振。

考虑到会出现计算出来的系统谐振频率大于50 Hz，但又相差不大的情况，根据谐振电路的相关特性，这时，仍然存在较大发生系统谐振的可能性，由于系统发生谐振的难易程度与其谐振的品质因数有较大的关系，通常情况下，如果系统谐振品质因数越小，系统越不容易发生谐振，反之，则较易发生谐振。根据工程经验，当出现计算出来的系统谐振频率大于50 Hz但又相差不大的情况时，通常在50～250 Hz范围内，应计算此时的系统谐振品质因数，具体计算公式如下：

式中：G为等效电导；C为滤波电容；ωn为谐振角频率。

通常情况下，如果计算出的谐振品质因数满足下式的要求：

那么，可以认为即使此时的系统谐振频率存在于危险频率范围内，也几乎不可能发生谐振。

4.2.5 系统仿真验证

在前面理论计算的基础之上，利用Matlab/Simulink建模与仿真平台对该系统进行仿真验证。即利用Matlab/Simulink建模与仿真平台搭建系统模型，并将得到的相关参数值录入系统模型中，再设定Matlab/Simulink建模与仿真平台中的相关仿真参数，具体包括仿真时间、解算器选择、误差要求及步长等参数，即可启动系统仿真。完成仿真后，可利用Powergui模块对输出交流中的谐波情况进行分析，即可得到正弦性畸变率（THD）值，并可得到对应频谱图［4］。

5 工程应用

5.1 设计参数

该系统由逆变器、LC滤波器及交流用电设备组成。其主要设计参数如下：逆变电源的视在容量S=400 kV·A，输出电压U＝380 V，输出电流Io=600 A，载波频率fC=3 kHz，基波频率f1=50 Hz，LC滤波器基本结构为三角形结构，有功功率P=220kW，功率因数λ＝0.85，单相等效电阻R=1.132 Ω，单相等效电感Lm=1 324.5 μH。其设计目标为：应确保输出交流电压中的正弦性畸变率（THD）不大于5%。

5.2 LC滤波设计

5.2.1 确定LC滤波器的截止频率选取范围及截止频率点

依据4.2.1节相应公式，LC滤波器截止频率选取范围为

首次计算，选取中间值，即fL=450.0 Hz，则ωL=2 827.4 Hz。

5.2.2 计算滤波电感L和滤波电容C

依据4.2.2节相应公式，LC滤波器的单相等效滤波电感L值为：1.566×10-4H，单相等效滤波电容C值为：7.986×10-4F。

根据三相系统与单相系统的电路关系，得到三相滤波电感L三相值为：1.566×10-4H，三相滤波电容C三相值为：2.662×10-4F。

5.2.3 验算LC滤波器出口电力容量

依据4.2.3节相应公式，LC滤波器的单相等效无功容量Q为24.6 kV·A，则逆变器最终输出容量为326.2 kV·A。而交流用电负荷的需求电力容量S2为258.8 kV·A，则可以判定该参数下的LC滤波器满足负荷容量要求。

5.2.4 校验LC滤波器的系统谐振角频率

根据本实例的交流用电设备单相等效阻抗参数，结合LC滤波器单相等效滤波电容C值，并依据4.2.4节相应公式，可以得到系统谐振角频率ωn为464.2 Hz，而系统基波角频率ω1为314.2 Hz。要求系统谐振角频率在5倍基波频率以上，而系统实际谐振角频率处于基波频率与5倍基波频率之间。因而，需要对系统谐振品质因数进行校验。

依据4.2.4节相应公式，系统单相等效电纳G为0.682 S，其对应的系统谐振品质因数q为0.544，满足品质因数不大于0.707的要求。因而，该参数下的LC滤波器满足系统的稳定性要求。

5.2.5 仿真验证LC滤波器的滤波效果

利用Matlab/Simulink建模与仿真平台，进行系统仿真分析，得到该参数下的输出交流电力频谱，如图3所示。

图3 逆变器输出谐波分布图Fig.3 Harmonic distributing of inverter output

通过分析，该滤波参数下的输出电力THD值为1.89%，满足交流用电负荷的电力品质要求（交流电力中的正弦性畸变率小于5%）。

6 结论

提出了一种针对三相PWM逆变器输出交流LC型滤波参数设计方法，开展了工程应用，充分验证了该方法的可行性，对相关工程设计具有较强的指导意义。

［1］高莹，谢吉华，陈浩.SVPWM的调制及谐波分析［J］.微特电机，2006，33（7）：10-12，25.

［2］曹立威，吴胜华，张承胜，等.SPWM谐波分析的一般方法［J］.电力电子技术，2002，36（4）：62-65.

［3］俞杨威，金天均，谢文涛，等.基于PWM逆变器的LC滤波器［J］.机电工程，2007，24（5）：50-52.

［4］杜飞，杜欣.电力电子应用技术的MATLAB仿真［M］.北京：机械工业出版社，2009.