近似时间最优控制的离散域设计及其伺服应用

（福州大学电气工程与自动化学院，福建福州 350108）

1 引言

永磁交流同步伺服系统在数控加工和制造产业升级中有着举足轻重的作用，比如在服装花样缝制中，要求主轴缝纫转速达2 400 r/min，每针完成一个可编程花样长度的X Y绣框移动和定位，这类应用中几乎都要求20～30 ms的高效而快速的目标位置移动和定位，以提高加工的生产效率。通常采用的位置速度电流3闭环PI调节伺服系统却很难满足这个要求，特别在变花样长度同时需要变化主轴转速时，实验反复证明容易出现限定时间内的定位欠调或过冲。

为实现快速定位，考虑时间最优控制（TOC）［1］，即在驱动电机电流的允许极限约束下，通过正方向或反方向的最大允许幅值控制信号的施加以达到最大加速或减速的目标跟踪，这种乒乓控制由于在正负两个极端值之间切换，当现实系统存在模型差异或扰动时，系统就难免出现为克服偏差而产生颤震的现象，影响系统的应用。鉴于理想时间最优控制在这方面的缺陷，近似时间最优控制（PTOC）［1］在TOC基础上引入了一个可控的线性工作区（或称作“偏差带”），当控制目标进入该偏差带时把不易稳定的最大允许幅值控制切换到线性的PD控制，线性控制算法依据系统特性选择，并与非线性段平滑过渡衔接。由于引入小范围的线性控制，PTOC在整体快速性方面有所损失，但却获得了更好的系统鲁棒性，特别在定位完毕停车时有很好的稳定性，噪音也大大减少。

本文依据PTOC的基本思想，面向实际系统应用，寻找解决PTOC整体控制特性与系统参数之间的定量关系，进一步分析系统参数对系统性能的敏感性问题。传统PTOC控制律中并未考虑系统扰动的影响，如果系统中出现未知扰动，有可能产生目标定位的稳态误差。本文在离散时间PTOC控制基础上，采用扩展状态观测器对未知扰动进行观测估计并用于实时补偿。在增广模型中设置一个新的综合状态变量，用来描述系统的不确定性和未知扰动，随后设计观测器来估计系统的这个扰动变量，从而实现对系统的准确和鲁棒的控制。这种基于观测器的扰动补偿方案在电机伺服系统领域已得到广泛的研究［2-12］，特别是自抗扰控制（ADRC）受到了较多关注［3-6］，但ADRC的可调参数众多，在实际应用中参数的整定非常麻烦。迄今，能同时兼顾稳态准确性和瞬态性能最优化的研究成果尚少有报道。本文给出的这种基于观测器的扰动补偿近似时间最优控制方案，可以用于交流同步伺服系统上的快速且准确的位置控制。通过Matlab/Simulink仿真和基于TI公司TMS320F2812的硬件伺服系统实验，验证了控制方案的有效性和性能鲁棒性。

2 鲁棒近似时间最优控制算法

在交流永磁同步伺服系统中，传统位置控制系统是由“位置—转速—电流”3闭环组成，本文直接采用双环控制，其“位置—电流”环简化结构如图1所示。

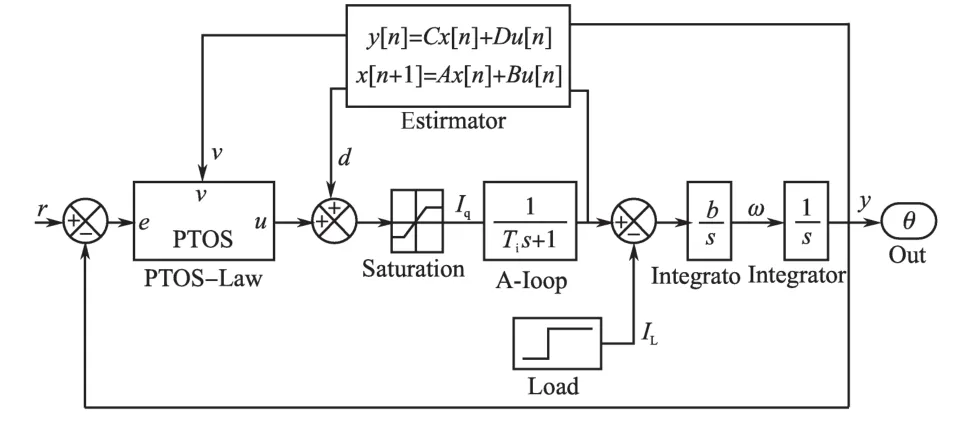
图1 控制系统结构示意图Fig.1 Schematic diagram of the control system

考虑系统中，电流环的时间常数远比位置环小得多（实际系统电流环响应时间0.5 ms左右），且其响应受外部影响很小，先忽略其对外位置环的影响，则位置控制对象的数学模型可简化为一个双积分传递函数b/s2，其中b为模型参数，主要与机电系统的惯量有关，是应用系统常见参变量之一。

在控制输入 ||u≤umax，输出量y可测条件下，可把系统模型按采样周期T进行基于零阶保持器的离散化，得到如下的离散状态空间模型：

其中

式中，输出位置y和速度v构成了状态量x；d∈R为系统中存在的慢变化未知扰动（也含模型的不确定性）， ||d＜umax；饱和限幅函数sat(u)定义为

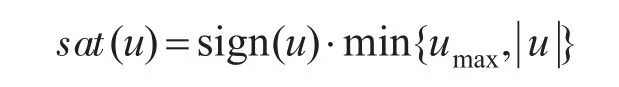
式中：sign(⋅)为符号函数。

在控制信号受限的条件下，若要使输出y快速精确地跟踪给定r，先考虑下面的时间最优控制律（TOC）：

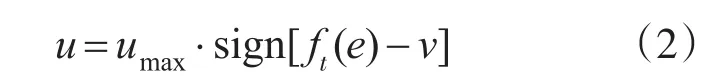
其中

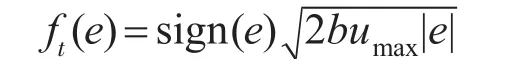
式中：e为跟踪误差，e=r-y。

如前所述TOC控制律因缺乏对系统模型差异及扰动的鲁棒性而影响了实用性，文献［1］在TOC控制律框架下引入一个线性工作区，即当误差较小时把TOC控制律切换为线性PD控制，并确保切换的平滑性。这种改进的控制方法就是近似时间最优控制（PTOC），其控制律可表述如下：

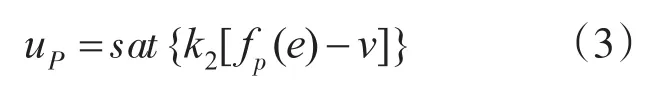
其中fp(e)函数定义为

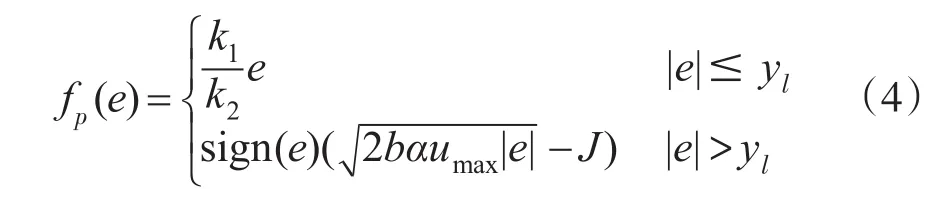
式中：yl为线性区的宽度；α为加速度折扣系数，0＜α≤ 1；J为待定的偏置量；k1，k2分别为位置和速度反馈增益。

k1和k2值可通过极点配置来确定：假如选择线性区的闭环极点阻尼系数为ζ，自然频率为ω，其对应的离散域特征方程为

其中

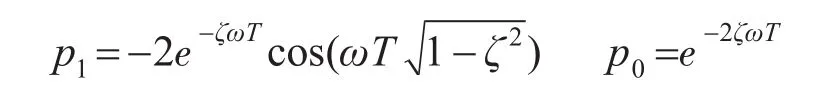
则可得到：

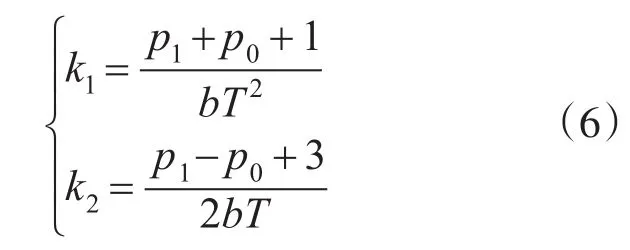
根据fp(e)函数在|e|=yl处的连续控制的平滑性要求可求得：

从式（4）～式（7）可知，在线性区小范围内可把极点自然频率ω和阻尼ζ作为可调节参数，以完成系统快速的稳定跟踪，线性工作区宽度yl选取准则应与系统的负荷惯量成比例。

式（3）的控制律中需要使用到速度信号，由于实际定位控制中，速度往往工作于较低频段（动能释放原因），考虑其传感分辨率原因引起的测量难度，本文尝试把速度和未知扰动一起归入到观测器。根据系统模型式（1）的假设条件：d(k+1)=d(k)，即扰动是常值或慢变化的，把它加入系统模型可得到一个增广系统，并按照文献［2］的方法设计一个降阶观测器来估计速度和扰动信号。若观测器极点为自然频率ω0和阻尼ζ0，则对应的离散域特征方程为

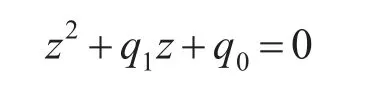
其中

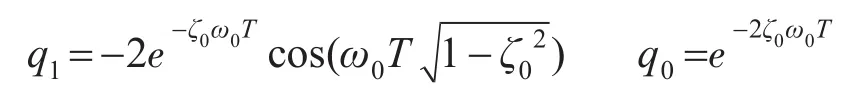
相应的观测器方程如下：

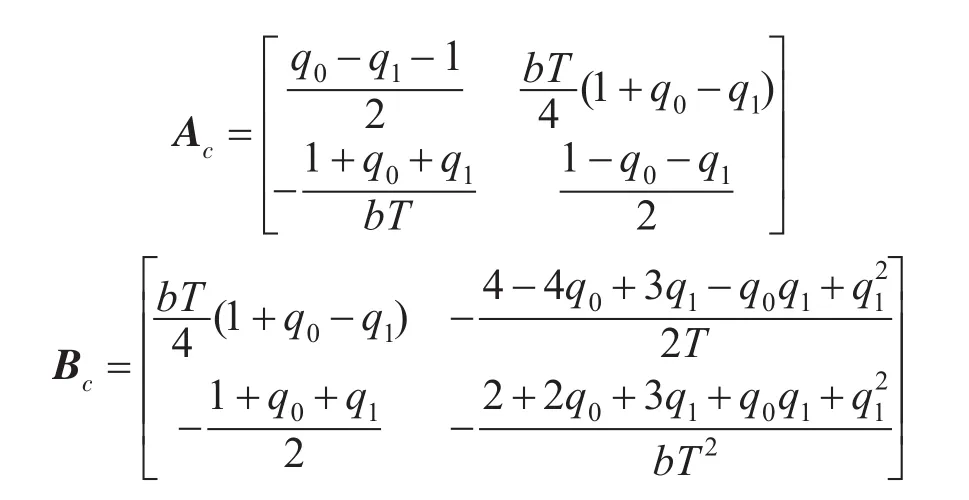
式中：xc(k)为观测器的内部状态量；分别为速度和扰动的估计值。

如果把观测器极点配置在z平面原点，即q1=q0=0，观测器的系数矩阵可以进一步简化。由于系统模型中把扰动和控制信号都合并到系统输入通道（对应同一矩阵B），则上述观测器估计出来的是一个综合（等价的）扰动信号，它既包括输入扰动，也包括可以被输入扰动等价相匹配的其他扰动和模型偏差。基于观测器式（8），在PTOC控制律中加入对扰动的补偿，最终的控制律可写成：

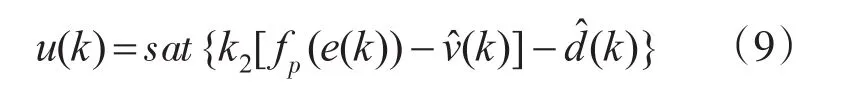
3 PMSM伺服系统的仿真分析

将上节设计的控制器应用于一个交流永磁同步伺服系统，其技术参数为：电机额定功率200 W，电机额定电流1.27 A，电机额定转速3 000 r/min，电机额定转矩0.64 N·m，电机极对数4，电机转子惯量 0.17 kg·cm2，电气时间常数2.45 ms，机械时间常数1.52 ms，反馈编码器2 500 p/r。

经测算，图1系统模型对象参数b=950（含电机及实际负载惯量）。内部电流环控制周期对应20 kHz的IGBT开关频率（周期50 μs），电流环1 ms的实际响应时间以惯性环节1/（0.001s+1）替代，以使仿真尽可能地接近实际模型，其控制输入限幅为-1.5～+1.5 A，即有：umax=1.5。

选取外部位置采样控制周期T=2 ms，控制器其他可选择参数为：α=0.7,ω=80π,ζ=0.7，ω0=20π,ζ0=0.7。其他一些关键参数由软件计算生成如下：k1=46.75,k2=0.312 7,yl=0.022 3,J=3.335 7。

首先，在Matlab/Simulink中进行仿真研究，不同目标位置的仿真结果如图2所示。图2a输入为30°阶跃转角，定位时间大约45 ms；图2b输入3圈（3×360°）阶跃转角，定位时间大约260ms；从上面可以看出系统对不同给定的目标都能快速且准确地跟踪。

图2 不同目标输入位置下的响应Fig.2 Response to different target input positions

图3的目标位置输入为360°转角阶跃，定位超调量＝0.009/3.14=0.03%，在锁定目标位置时几乎不会出现震荡现象。图4输入都为360°转角阶跃，但在目标定位过程中分别加进与运动方向相反的不同负荷，分别加进额定负载的0，40%，80%，不同负载除加减速时间有所差别外，在锁定目标位置时也几乎都不会出现震荡现象。

图3 定位过程中的响应超调Fig.3 Overshoot in the positioning process

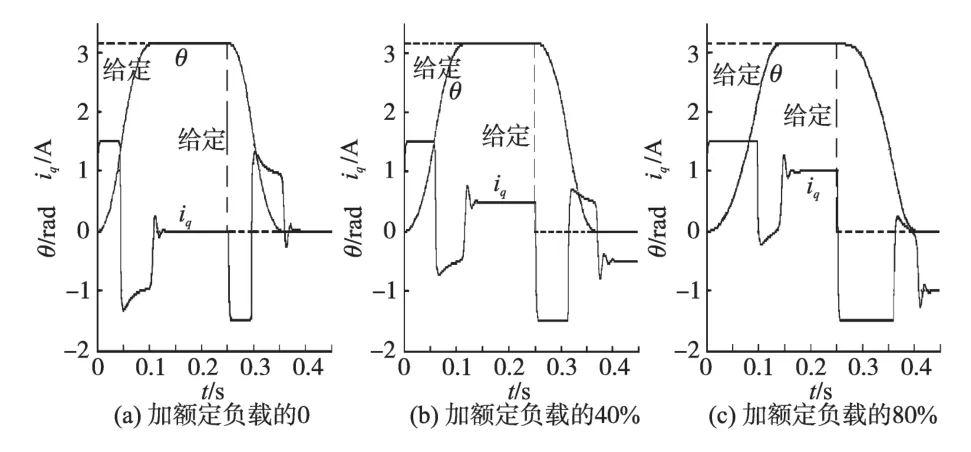
图4 不同负荷下的正反定位特性Fig.4 Position inversion under different loads

图5在定位后突然加进较大的主动负荷，图5a从0.2～1.2A（+80%），图5b从0.5～-0.77A（-100%），可以看出，最大位差＜0.05（＜1.5%），最后稳态误差为0，整个调整时间＜50 ms。显然在扰动发生跳变后输出量几乎不受影响，即扰动的影响通过观测器补偿得到了有效抑制。

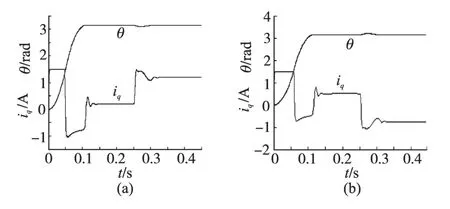
图5 抗负荷扰动的位置响应Fig.5 Anti-load disturbance position response

图6中，将含正弦变化的0.4+0.3sin(10πt)负载施加于电机上，可以看出对实现稳定的快速跟踪几乎没有影响，稳定的位置目标波动率小于0.005/3.14=0.16%，说明了扰动补偿对消除稳态误差的显著作用，扰动变化信号也能得到有效的抑制，控制系统对扰动具有较好的鲁棒性。

图6 抗周期性负荷扰动的位置响应Fig.6 Response to periodic load disturbance

从上面各种情况分析可知，不管输入指令大或小，负载的各种变化，控制算法对之均有较强适应能力，表现出相应的响应能力和抗扰动性能。

最后，分析系统对关键参数的敏感性，定义：Berr＝（实际）对象b值/（理论）PTOC计算b值。

仿真结果如图7所示。随着参数b的真实值的增大，系统响应性能趋于加快；而当b值减小时，输出响应减慢（当定位距离较远，控制信号可能多次饱和，且产生大超调）。其原因是b值的变化引起闭环阻尼发生相应的偏移。

从仿真结果看，系统在参数b值变化的较大范围（50%～100%）内仍保持较好的控制性能，具有一定的鲁棒性。

由于参数b在伺服系统中主要取决于负载惯量，如果系统需要适应更大的惯量变化时仍保持良好的瞬态性能，则应在线辨识参数b的值，一个简易的方案是在每一次定位任务结束后根据控制量u首次脱离饱和状态的时刻t1、对应的控制量u1、扰动估计量d̂1和输出位移y1来估算参数b：

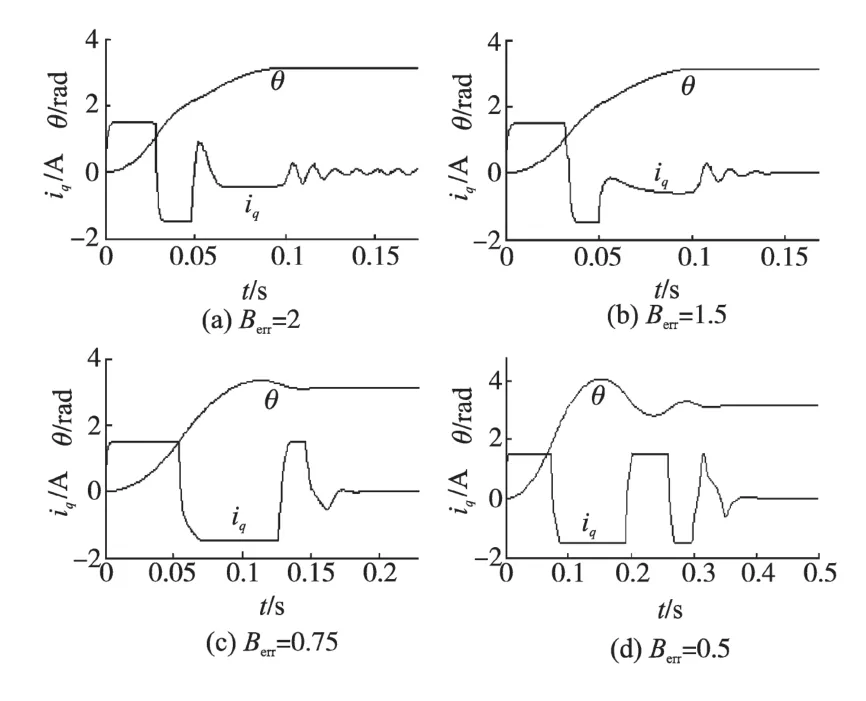
图7 系统模型参数b偏离的影响Fig.7 The influence of system model parameter

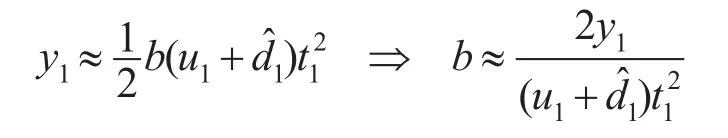
若控制开始时的控制量u不饱和，则表明其处于线性工作区，这时按线性二阶系统时域响应的超调量σ可推出当前闭环系统实际阻尼系数为

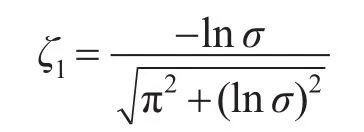
若系统无超调，则可粗略地按ζ1=1来处理。接着根据特征方程可得出受控对象的参数b1为

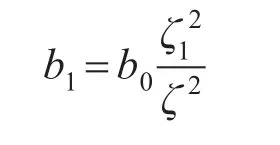
式中：b0，ζ分别为当前控制律所用的参数值。把计算得到的新值b1作为标称值用于下次控制任务。这种参数自整定方案适用于往复式位置伺服系统。

4 伺服系统的实验验证

该实验平台的主处理器为TMS320F2812，功率单元采用IPM智能模块IRAM06UP60B，以磁粉制动器作为负载，在DSP集成开发环境CCS中采集实验数据并转换到Matlab绘制波形图，由于在仿真时考虑了实际系统电流环响应和控制采样滤波等影响，实验波形图在参数适当调整后与仿真波形图基本一致。图8和图9分别是目标转角为π空载（但系统存在其他扰动）和半载（负载转矩为0.3 N·m）时的往复定位实验波形，可见系统在PTOC控制下具有快速、低超调且准确的定位性能，明显优于使用传统PID性能。

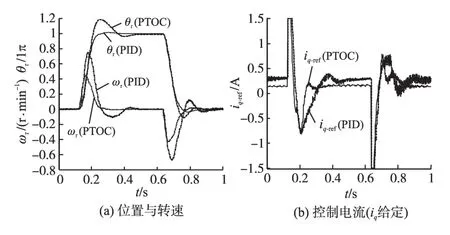
图8 目标转角为π空载时的实验结果Fig.8 Experimental results for target angleπand zero load

图9 目标转角为π负载0.3 N·m时的实验结果Fig.9 Experimental results for target angleπand load 0.3 N·m

对位置电流双环系统，由于对象具有双积分环节（参见图1），传统PID参数较难整定，通常以PD调节为主，仿真和实验表明积分很容易引起该系统闭环不稳定，但若无积分则又造成系统在不同负荷下的不同稳态误差；微分分量虽然有助于镇定该闭环系统，但过强的微分对系统扰动和噪声较为敏感。常规的做法是加入一个转速环形成3环系统，通过转速内环改善对象特性（成为单积分环节），这是现在普遍采用的结构，但也同样面临PID参数的整定和系统超调问题。图10给出了对各种输入指令（目标转角）、负载为0.2 N·m的PTOC控制性能比较（转角标幺化为1进行对比），显然，在各种情况下系统都保持原先的优越性能，具有很好的一致性。总之，伺服系统具备了近似时间最优控制（PTOC）的响应特性，其中观测器对完成时间最优控制律和广义扰动补偿起了重要作用。

图10 3种目标转角（π,2π,4π）的实验结果Fig.10 Experimental results for three target angles（π，2π，4π）

5 结论

本文给出一种位置伺服系统的鲁棒近似时间最优控制的离散域设计方案，其在时间最优控制的基础上引入一个线性工作区，当误差较小时平滑转换为PD控制律；通过扩展状态观测器来估计速度信号和各种广义扰动值，并对扰动加以补偿。在Matlab/Simulink上进行仿真研究，分析了其控制特性与系统参数之间的内在关系，并基于DSP做了永磁同步电机位置控制实验。结果表明：提出的控制方案对各种目标位置都能实现快速平稳且准确的跟踪控制，且对负载扰动和参数变化具有一定的鲁棒性。控制器采用离散时间域上的全参数化设计，方便了编程实现和实验调试，可推广应用于数控机床之类需要快速位置伺服控制的工程领域。

［1］Dhanda A Franklin G F.An Improved 2-DOF Proximate Time Optimal Servomechanism［J］.IEEE Transactions on Magnetics，2009，45（5）：2151-2164.

［2］程国扬，彭可茂，王惠.离散伺服定位系统的复合非线性控制［J］.电机与控制学报，2010，14（1）：95-101.

［3］孙凯，许镇琳，盖廓，等.基于自抗扰控制器的永磁同步电机位置伺服系统［J］.中国电机工程学报，2007，27（15）：43-46.

［4］刘志刚，李世华.基于永磁同步电机模型辨识与补偿的自抗扰控制器［J］.中国电机工程学报，2008，28（24）：118-123.

［5］滕福林，胡育文，李宏胜，等.基于自抗扰控制器的交流位置伺服系统［J］.电气传动，2011，41（11）：46-50，58.

［6］鲁文其，胡育文，梁骄雁，等.永磁同步电机伺服系统抗扰动自适应控制［J］.中国电机工程学报，2011 ，31（3）：75-81.

［7］Choi S H ，Ko J s，Kim I D，et al.Precise Position Control Using a PMSM with a Disturbance Observer Containing a System Parameter Compensator［J］.IEE Proceedings Electric Power Applications，2005，152（6）：1573-1577.

［8］王宏，于泳，徐殿国.永磁同步电动机位置伺服系统［J］.中国电机工程学报，2004，24（7）：151-155.

［9］高扬，杨明，于泳，等.基于扰动观测器的PMSM交流伺服系统低速控制［J］.中国电机工程学报，2005，25（22）：125-129.

［10］刘颖，周波，方斯琛.基于新型扰动观测器的永磁同步电机滑模控制［J］.中国电机工程学报，2010，30（9）：80-85.

［11］杨松，王毅，苏宝库.高精确度伺服转台控制系统中的扰动力矩补偿［J］.中国电机工程学报，2009，13（4）：615-619.

［12］嵇启春，孙育刚.位置伺服系统控制算法的研究［J］.电气传动，2010，40（5）：60-62.