连续潮流的研究现状及展望

李林，刘玲

(德阳电业局检修公司，四川 德阳 618000)

1 引言

随着电力市场化的改革以后，市场参与者要求增加电网的输送能力和稳定限额，将使电力系统的运行条件变得更为紧张，很容易出现电力系统电压稳定性问题[1]。在电力系统静态电压稳定性的分析中，电压稳定极限点能判断电力系统有多大的电压稳定裕度并指出采用何种适合的控制措施使电力系统运行在安全裕度之类，为调度员做出合适的预防控制措施。计算电压稳定极限点，方法有连续潮流法[2，3]、直接法[4，5]、优化算法[6]等。连续方法又称延拓法，是跟踪非线性动态系统平衡解轨迹的一种基本方法。将连续方法与电力系统静态潮流结合而产生了连续潮流法(CPF)。自20世纪90年代初提出连续潮流法以来，它在电力系统静态电压稳定性的研究方面有了长足的发展和广泛的应用，并将成为能量管理系统中一个重要模块。本文根据近年来的文献对连续潮流法加以总结和评述，并在最后对该领域的发展趋势进行了展望。

2 连续潮流的数学模型

2.1 负荷型连续潮流模型

负荷型连续潮流，主要是通过增加负荷参数，模拟系统电压随负荷参数变化的运动轨迹，得到反映系统负荷裕度的λ-V曲线，同时根据比较不同节点的λ-V曲线，识别出系统中电压的薄弱点，为预防校正控制环节提供信息。其模型为[7]:

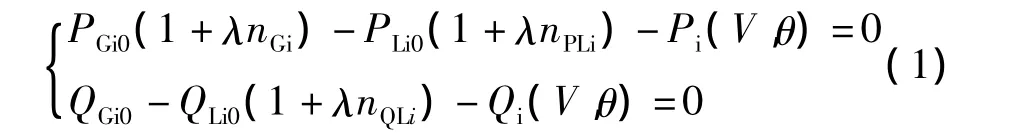
式中:λ表示发电机和负荷的增长参数，即为负荷因子;nGi、nPLi分别表示发电机和负荷有功、无功增长的方向向量;PGi0、QGi0为节点i的发电机出力;PLi0、QLi0为节点 i的负荷;Pi(V，θ)、Qi(V，θ)分别表示节点 i的有功和无功，其具体表达式如下:

式中:Vi是节点i的电压幅值;θij是节点i和节点j的电压相角差值;Gij、Bij为节点i与节点j之间的网络导纳矩阵的实部和虚部。

2.2 故障型连续潮流模型

故障型连续潮流，主要模拟系统中发电机节点或负荷节点开断故障时对系统电压的影响。文献[8]提出了一种模拟多重复杂开断故障的连续潮流模型，多重复杂故障可以看作是由多个单一故障叠加而成，而单一故障其实是多重复杂故障的一些特殊情形。

单个发电机退出的表达式为:

式中QGmax、QGmin分别表示发电机初始的无功输出上、下限。当λ=0时，节点潮流方程为发电机i没有发生故障的潮流方程;当λ=1时，节点潮流方程为发电机i退出后的潮流方程。

单个负荷退出的表达式为:

式中PLi、QLi分别为故障前负荷的有功和无功的幅值。当λ=0时，节点潮流方程为负荷i没有发生故障的潮流方程;当λ=1时，节点潮流方程就是负荷i退出后的潮流方程。

式(3)、(4)为发电机或负荷开断后的潮流方程，可以根据λ的大小判别所模拟事故是否为失稳事故，当λ＜1时，为失稳事故;当λ≥1时，事故为安全事故。

2.3 支路型连续潮流模型

支路型连续潮流，主要模拟单条支路参数变化的连续潮流模型，将参数从负荷空间转移到支路参数空间[9]。

如果线路i－m发生事故，i侧潮流模型方程为:

式中:Giinew=Gii'+λGim，Biinew=Bii'+λ(Bim－bim0)

Gii'、Bii'分别为支路i－m没有发生事故时系统导纳矩阵的自导和自纳;bim0为线路i－m初始运行时的电纳。支路型连续潮流判断失稳标准和故障型连续潮流类似，当λ＜1时，为失稳事故;当λ≥1时，为安全事故。

3 连续潮流的研究内容

3.1 连续潮流基本算法的研究

连续潮流的基本原理是通过引入连续参数采用预估校正技术，在每一点进行反复迭代，计算出准确的潮流解。众多学者在预估、校正、参数化和步长控制环节上对基本算法的研究，其目的就是加快计算速度，使其能够成为在线应用。

(1)预估环节。预估的作用是找到一个近似潮流解，为下一步校正时解扩展潮流方程提供一个初始值，所以预估时的近似值要尽可能的接近潮流的实际值，校正过程需要的迭代步数才会越少。在一些文献中已经提到了几种不同的预测方法，这些方法可以分为两类:线性预估和非线性预估。最早提出的切线法和割线法预估就属于线性预估方法，后来提出了利用非线性外推技术的方法，最常用的是插值法。文献[10]利用拉格朗日非线性插值方法进行预估，使预估值更接近潮流的真实值，减少了校正时的迭代步数。

(2)校正环节。在通过预估步骤后得到一个估计值之后，需要通过误差的校正来获得实际值。原则上来说，非线性代数方程组求解的有效数值分析方法均能用来校正这个误差。而且如果预估环节能给出实际值邻域内的一个比较好的估计值，只需很少的迭代步数便能达到所要求的精度。通常采用的校正方法有牛顿法和拟牛顿法等。文献[11]在校正环节采用快速解耦法来计算最大功率点加快了计算速度。

(3)参数化环节。参数化就是构造一个方程，使参数化方程和潮流方程构成一个具有n+1个待求变量的n+1维的扩展潮流方程组，从而避免了增广后雅可比矩阵在最大功率处奇异、病态。目前参数化有:自然参数化、局部参数化、弧长参数化、几何参数化和传输线功率损耗参数化等。

(4)步长控制环节。步长控制是连续潮流法中的一个关键的环节，步长过小将造成预估校正计算点数太多，步长过大将使得校正过程迭代次数过多、收敛缓慢甚至发散。目前步长控制策略都是根据扩展潮流方程绘制出的曲线进行控制，随着曲线的曲率大小进行变化，在曲线平坦部分采用大步长，在曲率大的部分采用小步长。文献[12]提出一种改进的步长控制连续性潮流计算方法。该方法在传统连续性方法的基础上，根据预测环节中得到的信息，自动调节步长，从而确保系统内的各离散事件能够按照实际的顺序进行调整。

3.2 静态ATC计算研究

基于连续潮流进行可用输电能力(available transfer capability，ATC)计算，采用的是负荷型连续潮流模型计算静态电压稳定的极限功率点。由于常规潮流方法的潮流雅克比矩阵在极限功率点发生奇异，引起潮流发散，而连续潮流法可以从当前运行点出发，通过逐步增加负荷参数来增加负荷的输送功率，进行反复迭代求解，可以得到极限功率点相应的发电功率，因而可以用来直接计算静态电压稳定安全约束条件下的ATC。当系统中发电机的功率或负荷发生缓慢变化时，若用P0和Q0表示系统当前状态下节点的有功与无功向量，可以将系统方程参数化为[13]:

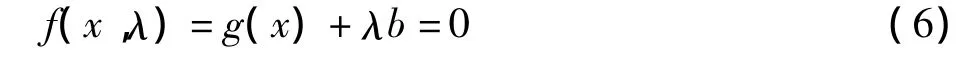
其中 b=[P －P0，Q －Q0]T，表示系统节点功率注入变化的方向向量，λ表示发电机和负荷的增长参数。b决定了当母线注入变化为λ时，系统母线负荷和发电机功率相应的变化模式。于是，可将ATC的求解问题转化为求解从一个基态情况(P0，Q0)出发，沿方向b变化的输送功率，追踪PV曲线直至电压静态稳定极限时λ的最大值。

此类方法能够很好的追踪系统实际运行的轨迹，因而计算所获得的输电极限更具有实际价值;另外这种方法可以根据需要考虑各种安全约束条件，比如:电压稳定安全约束条件、无功功率安全约束条件以及其他动态稳定安全约束条件等。并且算法有着良好的鲁棒性和灵活性，可以与现有的稳定算法(如优化算法)相结合，满足用户的不同需求。

3.3 连续潮流获取稳定极限边界的研究

利用连续潮流法在注人空间的各个方向上追踪稳定域的边界点是连续方法的另一个主要应用。通常连续潮流计算得到的静态电压稳定临界点亦即系统潮流方程的奇异点的集合，被认为是静态电压稳定域的边界。如果可以将稳定域边界完整的描述出来，就可以很快判断当前运行点在域中的相对位置和当前系统的稳定裕度。连续潮流中引入单个参数可得到在不同参数下的潮流解，这些潮流解在二维平面内构成了一条曲线，即PV曲线，但对于稳定域来说，只得到稳定域边界上的一个点，这个点就是潮流雅克比矩阵的奇异点。若引入两个自由参数的变化则可以得到三维空间中的曲面，获得的稳定域边界是一条曲线，这条曲线就是在不同负荷参数下潮流雅克比矩阵的奇异点的集合。文献[14]利用连续潮流和优化算法的混合方法，将边界计算问题转化为一个以域外某点到边界面距离最小为目标函数的优化问题，计算出高维空间中与当前运行点相对应的最近边界点，同时可计及系统中设备的限值，实现了在二维空间可行域边界的可视化。文献[15]基于特征值灵敏度和特征向量灵敏度的计算，通过对潮流方程雅可比矩阵的行列式在临界点附近进行泰勒级数展开并保留二次项，得到了计及非线性项的边界近似解析表达式。

4 对连续潮流法的进一步展望

连续潮流无论是基本算法研究和应用研究都取得了不同程度的发展，其鲁棒性和控制指导作用愈来愈强。但是，面对日益庞大和复杂的电力系统，连续潮流法在以下方面仍然值得我们探讨。

(1)对于基本算法的改进。在连续潮流中一定要保证基本算法的速度和精度。因此，不论是连续潮流基本算法的系统理论、关于计算的软件都应该进行不断的改进。力求以更快的计算速度，更好的鲁棒性获得更精确的计算结果。

(2)连续潮流中元件模型的完善。在连续潮流中应建立起符合系统实际方向的元件模型，挖掘系统实际的运行特点和影响因素。比如，在潮流负荷中计及感应电动机动态特性、在潮流模型中考虑 SVC等FACTS设备的模拟，研究它们的动态特性对系统静态稳定性的影响等。

(3)连续潮流法与动态潮流相结合。连续潮流法与微分代数方程组(DAE)平衡点的非线性系统数学模型方程相结合，可以得到电力系统动态稳定域上的各种类型分岔点。

(4)开展连续潮流的在线分析研究，满足实时可用输电能力计算要求。可用输电能力作为电力系统可靠性和安全性的重要指标，己成为能量管理系统分析功能的重要组成模块，开展实时环境下的可用输电能力研究对互联电力系统安全的预防与控制具有重要意义。

5 结论

本文从连续潮流的三种数学模型出发，总结和评述了连续潮流基本算法、静态ATA计算和获取稳定极限边界的研究方法，并对连续潮流进行了进一步的展望。连续潮流法为解决电力系统静态电压稳定问题提供了实用的理论支持，成功应用于计算机技术的在线分析，并将成为能量管理系统中一个重要模块。

[1]李林，康积涛，张学群，等.感应电动机参数对小干扰电压稳定影响[J].四川电力技术，2010，33(3)：68 －70.

[2]Chiang H D，Flueck A J，Shah K S，et al.CPFLOW：A Practical Tool for Tracing Power System Steady-state Stationary Behavior Due to Load and Generation Variations[J].IEEE Transactions on Power Systems，1995，10(2)：623 －634.

[3]Dilson A.Alves，Luiz C.P.，da Silva et al.Continuation fast decoupled power flow with secant predictor[J].IEEE Transactions on Power Systems，2003，18(3)：1078 －1085.

[4]刘永强，严正，倪以信.基于辅助变量的潮流方程二次转折分岔点的直接算法[J].中国电机工程学报，2003，23(5)：9 －13.

[5]ROSEHART W.D，CANIZARES C.A，QUINTANA V.H.Multi-objective optimal power flows to evaluate voltage security cost in power networks[J].IEEE Trans on Power Systems，2003，18(2)：578 －587.

[6]Irisarri G D，Wang X，Tong J，et al.Maximum loadability of power systems using interior point non-linear optimization method[J].IEEE Trans on Power Systems，1997，12(1)：162 －169.

[7]周双喜，朱凌志，郭锡玖，等.电力系统电压稳定性及其控制[M].中国电力出版社，2004.

[8]赵晋泉，江晓东，张伯明.一种用于静态稳定分析的故障参数化连续潮流模型[J].电力系统自动化，2004，28(14)：45 －49.

[9]Flueck AJ，Dondeti J R.A New Continuation Power Flow Tool for Investigating the Nonlinear Effects of Transmission Branch Parameter Variations[J].IEEE Trans on Power Systems，2000，15(1)：223 －227.

[10]Mori H，Yamada S.Continuation power flow with the nonlinear predictor of the Lagrange's polynomial interpolation formula[J].Transmission and Distribution Conference and Exhibition 2002：Asia Pacific，IEEE/PES，2：1133 –1138.

[11]Alves D A，da Silva L C P，Castro et al.Continuation fast decoupled power flow with secant predictor[J].IEEE Trans.on Power Systems，2003，18(3)：1078 －1085.

[12]王成山，魏炜.一种改进的步长控制连续性潮流计算方法[J].电工技术学报，2004，19(2)：58 －63.

[13]刘皓明，倪以信，吴军基，等.计算电网可用输电能力的方法述评[J].继电器，2003，31(10)：45 －50.

[14]余贻鑫，李鹏，贾宏杰.基于混合法的潮流可行域边界计算[J].电力系统自动化，2004，28(13)：18 －25.

[15]韩琪，余贻鑫，贾宏杰.静态电压稳定域边界的非线性近似解析表达[J].电力系统自动化，2005，29(11)：10 －14.