连续消耗应急物资调运问题研究*

童晓进，符卓，刘勇，2，黄珊，文成龙

(1.中南大学交通运输工程学院，湖南长沙 410075;2.广西百色军分区后勤部，广西百色 533000)

在大规模突发事件的救援工作中，应急物资调运是救援工作的重要保障。连续消耗应急物资调运问题的重要特征是引入了应急点对应急物资的消耗速率概念，且要求应急物资一旦开始参与救援，就必须保证物资能持续消耗直至物资需求得到满足为止。该问题在大规模突发事件的救援工作中普遍存在，诸如连续性应急生产原料供给、电力供应等。目前，刘春林等［1－3］研究了应急救援出救点选址等问题，针对多出救点组合问题，提出了关于应急物资调度完成时间最短和出救点数目最少的优化模型及算法;戴更新等［4］针对多资源多出救点问题，研究了多资源最短应急时间问题的数学模型;张彦春等［5］结合铁路运输特点，对一次性消耗应急物资调配模型进行了研究;高淑萍等［6］从应急系统费用和可靠性的角度考虑，将出救点的数目最少作为优化目标，给出了连续消耗应急物资调运两层优化数学模型及求解方法。

在连续消耗应急物资调运问题上，已有文献主要侧重于物资参与救援开始时间(即出救点物资调运开始后，物资到达应急点并参与救援的时间)问题的研究，对出救点数目优化问题研究相对较少且计算较为繁琐。本文在上述文献的研究基础之上，以多出救点、单应急点的连续消耗应急物资调运问题为研究对象，在满足物资参与救援开始时间最早的基础上，给出了出救点数目优化过程的3个判断条件，并利用分层序列思想设计了简单的求解算法。

1 问题描述及分析

设B地区发生大规模突发事件，对某连续消耗应急物资的需求量为b，在该物资参与救援开始后，其平均消耗速率为v。现有m个应急物资供应点A1，A2，…，Am可以参与救援，该应急物资储备量分别为 a1，a2，…，am，且ai≥b。在救援工作中，Ai实际调往B的应急物资量为xi，即有=b，且从Ai到B的运输时间为ti。要求在满足连续消耗型物资调运的要求下，给出一个调运方案φ(确定最终的出救点及其物资调运量)，使物资参与救援的开始时间最早，出救点数目最少。

这是1个多目标规划问题，若非劣解只有1个，则该非劣解即最优解;若非劣解不止1个，则必须按照预定的规则选出1个认为是比较好的解，即“选好解”［7］。在应急物资调运问题中，应遵循时间效率重于经济效益的设计原则［8］。因此，本文遵循这样一个“预定的规则”:以物资参与救援开始时间最早为第一目标，以出救点数目最少为第二目标，由此得到最终的调运方案。

2 建立模型

设调运方案φ表示为:

其中:i1，i2，…，im为1，2，…，m 的1 个子排列，且满足=b，0 ≤ xik≤ aik，在本文中，不妨设 i0=0，ti0=0，xi0=0，ai0=0。为了便于分析，给出如下定义。

定义1 对于序列 xi1，xi2，…，xim，若存在p(1≤p≤m)使得 ＜b≤ 成立，则称p为该序列相对于b的临界下标。

此时，调运方案φ可进一步表示为

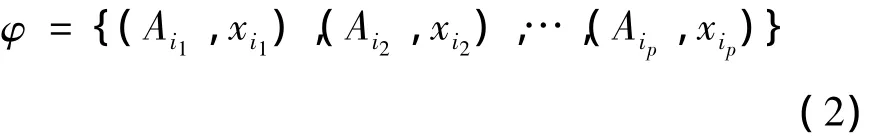
按照“预定的规则”，首先考虑满足物资参与救援开始时间最早的要求。那么凭经验很容易就能得到使应急点获得物资救援最早的办法(以下简称经验法)是:由离应急点运输时间最短的物资供应点参与救援，在供给不足以满足需求的情况下，离应急点运输时间次短的物资供应点参与救援，依此类推，直到应急点需求得到满足为止。然而，因该方法并未考虑该问题的应急物资具有连续消耗的特征，在物资参与救援开始后，应急点的物资消耗可能因供给不足而出现中断的情况，故该方法不一定能满足物资连续消耗的要求。此时，引入方案φ关于物资参与救援开始时间s连续可行的定义:设s表示物资参与救援的开始时间，f表示应急点对该物资消耗的结束时间，根据连续消耗应急物资的特点，有

定义2 若在方案φ中，对于 ∀t∈［s，f］，下式始终成立，则称方案φ关于物资参与救援的开始时间s连续可行［6］，即在物资参与救援开始之后，能保证物资供给量不小于消耗量。

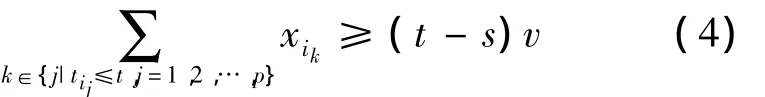
定义3 若方案φ关于物资参与救援开始时间s连续可行，则称方案φ为可行方案，称由可行方案组成的集合为χ。

因此，关于物资参与救援开始时间s最早的目标函数可表示为

此外，由定义2可演算得到如下定理。

定理1 若方案φ关于物资参与救援的开始时间s连续可行，则s应满足:

在式(6)中， 表示前k－1个出救点的救援物资可维持消耗时间。若hik≤0，表示在该方案中，出救点Aik始终能与前k－1个出救点保持物资的连续消耗;若hik＞0，则表示为使Aik的物资能与前k－1个出救点保持连续消耗，需要在调运开始后过hik个单位时间才能参与救援，即至少在调运开始后过max{hik}个单位时间参与救援才能保证方案φ关于s连续可行。因此，方案中物资参与救援的最早开始时间取s=max{hik}。

其次考虑优化出救点数目问题，为分析该问题，引入0－1变量zik来表示Aik是否参与救援，并令

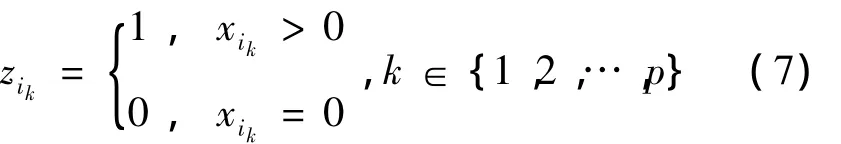
即出救点数目可表示为

因此，该连续消耗应急物资调运问题的数学模型可以表示为

目标函数(9)式表示该连续消耗应急物资参与救援开始时间最早;目标函数(10)式表示出救点数目最少;约束条件(11)式表示物资参与救援开始后，对于任意时刻t，方案始终关于参与救援开始时间s连续可行;约束条件式(12)表示各出救点参与救援的物资量不超过其物资储存量。

3 模型求解

求解多目标规划问题的方法主要有:化多目标为单目标、引进次序法、直接求非劣解法等。由于应急物资调运具有时间效率高于经济效益的特点，在此利用分层序列思想设计求解算法。首先对应急物资参与救援开始时间最早(函数(9))进行求解，得到应急物资参与救援开始时间最早的可行方案;在此基础上对出救点数目(函数(10))进行优化，从而求得该问题的最终调运方案。

3.1 参与救援开始时间最早的可行方案

利用上述经验法得到的调运方案，使物资参与救援开始时间s最早，但方案不能保证关于s连续可行。因此，在经验法的基础之上添加关于s连续可行的约束条件，即约束条件(11)和(12)，则容易得到满足物资参与救援开始时间最早的可行方案，这在文献［9］中已经得到证明。

不妨设t1≤t2≤…≤tm，则物资参与救援开始时间最早的方案是:按ti(1≤i≤m)从小到大的顺序依次安排Ai参与救援，直到p为相对b的临界下标，即

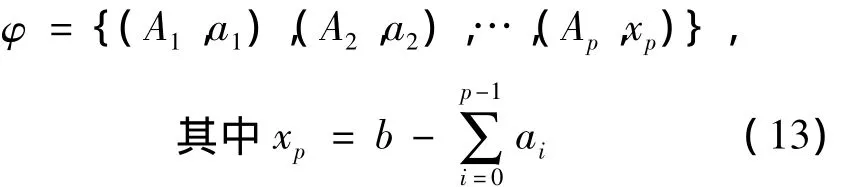
为保证方案关于s连续可行，在满足约束条件(11)和(12)的要求下，得到物资参与救援的最早开始时间为

此时，方案φ满足物资参与救援开始时间最早，且为可行方案。

3.2 优化出救点数目

上述方案φ是本问题的初始方案，实现了物资参与救援的开始时间最早且方案关于S连续可行，但有时会存在Ap物资有剩余的情况，因此，出救点数目存在优化的可能性［10］。此时，在满足约束条件(11)和(12)的要求下，对初始方案φ的出救点数目进行优化。

(1)出救点Ap剩余物资量大于Aq参与救援的物资量。即Ap所剩余的物资量为ap－xp，Aq参与救援物资量为aq，则aq须满足

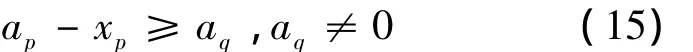
(2)物资参与救援的最早开始时间s不变。即Aq下标q须满足

现利用反证法对式(16)进行证明:假设存在出救点Aq(q＜y)被取代，方案关于物资参与救援的最早开始时间S能保持不变。已知在Aq被取代后，物资参与救援的最早开始时间s'=max{hk}，k∈ {1，2，…，(q － 1)，(q+1)，…，y，…p}，显然有Δs=s'－ s=aq/v，Δs＞ 0，故假设不成立。因此，取y≤q≤p－1。

(3)方案始终关于物资参与救援的开始时间连续可行，则tq须满足

3.3 计算步骤

第1步，按照式(13)和(14)获得参与救援开始时间最早的一个初始可行方案φ，有φ={(A1，a1)，(A2，a2)，…，(Ap，xp)}。其中:xp=b － ，且S=k∈{m1，2a，x…，p}{hk}，hk=tk－ 。

第2步，将同时满足判断条件(1)，(2)和(3)的出救点组成集合R1(R1={Aj}，j为符合上述3个判断条件的出救点下标)。显然有R1⊆R。若R1=φ，则跳到第5步，否则进入下一步。

第 3 步，Aq∈R1，令q=max{j}，设aq=0，计算 S'=max{hk}，k∈ {1，2，…，(q － 1)，(q+1)，…，p}，并进入下一步。

第4步，验算s'=s是否成立。若成立则置aq=0并返回第1步;否则将Aq从R1中删除，重复第3步直到R1=φ时，进入第5步。

第5步，计算结束，此时方案φ即为本问题的最终调运方案。

4 算例分析

某地区B发生大规模突发事件后，亟需某类连续消耗应急物资，需求量为16 t，在物资参与救援开始后，其平均消耗速率为1 t/h，能参与救援的物资供应点有8个，其相应的数据信息如表1所示。

表1 仿真结果Table 1 Simulation data

通过对上述问题的分析，利用本文给出的模型及算法进行求解。首先计算得到满足参与救援开始时间最早的初始可行方案如下:

按此调运方案，在物资调运开始后过2 h，该救援物资即可参与救援，从而使物资参与救援开始时间最早，并满足关于救援开始时间s连续可行的要求。

然后，利用上述的计算步骤对初始可行方案进行优化，其计算过程如表2所示。

表2 计算过程Table 2 Computation process

因此，在该算例中，最终的调运方案为φ ={(A1，5)，(A2，0)，(A3，0)，(A4，11)}，且 s=2

即物资参与救援的最早开始时间是物资调运开始后过2 h进行，只需2个出救点A1和A4。

5 结论

(1)以物资参与救援开始时间最早、出救点数目最少为目标，对连续消耗应急物资调运问题进行了研究，建立了相应的多目标优化决策模型。在满足物资参与救援开始时间最早的基础上，给出了出救点数目优化过程的3个判断条件，并利用分层序列的思想设计了简单的求解算法，最后通过算例验证了模型及算法的有效性。

(2)本文给出的调运方案计算方法可为决策者提供决策依据，也为物资供求关系不确定、多应急点等更复杂情况下的连续消耗应急物资调运问题研究打下了基础。

［1］刘春林，何建敏，盛昭瀚.应急系统调度问题的模糊规划方法［J］.系统工程学报，1999，14(4):351－355，365.LIU Chunlin，HE Jianmin，SHENG Zhaohan.Fuzzy programming for scheduling problem in emergency systems［J］.Journal of Systems Engineering，1999，14(4):351－355，365.

［2］刘春林，何建敏，施建军.一类应急物资调度的优化模型研究［J］.中国管理科学，2001，9(3):29－36.LIU Chunlin，HE Jianmin，SHIJianjun.The study on optimal model for a kind of emergency material dispatch problem［J］.Chinese Journal of Management Science，2001，9(3):29 －36.

［3］何建敏，刘春林，尤海燕.应急系统多出救点的选择问题［J］.系统工程理论与实践，2001，21(11):89－93.HE Jianmin，LIU Chunlin，YOU Haiyan.Selection of multi－depot in emergency system［J］.Systems Engineering Theory＆ Practice，2001，21(11):89－93.

［4］戴更新，达庆利.多资源组合应急调度问题的研究［J］.系统工程理论与实践，2000，20(9):52－55.DAI Gengxin，DA Qingli.The study of combinational scheduling problem in emergency systems［J］.Systems Engineering Theory＆ Practice，2000，20(9):52－55.

［5］张彦春，范艳萍，杨小礼.铁路突发事件应急物资优化调配［J］.铁道科学与工程学报，2011，8(6):103－106.ZHANG Yanchun，FAN Yanping，YANG Xiaoli.Optimization on railway emergency material dispatching［J］.Journal of Railway Science and Engineering，2011，8(6):103－106.

［6］高淑萍，刘三阳.应急物资调度问题的最优决策［J］.系统工程与电子技术，2003，25(10):1222－1224.GAO Shuping，LIU Sanyang.Optimal decision for scheduling problem in emergency systems［J］.Systems Engineering and Eectronics，2003，25(10):1222 －1224.

［7］汤代焱，等.运筹学［M］.长沙:中南大学出版社，2007.TANG Daiyan，et al.Operational research［M］.Changsha:Central South University Press，2007.

［8］蔡鉴明，李夏苗，杨光华.基于时变性和可靠性的地震灾害应急物流运输路径选择［J］.铁道科学与工程学报，2011，8(5):101－106.CAI Jianming，LI Xiamiao，YANG Guanghua.The routing problem for emergency logistics considering the reliability and time － varying in the earthquake disasters［J］.Journal of Railway Science and Engineering，2011，8(5):101－106.

［9］刘春林，盛昭瀚，何建敏.基于连续消耗应急系统的多出救点选择问题［J］.管理工程学报，1999，3(13):13－15.LIU Chunlin，SHENGZhaohan，HEJianmin.Selection of multi－depot based on emergency system for the continuous consumption［J］.Journal of Industrial Engineering Management，1999，13(3):13 －15.

［10］吴诗辉，杨建军.一次性消耗的应急系统资源调度问题研究［J］.物流科技，2009，32(7):47－49.WU Shihui，YANG Jianjun.The study of material dispatch problem for the one－time used－up emergency response system［J］.Logistics Sci－ tech，2009，32(7):47－49.