开槽钝锥体及等离子体鞘套的RCS特性研究

梁世昌，于哲峰，张志成，石安华，马 平，黄 洁

(中国空气动力研究与发展中心，四川绵阳 621000)

0 引言

随着再入突防技术的发展，在超高速飞行体表面开切凹槽并填充各种介质材料已经成为调整目标电磁散射特性的重要途径之一［1］。比如在多目标飞行时，通过开槽提高假目标的电磁散射特性，从而达到隐蔽真实目标的目的。因此，分析钝锥体在超高速飞行中等离子体鞘套和开槽对其电磁散射特性的影响具有重要的实际意义和应用前景。

在分析这类金属目标上开槽并填充介质后的电磁散射问题时，高频近似方法失效，除了极少数简单典型体的电磁散射能用解析法求解外，其它问题只能借助于数值方法。常用的数值分析方法有时域有限差分法(FDTD)、矩量法、有限元法等。但是对于电大尺寸的飞行目标又具有电小尺寸的缝和槽的问题，相比较而言，还是时域有限差分法具有更大的优势和更好的实用性。

采用FDTD方法研究等离子体鞘套包覆目标的电磁散射特性，发展基于FDTD方法的超高速飞行器及其等离子体鞘套的RCS特性并行计算分析软件，分析一种开槽并填充透波性能良好介质材料的超高速钝锥体的电磁散射问题，同时考虑了钝锥体在超高速飞行时绕流场等离子体鞘套的影响，得到一些有意义的结论。

1 计算方法

等离子体可以看作是一种色散介质，在利用FDTD方法计算目标及其绕流场等离子体鞘套的雷达散射截面时需要对等离子体进行特殊处理，处理方法有多种，常用的有直接积分方法［2］、分段线性递归卷积法［3］、Z 变换法［4］、方向交替隐式法［5-6］等，或几种方法的混合求解［7-8］。直接积分方法需要较少的存储单元，计算效率较高，计算精度也较精确。本文采用直接积分方法研究等离子体包覆目标的RCS。

考虑目标的金属表面覆盖着一层非磁化冷等离子体，等离子体中的离子因其大的质量而忽略其运动。此时Maxwell方程可以写为：

其中，E和H分别为电场强度和磁场强度，J为电流密度，μ0和ε0分别为真空中的磁导系数和介电常数，ν和ωp分别为电子碰撞频率和等离子体频率。

采用J.L.Young等人提出的直接积分方法［2］对方程组(1)的第三式进行离散，有：

得到x分量的显式差分方程表示为：

电磁场的其它分量可同样推出。

在采用FDTD方法计算电磁场时，目标的电尺寸越大，需要的网格数目越多，内存随之增大，计算所需的时间步也会随之增加，并行算法是解决这一问题的有效途径之一。利用 MPI并行技术研制了基于FDTD方法的超高速飞行器及其等离子体鞘套的RCS特性计算分析软件。

在进行FDTD并行算法设计时需要对计算任务进行空间和时间上的合理分割，以适应不同计算节点加载不同计算任务。从FDTD方法模拟电磁波在时间上由前至后的过程特点及人们理解客观现象发生顺序的思维定势角度看，首要是计算任务的空间分割——即空间并行，其次才是不同计算任务之间时间的完全并行化。算法设计还包含其它外围问题处理的设计和流程，这些FDTD外围相关问题包括：计算模型的分割、吸收边界的分割、连接边界的分割、近远场变换积分面的分割及各节点计算任务平衡问题等。

采用发展的RCS并行计算软件计算了半径为0.2m的纯等离子球的RCS，入射波频率1GHz，等离子体频率3GHz，碰撞频率1GHz。图1和2是计算得到的其E平面和H平面的双站RCS与Mie级数解的对比，可以看出计算结果和Mie级数解一致，这说明本文发展的RCS计算软件是可靠的。

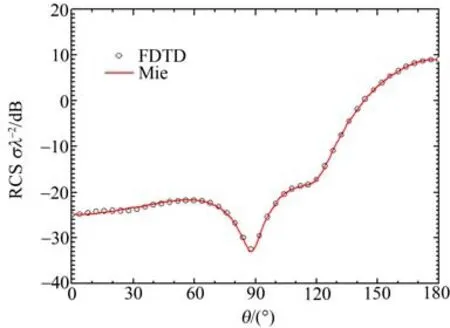
图1 E平面非磁化等离子体球的双站RCSFig.1 Bistatic RCSof nonmagnetic plasma sphere on E plane

图2 H平面非磁化等离子体球的双站RCSFig.2 Bistatic RCS of nonmagnetic plasma sphere on H plane

2 开槽钝锥体的RCS时域特性分析

在有些情况下，希望能在不改变目标空气动力学特性的同时增大目标的RCS，在钝锥体表面开适当的环槽并填充透波性能良好的材料可以达到这一目的。

采用 E(t)=exp［-4π(t-t0)2/τ2］表示的高斯脉冲入射到钝锥体上，对钝锥体的时域RCS特性进行分析。计算网格的剖分取Δx=Δy=Δz=δ，Δt=δ/2c，c为真空中的光速，脉宽取 τ=60Δt，得到钝锥体的后向远区时域响应如图3所示。

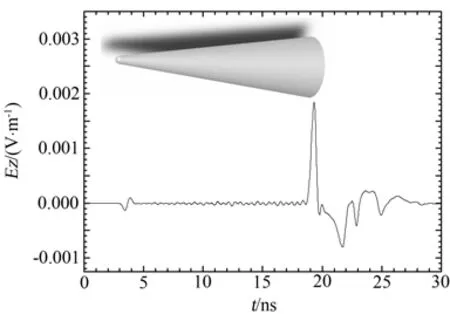
图3 钝锥体后向远区时域响应特性Fig.3 Far field time-domain backward response characteristics of blunt-cone

从钝锥体的后向远区时域响应图中可以看出，在钝锥体头部对应的位置有一个由镜面反射产生的较小回波，在锥底对应的位置有一个由边缘绕射产生的较大回波。因而可以判断出钝锥体的散射中心分别为头部和锥底，其中，锥底对钝锥后向RCS的影响比较大。

对图3所示的后向时域远场和入射脉冲分别作FFT变换，可以得到该钝锥体后向RCS随频率变化曲线，如图4所示。

图4 钝锥体后向RCS随入射波频率的变化Fig.4 Backscattering RCS of blunt-cone along incident frequency

下面分析开槽对钝锥体RCS时域特性的影响，钝锥模型开环槽的剖面图如图5所示。

图5 钝锥体开环槽剖面Fig.5 Section plane of the slot of blunt-cone

图6 比较了开槽前后钝锥体的时域响应特性的变化。从图中可见，在钝锥体表面开适当的环槽并填充透波性能良好的材料后，相当于增加了一个散射中心。其中，较高的峰为环槽反射和底部反射的叠加。对图6所示的后向远区时域响应曲线和入射脉冲分别作FFT变换，可以得到开槽和未开槽情况下钝锥RCS随频率变化曲线，如图7所示。

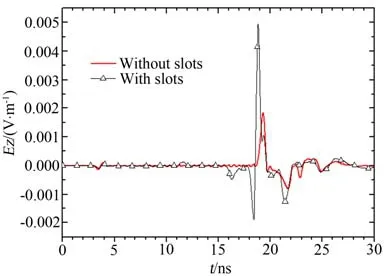
图6 开槽/未开槽钝锥体后向远区时域响应特性Fig.6 Far field time-domain backward response characteristics of blunt-cone with and without slot

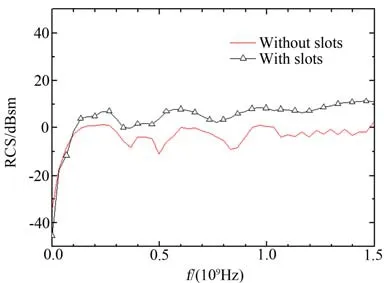
图7 开槽/未开槽钝锥体后向RCS随入射波频率的变化Fig.7 Backscattering RCS of blunt-cone with and without slot along incident frequency

从图7中可见，在钝锥体表面开适当的环槽并填充透波性能良好的材料时，在低频区和谐振区，入射波波长比环槽的尺寸大得多时，开槽后钝锥体RCS在原来RCS值的周围变化；而在高频段，钝锥体的RCS在很宽的范围内都增加了。

3 开槽钝锥体RCS试验与计算分析

为了分析开槽对钝锥体RCS的影响和验证计算方法，在中国空气动力研究与发展中心的气动物理靶上开展了开槽钝锥体RCS试验研究［9-10］，利用发展的RCS数值计算软件计算分析了试验模型在X波段和Ka波段下的RCS。

开槽钝锥试验模型底径12.0mm，长23.4mm，飞行速度5.4km/s，靶室(飞行环境)压强7.3kPa，电磁波从钝锥体头部入射并与飞行方向成60°夹角。图8是计算得到的试验条件下开槽钝锥模型绕流场等离子体鞘套的等离子体频率分布云图。当开槽钝锥体超高速飞行时，其驻点温度非常高，是飞行器表面防热材料的主要烧蚀区，开槽填充物质对等离子体流场的影响相对于驻点来说是小量，所以未考虑填充物质的烧蚀。

图8 等离子体鞘套的等离子体频率分布Fig.8 Distribution of plasma frequency of the flow field

在气动物理靶试验测量中，获得了钝锥体全目标RCS(包括等离子体鞘套和尾流流场)，雷达空间分辨率为2λ(λ为入射波波长)，可获得钝锥体及其尾迹RCS的一维空间分布，详细的试验测量结果见文献［10］，从测量结果中可分别获得钝锥体及尾迹的RCS。在弹道靶试验中，全目标RCS的绝大部分贡献来自目标本体及其等离子体鞘套的RCS，计算了等离子体包覆下开槽钝锥模型在X波段和Ka波段的双站RCS，并将计算结果与试验测量值进行了对比，如图9和图10所示。

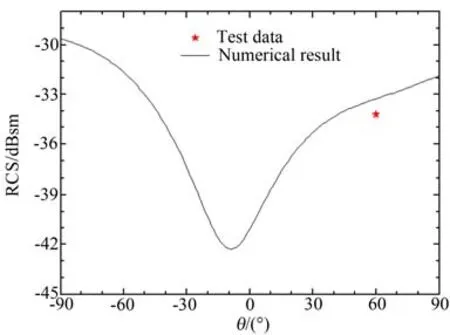
图9 开槽钝锥模型X波段双站RCSFig.9 Bistatic RCS of blunt-cone with slot at X band

X波段RCS计算值为-33.26dBsm，试验测量值为-34.50dBsm，二者相差0.94dBsm；Ka波段RCS计算值为-41.45dBsm，试验测量值为-42.40dBsm，二者相差0.95dBsm。通过数值计算和试验测量值的比较可以看出，无论是在X波段还是Ka波段，开槽钝锥模型RCS数值计算结果和试验测量值均符合较好。

对于目标探测，0°入射角(入射波从钝锥头部入射，方向与锥体轴向夹角为0°)附近是雷达的重点观测范围，下面分析当电磁波沿头部方向入射时，开槽前后RCS的变化情况。开槽和未开槽钝锥体X波段RCS对比结果如图11所示，可见在X波段开槽前后0°入射角附近RCS变化不大，这主要是由于X波段入射电磁波波长和槽的尺寸相比，处于低频区，因而相差不大。开槽和未开槽钝锥体Ka波段RCS对比结果如图12所示，在Ka波段，开槽后0°入射角附近RCS有较大程度的增加，这主要是由于开槽相当于增加了一个散射中心，此时入射波波长相对于槽的尺寸已经处于高频区，因而增加了钝锥体的RCS。

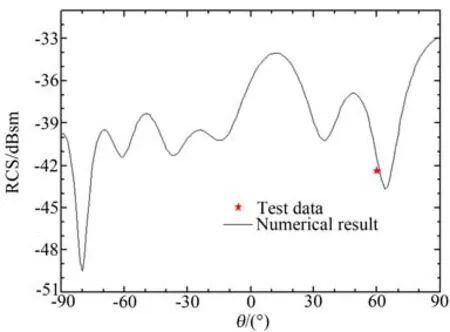
图10 开槽钝锥模型Ka波段双站RCSFig.10 Bistatic RCS of blunt-cone with slot at Ka band

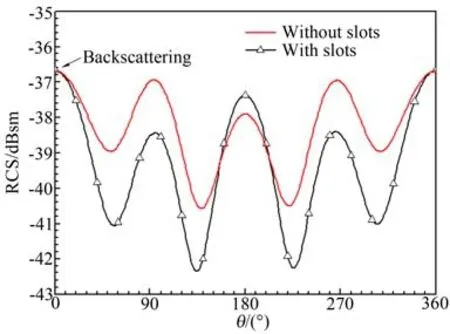
图11 开槽/未开槽钝锥体X波段双站RCSFig.11 Bistatic RCS of blunt-cone with and without slot at X band

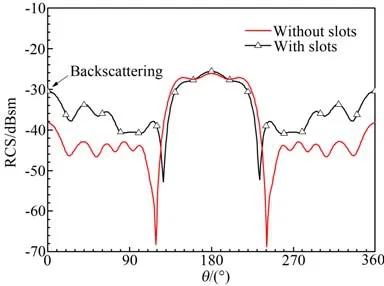
图12 开槽/未开槽钝锥体Ka波段双站RCSFig.12 Bistatic RCS of blunt-cone with and without slot at Ka band

4 结论

采用时域有限差分法(FDTD)研究了等离子体包覆目标的电磁散射特性，发展了超高速飞行器及其等离子体鞘套的RCS特性并行计算分析软件，计算分析了超高速开槽钝锥体的后向电磁散射远区时域特性和0°入射角附近的RCS特性，并进行了数值计算结果与试验数据的对比验证。研究结果表明，在钝锥体表面开环槽并填充透波性能良好的介质材料相当于在钝锥体表面人为地增加了一个散射中心，在低频区和谐振区，入射波波长比环槽的尺寸大得多或差不多时，开槽后钝锥体的RCS在原来RCS值的周围变化，而在高频区，钝锥体的RCS在0°入射角附近很宽的范围内都增大了。

致谢：中国空气动力研究与发展中心的董维中研究员为本文提供了流场计算数据，在此表示衷心的感谢。

［1］ 胡炜，周乐柱，祝西里，等.旋转对称金属目标上凹槽中填充材料对电磁散射影响的分析［J］.北京大学学报(自然科学版)，2004，40(3)：491-497.

［2］ YOUNG JL，NELSON R O.A summary and systematic analysis of FDTD algorithms for linearly dispersive media［J］.IEEE Trans.on Antennas and Propagat，2001，43(1)：61-77.

［3］ KELLEY D F，LUEBBERS R J.Piecewise linear recursive convolution for dispersive media using FDTD［J］.IEEE Trans.Antennas Propagat，1996，44(6)：792-797.

［4］ SULLIVAN D M.Z-transform theory and the FDTD method［J］.IEEE Trans.Antennas Propagat，1996，44：28-34.

［5］ YOUNG J L.A higher order FDTD method for EM propagation in collisionless cold plasma［J］.IEEE Trans.Antennas Propagat，1996，44：1283-1289.

［6］ 汤炜，闫玉波，李清亮.一种新时域交替隐式差分算法在散射问题中的应用［J］.物理学报，2004，53(12)：1473-4180.

［7］ 徐利军，刘少斌，袁乃昌.等离子体中的PLCDRC-ADIFDTD方法［J］.电子学报，2006，34(3)：483-486.

［8］ ZHANG Yu-qiang，GE De-biao.SARC-FDTD method for electromagnetic scattering by an object coated with plasma［J］.计算物理(英文版)，2010，27(6)：877-882.

［9］ ZENG Xue-jun，YU Zhe-feng，BU Shao-qing，et al.Research on the RCS of hypervelocity model and its plasma sheath［J］.空气动力学学报，2010，28(6)：645-649

［10］马平，部绍清，石安华，等.高超声速锥模型及其尾迹电磁散射实验研究［J］.实验流体力学，2010，24(4)：56-60.