双翼尖涡Rayleigh-Ludwieg不稳定性实验研究

刘志荣，朱 睿

(厦门大学航空系，福建厦门 361005)

0 引言

飞机尾流对飞行安全造成威胁，为了保证在机场终端区内飞机起飞、进场和着陆时的安全，国际民航组织在前后飞机之间规定最小尾流间隔标准。根据间隔标准，飞机在起飞/着陆时必须与之前的飞机保持安全距离，预留出足够的安全时间间隔，这就导致飞机起降频率降低［1］。为提高飞机安全性，同时改善机场的经济效益，如何对飞机尾迹涡进行控制并加快其消亡成为近年来民用航空领域中极具挑战性的研究课题。本实验以主动方式引入扰动，采用一种结构化矩形直机翼涡发生器触发一系列双翼尖涡Rayleigh-Ludwieg不稳定性，通过PIV系统测得双翼尖涡中主涡及次涡的运动特性、环量-时间特性，进行残余环量比例分析以说明双翼尖涡Rayleigh-Ludwieg不稳定性削弱翼尖涡强度之快速有效性［2-3］。

1 飞机翼尖涡消散机制

1.1 翼尖涡安全性危害分析

飞机翼尖涡形成之后具有很强的能量，短时间内不会消散，这对看不见的旋涡将会在一段时间内给后面的飞机带来安全隐患［4］。在两个旋涡的相互作用下，机身后形成了具有向上速度的区域(上洗区)和具有向下速度的区域(下洗区)，这样的速度分布使得后机在进入前机尾流场时，会产生不同程度的操纵困难甚至失控［5］。后机进入前机尾流场的情况可以大致分为4类情况，如图1所示。

图1 机身后尾流速度场及后机遭遇尾流情况Fig.1 Aircraft trailing vortexes velocity profile and aft-plane in-vortex status

1.2 翼尖涡Rayleigh-Ludwieg不稳定性

四涡系统是在两个翼尖涡中引入另外两个强度较小的涡，触发两个翼尖涡不稳定性的系统［6］。这种四涡系统，可以是引入两个分别与翼尖涡同向或反向的小涡，两个小涡分别与翼尖涡保持相应的距离，形成一个左右对称的系统，如图2、3所示。

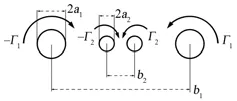
图2 同向四涡系统Fig.2 Codirectional rotation4-vortex system

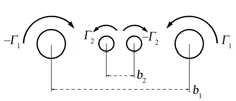
图3 反向四涡系统Fig.3 Opposite rotation 4-vortex system

机翼产生升力的原因可用Bernoulli方程解释为绕机翼环量Γ=∮u·d l不为零。对于无限长的二维机翼存在升力与环量的关系Fl=-ρU0Γ，而环量产生的起始必包含着把涡量排放到流体中的过程。根据Kelvin环量守恒定理，在空间必有一个闭合的回路以满足总环量为零。对于有限翼展大三维机翼来说，由于环量的存在，根据Stokes定理 (∮u·d l=∫ω·d s)，则意味着机翼附近一定涡量不断地产生，即翼尖涡。

以往的研究发现，采用与对应翼尖涡反向的小涡来诱导这种不稳定性所能达到的翼尖涡消散效果更为理想［7］。这种大小不同，方向相反，保持一定距离的涡之间所产生的缠绕、卷并等不稳定性叫做Rayleigh-Ludwieg不稳定性，它所描述的是两个反向涡之间交互作用下所产生的一系列现象［8］。在两涡Rayleigh-Ludwieg不稳定性的影响下，主涡将会被小涡剥离，产生相应程度的涡强度降低［9］。

2 流动显示实验系统

2.1 实验设备

实验测量工作在厦门大学航空系流体与PIV实验室中进行。该实验室现有多功能精密循环水槽系统(如图4所示)、PIV测速系统、天平测力系统。其中多功能精密循环水槽系统可以提供流场稳定的循环水流测试功能、台车拖动功能和造波功能，可用于流体力学中多领域的研究。PIV测试系统目前能满足二维流场的测量，将来将实现三维测量功能。六分量静态天平测力系统可以实现阻力、升力、侧力、滚转力矩、偏航力矩、俯仰力矩的测量。

图4 多功能精密循环水槽系统Fig.4 Multi-functional precision recycling water channel system

2.2 实验模型

实验模型是用来产生一对大小不同，方向相反的涡，而反向四涡系统又是一个关于中心竖轴对称的系统，因此在模型设计时可对其进行适当简化。实际实验中只考虑双涡系统，在理论上仍然能够产生Rayleigh-Ludwieg不稳定性。模型由3部分组成：主翼和小翼；用于安装主翼和小翼的大小两组夹具；前后两根连接支杆。

图5为实验模型安装方式，图6为实验模型。装夹着主翼、小翼的前后两根支杆可以任意固定在台车上的光学平板上，通过调节两个翼型的水平距离和旋转它们的角度得到不同间距b及不同强度Γ的翼尖涡组合［10］。实验模型所构成的双涡系统如图7所示，右侧主涡逆时针旋转，左侧次涡顺时针旋转，其强度分别为 Γ1、Γ2，间距为 b。

图5 实验模型安装方式Fig.5 Experimental model installation

图6 实验模型Fig.6 Experimental model

图7 双翼尖涡结构Fig.7 Dual trailing vortexes structure

2.3 双翼尖涡流动显示

调配合适的染色液进行流动显示实验，染色液能够保证良好的跟随性且在水中不易扩散［11］。实验中使用带有均匀小孔的圆柱管道来注入染色液，使染色液较均匀的位于观察截面上。这种注入染色液的方式能够使实验环境的干扰减少到最小程度［12］。翼型在穿过注有染色液的截面时，一方面由于翼尖涡的切向速度将带动截面上的染色液旋转，另一方面由于翼尖涡的轴向速度将拖动染色液粒子向翼型运动方向传播，形成一根完整的涡管。图8所示为染色液的注入和扩散。

图8 染色液注入与扩散Fig.8 Stain injection and diffusion

3 双翼尖涡流动显示实验

实验中染色液用量大致为每次70ml，台车速度设定为0.5m/s并保持不变。实验中调节的参数主要为主翼角度α1、小翼角度α2以及主翼和小翼之间的距离b。共进行11组实验，实验各参数如表1。

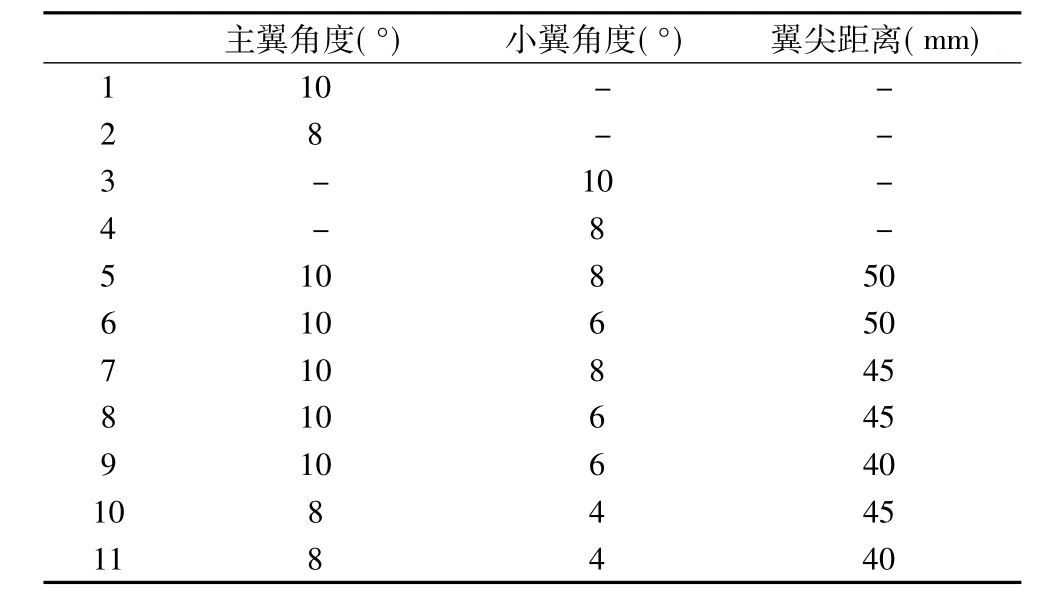
表1 实验参数组合Table 1 Experimental parameters combinations

3.1 双涡Rayleigh-Ludwieg特性分析

以主翼为10°、小翼8°、间距50mm参数组合为例，由图9和10可见两涡形成及相交过程。通过多组双涡流动显示实验，分析得到双涡Rayleigh-Ludwieg特性。

图9 两涡形成及相交(侧面)Fig.9 Dual vortexes formation and interaction(side vision)

图10 两涡形成及相交(端面)Fig.10 Dual vortexes formation and interaction(end vision)

(1)当在主涡旁的一定位置上引入另一个方向相反的次涡时，主涡不再保持在一个确定的位置上，它将在次涡的影响下往某个方向运动。其可能的运动路径与次涡位置、强度有很大的关系。当次涡和主涡的强度接近时，主涡和次涡会同时向下运动，这种情况类似于两个翼尖涡的下洗运动。而当次涡强度远小于主涡时，两涡则往主涡一侧运动。

(2)通过设置一定的主涡、次涡强度比Γ1/Γ2及其间距b，可获得双涡Rayleigh-Ludwieg不稳定性。通过实验可知要触发两涡Rayleigh-Ludwieg不稳定性，两涡间距及两涡强度比要合适。本实验条件下两涡相交不稳定性能够发生的实验参数组合为：b取40～50mm、主翼角度为10°～8°、小翼角度为4°～8°。

(3)在流动显示中，可以从侧面和端面来判断Rayleigh-Ludwieg不稳定性的发生。从侧面上看，次涡首先是被主涡拖动，绕其旋转方向运动，之后由于自身不稳定性而发生弯折，最后在绕主涡运动过程中被主涡拉近从而将主涡打散。从端面上看，主涡同次涡的运动路径将向主涡一侧移动，两涡下沉量很小，在两涡相交作用后主涡具有一定的向上运动趋势。

4 双翼尖涡PIV实验

4.1 PIV测量系统

PIV是一种基于光学显像的流体速度测量技术：在流体中加入随流体运动的示踪粒子，这些粒子在流经某一特定平面时被连续照亮两次，利用高速相机记录粒子瞬时流动，经图像处理可获得粒子在两次照亮时间差中的位移，从而得到流体速度场。

图11是PIV原理图。激光束通过片光光学元件形成具有一定厚度的片光照亮流场中特定区域，此时经过该区域跟随性及反光性良好的示踪粒子被照亮，通过CCD(CMOS)成像设备成像。该区域在一定时间间隔内通过脉冲激光连续照明两次，则可得到粒子在第一次照明时间t及第二次照明时间t'的两个流场视图，对这两个视图进行互相关分析就能得到流场内部二维速度矢量分布。

图11 粒子成像测速原理Fig.11 Particle image velocimetry

设流场中某一示踪粒子在二维平面上运动，其在x，y两个方向上的位移随时间的变化为x(t)、y(t)，则该示踪粒子所处流体质点的二维流速可以表示为：

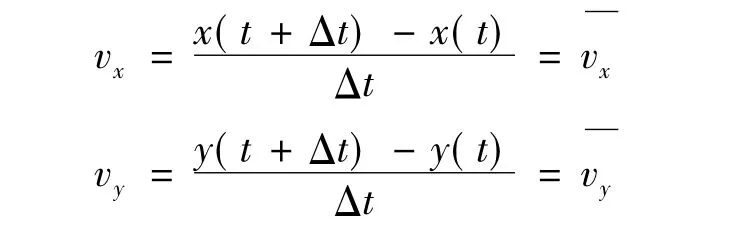
PIV系统硬件部分包括控制电路、CCD像机、光源、图像采集电路、图像采集计算机和同步信号计算机等；软件部分包括控制软件和分析软件，控制软件主要包括图像采集控制程序、同步程序以及比例标定程序，分析软件进行粒子图像处理和分析，并实现和修正流场速度矢量。

4.2 Rayleigh-Ludwieg不稳定性PIV实验

实验中拍摄区域基本包括了两涡运动的整个区域，调节采样频率为50Hz，设置相机光圈为最大值以保证采集图像质量。开始采集的时间先于台车启动时间，这是为能够准确确定两涡初始形成时间，台车速度调节为0.5m/s保持不变。选择不同的实验参数组合共进行18组双翼尖涡PIV实验。

以主翼为10°、小翼8°、间距50mm组合为例，经PIV系统测量、处理后得到各时刻(1s间隔)流场速度矢量图和流谱图(图12)。

t=0s时，两个矩形直机翼刚刚穿过激光片光面，主涡和次涡生成。在速度矢量图中，速度矢量越密集、长度越长则表明流场质点速度越大。由图可见两涡具有较大的核心速度，而越远离核心处速度越小，主涡速度及半径都大于次涡。流谱图显示主涡半径很大，主涡旋转速度带动右侧大部分流体绕主涡运动。

t=1s时，次涡绕主涡运动移动到了主涡的左下侧，同时次涡的速度有所减少。次涡绕主涡运动的趋势一直持续到t=5s，在这5s时间内，次涡在主涡的带动下运动，同时由于主涡的影响，次涡能量不断减少，速度逐渐减弱。次涡绕主涡运动的速度不是恒定不变，其运动速度先快后慢，且其形状会发生扭曲，应该是次涡在主涡拉力下产生的一种不稳定性。

t=6s时，从矢量图和流谱图上看，次涡涡心已经消失了，而主涡仍然比较稳定地存在。虽然次涡已不具完整性，但在次涡运动路径上仍有一部分逆时针旋转速度矢量，这部分矢量看似剩下的一半次涡，其与主涡旋转速度相反，并仍继续影响主涡。从速度矢量图上看，这部分矢量在绕主涡运动的过程中不断靠近主涡核心，使主涡的速度和能量有所减少。从t=6s到t=8s时间内，剩余的次涡矢量不断靠近主涡涡核，并试图改变其附近矢量的运动方向。t=9s时，次涡剩余矢量的能量几乎耗尽，此时主涡的涡心发生了明显的变形，同时主涡速度较0s时有明显的减少。

虽然t=9s时主涡涡心已经发生了变形，但由于主涡的能量还比较大，经一段时间后涡心又重新形成，但此时涡心速度已经比较小，说明主涡能量已经减少不小。t=13s时，涡心再次变形，Rayleigh-Ludwieg不稳定性使得主涡能量耗尽最终趋于消散。

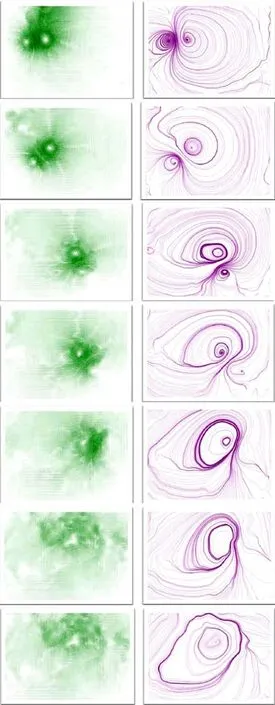
图12 双涡相交矢量图与流谱图Fig.12 Vectorgraph and flow pattern(Dual)

4.3 单涡PIV实验

以主翼10°时的流谱图为例，可见不同时刻测量截面的流体质点的运动情况。图13中可以看出旋涡形成后涡心很明显，靠近涡心处的流线是比较规整的圆形。图12与图13相比较可见，主涡在Rayleigh-Ludwieg不稳定性作用下在t=13s时其能量已大量削弱(图12)。当主涡以单涡形式发展时，在t=18s时刻其还依然保持较大的能量(图13)。可见Rayleigh-Ludwieg不稳定性削弱翼尖涡强度之快速有效性。

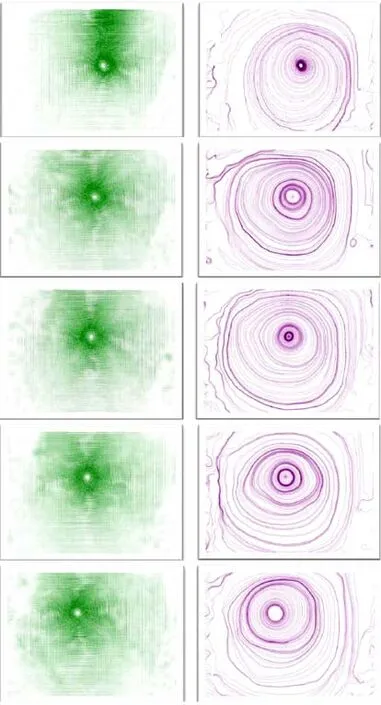
图13 单涡矢量图与流谱图Fig.13 Vectorgraph and flow pattern(Single)

4.4 双涡涡量图分析

速度场的旋度称为涡量，它是指流场中任何一点微团角速度之2倍，涡量通常用来量度涡旋的大小及方向。图14显示的是涡量的绝对值，因此主翼涡和小翼涡都显示为正值，但实际上主翼涡是逆时针旋转，小翼涡是顺时针旋转，因此主翼涡涡量应为正，小翼涡涡量则为负。云图中紫色部分涡量为0，红色部分涡量最大，从涡心开始往外涡量依次递减，这与速度矢量的大小变化一致。

5 双涡速度环量分析

在流场中任意一条封闭曲线，速度沿该封闭曲线的线积分称为该封闭曲线的速度环量，也形象地称速度环量为速度绕封闭曲线的速度功。速度环量的符号不仅决定于流场的速度方向，而且与封闭曲线的绕行方向有关，规定积分时逆时针绕行方向为正，即封闭曲线所包围的区域总在行进方向的左侧。二维封闭曲线的速度环量为：

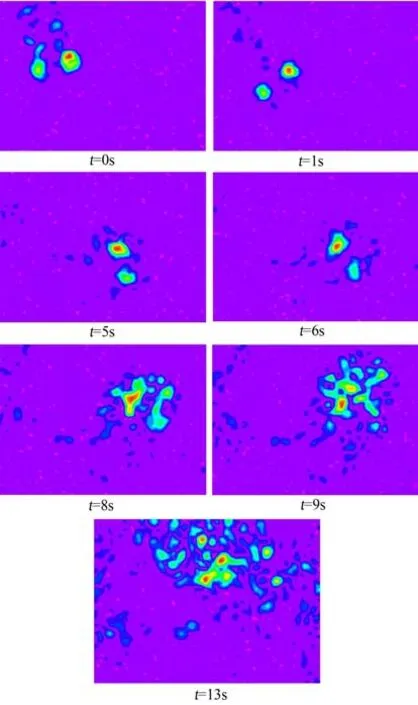
图14 双涡涡量图Fig.14 Dual vortexes vorticity

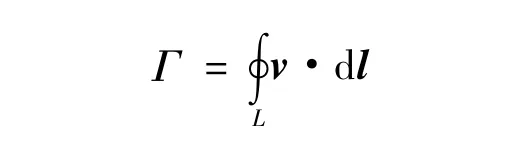
18组双翼尖涡PIV实验中，以每次实验0s时的环量为参考，其余时刻环量除以0s时刻环量得到不同时刻的特征环量，能够直观显示环量的减小比例。图15～图17为部分双翼尖涡PIV实验环量-时间图，对数据点进行线性拟合，通过比较环量-时间直线斜率，能够在一定程度上说明不同参数组合下的环量减小趋势。

由图可见，双翼尖涡相交消散效果最好的实验参数组合为主翼10°、小翼8°、间距50mm，其拟合直线斜率为-0.023；其次为主翼10°、小翼 6°、间距50mm，其拟合直线斜率为-0.020，这与流动显示实验中消散效果最好的参数组合一致。

图16 主翼10°次翼4°变间距环量-时间图Fig.16 The circulation-time figure of 10°，4°＆ variant b

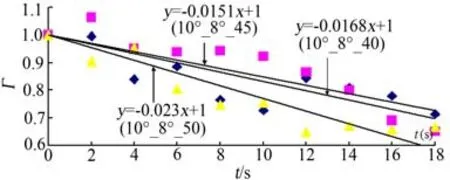
图17 主翼10°次翼8°变间距环量-时间图Fig.17 The circulation-time figure of 10°，8°＆ variant b

6 流场剩余环量比分析

取18s时刻翼尖涡环量除以0s时刻翼尖涡环量，可得流场剩余环量比，据其分析比较不同实验参数组合对双翼尖涡相交消散的影响。图18给出了不同角度组合在间距分别为40、45和50mm时的剩余环量比例。图中共有18个点，环量比大于0.85的共有5个，比例在0.7～0.85之间的共有4个，比例小于0.7的共有9个。由图可知，间距为50mm的环量比点相对集中于底部，即该间距的剩余环量比普遍较小，因此间距50mm为双翼尖涡相交消散最佳距离。

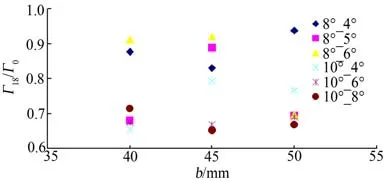
图18 剩余环量比与间距关系Fig.18 The relationships between residual circulation ratio and b

图19 所示为不同小翼角度α2下18组参数组合的流场剩余环量。由图可见，若只考虑小翼角度变化，则6°时剩余环量比普遍较小，4°时剩余环量比普遍较大，这与流动显示实验结论中的小翼角度过大或过小都不能较好地触发双翼尖涡Rayleigh-Ludwieg不稳定性相吻合。主翼角度变化同样影响剩余环量比，环量比大于0.8的点均来自主翼为8°时，因此可推断选择略大主翼角度有利于触发Rayleigh-Ludwieg不稳定性。如图，小翼8°时剩余环量比更小，因此选择主翼10°、小翼8°为双翼尖涡相交消散最佳翼角组合。双翼尖涡主涡与次涡强度比为Γ1/Γ2，研究不同Γ1/Γ2下翼尖涡强度削弱的特性，能够推断出最佳翼角组合以有效、快速地削弱涡强度。由图20可见，Γ1/Γ2处于1.3～1.4之间时，小于0.7的残余环量比点最多，故两涡强度比处于1.3～1.4时削弱效果较好。

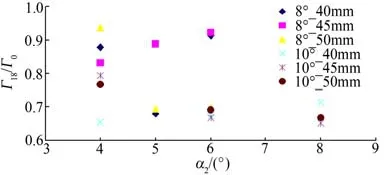
图19 剩余环量比与小翼角度关系Fig.19 The relationship of residual circulation ratio andα2

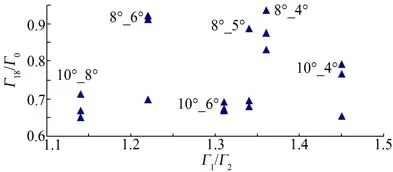
图20 剩余环量比与Γ1/Γ2关系Fig.20 The relationship of residual circulation ratio and Γ1/Γ2

7 结论

(1)当次涡和主涡的强度接近时，主涡和次涡会同时向下运动；而当次涡强度远小于主涡时，两涡则往主涡一侧运动。

(2)本实验系统中，两涡Rayleigh-Ludwieg不稳定性能够发生的条件为：b取40～50mm、主翼角度为10°～8°、小翼角度为4°～8°。

(3)双翼尖涡Rayleigh-Ludwieg不稳定性特征：次涡首先被主涡拖动，绕其旋转方向运动，之后由于自身不稳定性发生弯折，最后在绕主涡运动过程中被主涡拉近从而将主涡打散。

(4)双翼尖涡相交消散效果最好的实验参数组合为主翼10°、小翼8°、间距50mm，其拟合直线斜率为-0.023。

(5)间距50mm为双翼尖涡相交消散最佳距离；主翼10°、小翼8°为双翼尖涡相交消散最佳翼角组合。

(6)主涡与次涡强度比处于1.3～1.4时削弱效果较好。

［1］ BABIEB M，NELSON R C.The identification of an unstable wake vortex［J］.Journal of Flow Visualization and Image Processing，2009，16(2)：103-125.

［2］ BEARMAN P W.Understanding and predicting vortex-induced vibrations［J］.Journal of Fluid Mechanics，2009，634：1-4.

［3］ BABIE B M，NELSON R C.An experimental investigation of bending wave instability modes in a generic four-vortex wake［J］.Physics of Fluids，2010，22(7)：1-15.

［4］ LEWEKE T，WILLIAMSON C H K.Experiments on longwavelength instability and reconnection of a vortex pair［J］.Physics of Fluids，2011，23(2)：18.

［5］ ROY C，LEWEKE T，THOMPSON M C，et al.Experiments on the elliptic instability in vortex pairs with axial core flow［J］.Journal of Fluid Mechanics，2011，677：383-416.

［6］ RIEDINGER X，MEUNIERP，LE D S.Instability of a vertical columnar vortex in a stratified fluid［J］.Experiments in Fluids，2010，49(3)：673-681.

［7］ HEYES A L，TAYLOR N P，CHEN J.Characterising shortwave instabilities on a vortex dipole［J］.Experiments in Fluids，2011：1-9.

［8］ DONNADIEU C，ORTIZ S，CHOMAZ J M，et al.Threedimensional instabilities and transient growth of a counterrotating vortex pair［J］.Physics of Fluids，2009，21(9).

［9］ HARRIS D M，MILLER V A，WILLIAMSON C H K.A short wave instability caused by the approach of a vortex pair to a ground plane［J］.Physics of Fluids，2010，22(9).

［10］ BAO F，VOLHNERS H，HARTMUT M.Experimental study on controlling wake vortex in water towing tank［C］.ICIASF'03，Gottingen，Germany，2003.

［11］ BAO F，VOLLMERS H.Alleviation of end-effect in facilities for far wake investigations［C］.43rd AIAA Aerospace Sciences Meeting and Exhibit， Reno， Nevada， USA，2005.

［12］ BAO F，VOLLMERS.H.Experimental investigation of wake vortices with respect to end-effect in a water-towingtank［C］.STAB-DGLR Tagung，ZARM-Bremen，Germany，2004.