基于随机利率和通货膨胀的缴费确定型养老金计划最优资产配置策略

殷 俊，李媛媛

(武汉大学社会保障研究中心，湖北武汉 430072)

基于随机利率和通货膨胀的缴费确定型养老金计划最优资产配置策略

殷 俊，李媛媛

(武汉大学社会保障研究中心，湖北武汉 430072)

在随机利率和通货膨胀的背景条件下，应用随机动态规划方法，提出一个连续时间数学模型来分析动态资产组合选择，主要研究缴费确定型养老金计划的最优资产配置策略，旨在使其最终实际财富的期望效用最大化。用Cox–Ingersoll–Ross(CIR)过程来模拟名义利率的动态变化，用通货膨胀指数化债券来有效的对冲通货膨胀风险。通过应用随机动态规划方法，得出在CRRA效用函数下的最优资产配置策略。最后通过数值分析并计算出解析解来说明动态投资策略，可以帮助缴费确定型养老金计划的参与者建立自己的养老基金投资组合，根据其风险厌恶程度从现有的个人养老金产品中进行选择，并提出基于养老金受益人生命周期及不同风险偏好的投资策略。

缴费确定型;养老金;随机动态规划;资产配置;通货膨胀

一、引言和文献回顾

随着世界经济和社会的发展，社会养老保险制度在老年人的生活保障中发挥着越来越重要的作用，个人养老金的投资也得到广泛关注。在养老金计划的设计中，根据缴费和支付方式的不同，可以分为待遇确定型(Defined Benefit，DB)和缴费确定型(Defined Contribution，DC)计划。由于DB计划存在诸如供款与受益之间相关性较弱、难以与个人账户匹配等缺陷，DC计划在近年得到迅猛发展。在DC模式中，通常采用企业和个人共同缴费的方式，企业为每个计划参与者建立个人账户，进行账户式管理，个人账户资金采用完全积累的方式，投资收益计入职工个人账户。职工退休时可领取的养老金待遇就取决于缴费总额、缴费时间期限、基金投资组合收益等因素，而投资风险由职工个人承担。因此，资产配置策略对于DC型养老基金的管理是至关重要的。

一些早期的研究解决了在常数利率下，DC型养老金计划的最优资产配置问题，但忽视了通货膨胀的影响(Browne，Cairns et al，Gerrard et al)。［1－3］在有关最优资产配置的文献中，Vasicek［4］的 Ornstein－Uhlenbeck过程是描述利率动态变化过程的著名模型，该利率模型被用于Battocchio，Menoncin及很多早期的著作中，如 Sφrensen，［5］Brennan，Xia，［6］Boulier et al［7］。但 Vasicek 模型中的利率是分布式的，允许利率为负数，这不利于模拟名义利率的动态变化。Brennan，Schwartz，Lagnado［8］分析了基于债券、股票和现金三种资产的动态投资问题，他们假设短期利率、长期债券利率和股票的分红收益均服从马尔可夫过程，并证明考虑资产预期收益的策略将显著提高收益率。Brennan［9］研究了长期投资者的投资组合问题，研究表明不确定预期收益下，经过学习了的投资者风险资产配置比例的变化，变化的方向取决于对风险的容忍程度。Xia［10］基于连续时间模型证明了忽略预期和学习过程将大大提高投资者的机会成本。Battocchio，Menoncin［11］研究了在通货膨胀下DC型养老金资产的最优配置问题。

Grossman，Vila［12］探讨了若投资者的目标是财富不小于某个下限，如何进行最优资产配置的问题。Grauer，Hakansson［13］研究了通货膨胀对资产配置的影响，结论表明通货膨胀风险会明显改变投资者的资产配置决策。Campbell，Viceira［14］考虑的是最优消费－资产配置决策的递归效用投资者，无限投资期限，给出了近似解析解，他们认为若允许投资者投资于指数化债券，将会在很大程度上增加其效用。Menoncin［15］研究了养老金多阶段投资策略，考虑了多种背景风险，指出背景风险会影响投资者的财富水平，并且将随机通贷膨胀因素包含在各个因素中，Haberman，Vigna［16］采用随机动态规划方法研究了离散时间下的DC型养老金计划的最优投资策略，他们特别考虑了两种资产，即高风险资产和低风险资产，研究养老金受益人面临的向下风险，并考虑了不同风险厌恶的配置情况。Brennan，Xia［17］研究了动态投资组合最优化模型，模型将通货膨胀引入状态变量集中，认为多种因素共同影响和决定债券价格，这里通货膨胀作为影响长期债券的状态变量。Boulier et al，［7］Deelstra et al［18］用鞅方法解决了受保护的DC计划的最优资产配置问题。Battocchio，Menoncin，Scaillet［19］假设金融市场中存在一种无风险资产和n种价格服从对数正态分布的风险资产，基于养老金受益人的随机死亡时间，求解当CRRA效用最大化时的资产配置问题，并考虑了养老金的累积和给付阶段，结论是最优配置在第一阶段风险资产的比例越来越小，而第二阶段则越来越大。Munk，Sorensen［20］讨论了投资者投资于现金债券和股票市场，目标是期末效用最大化的模型，他们考虑了利率和通贷膨胀的风险因素对投资者资产配置决策的影响。Battocchio，Menoncin，Gao采用随机动态规划方法解决了连续时间下DC养老金计划的最优投资组合管理问题。在 Battocchio，Menoncin［11］的研究中，假定利率、供款流向及通货膨胀率是随机的，但没有考虑对最终财富的最低担保问题。Gao［21］应用勒让德变换解决了DC计划的动态规划问题，但忽视了通货膨胀风险与最低担保问题，而且假定缴费率是确定性的。

李珍［22］对养老金多元化投资和入市的重要性、多元化投资工具以及入市的途径和规模等问题进行了一定探讨。李耀［23］提出了一个考虑发起企业的经营活动现金回报率的年金组合理论模型，分析了当前我国行业年金、地方企业年金以及保险公司经办年金等三类年金的投资组合情况，并提出了相关政策建议。徐静和张波［24］考虑了连续时间下的待遇确定型养老金模型的最优控制问题，在养老金期望给付为指数增长、目标函数为最小化贡献率风险和偿付能力风险线性组合的假设下，得到了无风险投资时的最优贡献率和最小风险。叶燕程和高随祥［25］利用随机控制理论研究缴费确定型企业年金最优投资策略分别在固定缴费和随机缴费情形下，建立基于给付损失最小化的企业年金最优投资模型，通过求解HJB方程得到最优投资策略和给付水平显式解，并对固定缴费时的最优策略进行蒙特卡洛仿真模拟。肖建武，翟红，秦成林［26］对常方差弹性模型下退休前和退休后两个阶段进行了投资策略研究，目标是使最终期望财富效用函数最大化，利用随机控制理论得到HJB方程，运用勒让德变换理论及对偶方法求解方程得到退休前和退休后两个时期的最优风险资产的投资数额。郭磊和陈方正［27］在常数相对风险规避效用函数的假定下，构建了企业年金计划退休前有固定投入，退休后有固定支出的连续时间随机动态规划模型，求出了退休前和退休后的最优投资策略。

本文延伸了 Boulier et al，Deelstra et al，Battocchio，Menoncin之前的研究。在 Boulier et al与Deelstra et al的研究中，考虑在DC型养老金计划中采用最低收益率担保，但忽视了通货膨胀风险。Battocchio，Menoncin考虑了通货膨胀风险对最优DC型养老金计划的影响，但其模型中没有引入最低收益率担保，且经济中未包含通货膨胀指数化债券。因此，本文基于随机利率和通货膨胀，提出一个连续时间数学模型来分析动态资产组合选择，主要研究DC型养老金计划的最优资产配置问题。研究的思路和框架为:首先，用Cox–Ingersoll–Ross(CIR)过程来模拟名义利率的动态变化，CIR模型是Cox，Ingersoll，Ross［28］提出的，该模型在 Vasicek 模型的基础上进行了改进，模型资产价格及其随机特性都是内生确定的，依赖于真实经济变量，基本假定是每个投资者都通过对单一商品的选取达到预期效用最大化，模型利用理性的资产定价模型研究利率期限结构，进一步把期限结构理论推广到一般均衡的环境中去。模型考虑了风险偏好、时间偏好、财务限制、风险补偿等因素。该模型的最重要优点是不允许出现负利率，这对于模拟名义利率来说是更符合实际的假定。其次，假定瞬时的通货膨胀遵循一个扩散过程，通货膨胀率及利率与股票收益部分相关。为了避免DC型养老金计划出现基金短缺，有各种类型的最终收益担保。本文假定在退休时，有一个与通货膨胀指数化年金数量挂钩的最低保证金，这有助于年金受益人对冲通货膨胀风险。由于指数化年金的价值可被视为指数化附息票债券，因此，担保的价值是随机的，因退休时的利率和价格水平而异。

二、理论分析框架及实证模型设定

假定DC型养老金计划的参与者可将他们的资金投资于现金账户(货币市场基金)、名义债券基金、股票指数基金以及通货膨胀指数化债券基金。该优化问题旨在使计划参与者在退休时的期望效用最大化。本文假定利率、供款流向、通货膨胀率及最低收益担保是随机变化的。在最低收益担保的约束下，常数相对风险厌恶参与者的最优资产配置策略可由闭合表达式推导出。

(一)金融市场结构模型

金融市场的第一种资产为现金账户Mt，可以得出下式:

式中，Rt是瞬时名义无风险利率，假定Rt遵循平方根CIR过程:

式中，a，b为常数，σR为利率的波动率，Z1t是标准布朗运动，CIR过程不允许出现负Rt，这种非负特性在模拟名义利率时非常重要。若2a≥σ2R，瞬时利率对所有t＞0都有严格正实性。

金融市场的第二种资产为名义零息债券。令B(t，T)表示在到期时名义回报为1$且期限为T的名义零息债券在t时刻的价格。利率风险的市场价格由λR给定并且无套利，B(t，T)可从边界条件为B(T，T)=1的偏微分方程中求出，如下式:

式中，BR与BRR代表B关于R的一阶与二阶偏导数。B(t，T)的解由如下显式公式得出:

正如Boulier et al.的研究中所讨论的，个人不可能在经济中找到所有的零息债券，为了方便起见，我们在分析中引入一个固定期限为T1的滚动债券。该滚动债券的动态方程如下式:

式中，Z2t是独立于Z1t的标准布朗运动，λS表示相对于dZ2t的风险的市场价格。一揽子商品的名义价格水平由Pt表示，Pt的动态方程由如下随机微分方程给出:

式中，π是预期通货膨胀率，Z3t是独立于Z1t与Z2t的布朗运动，它代表除利率风险和股票市场风险之外的非系统风险。

金融市场中的第四种资产是通货膨胀指数化零息债券。该指数债券在到期日T确定支付PT。指数债券的价格I(t，T)由如下以边界条件为I(T，T)=PT的偏微分方程决定:

式中，λP表示相对于dZ3t的风险的市场价格。I(t，T)的显式解为:

式中，σI2≡σP2且σI3≡σP3。同时假定市场中交易的指数化债券是固定期限为τ2的滚动指数化债券:

(二)最优化问题

在确定缴费型养老金计划中，参与者在退休日T之前将持续缴费。用Ct表示瞬时缴费率，在完全市场假设下，Ct满足以下随机微分方程:

对于最终养老金待遇的担保问题，我们假定最终待遇可转换成具有下行保护的终身年金。根据一揽子商品来确定实际最低年金g，一揽子商品在t时刻的价格为Pt，该年金的名义价值为gPt，∀t∈［T，T'］，其中T'表示死亡日期。在时间T担保水平的名义价值是一个指数化息票债券的价值，定义为:

由于I(T，s)取决于在s≥T条件下的RT与PT的价值，担保水平GT取决于最终实现的RT与PT的值。让Wt表示t时刻退休账户的财富，W0为财富的初始值。DC计划参与者将其账户中的财富投资于金融市场，目标是使最终的实际财富超过最低收益担保的期望效用最大化。参与者的最优化问题可以描述如下:

参与者的偏好由CRRA效用方程代表，γ是相对风险规避的程度。式(27)中，xBt，xSt，xIt分别为t时刻投资于名义零息债券、股票与指数化债券的投资组合权重。因此，投资于现金账户的基金财富比例为1－xBt－xSt－xIt。式(28)中，Λ为风险的市场价格向量，式(29)中，Γ是因子负荷矩阵。

(三)模型参数设定

表1列出了表征金融市场的各项参数，假定积累阶段为40年，年金给付阶段为20年，对年金g的担保水平为g=10，相对风险规避系数为γ=2。

表1 模型的参数值

三、最优化问题的解决方案

(一)变换初始问题

通过运用变量变化的方法，受保护的DC型养老金计划的最优资产配置问题，可以由最初的非自筹资金并受最低收益担保约束的问题转换为自筹资金且无约束的问题。在这种情况下，我们很容易在模型中运用标准随机动态规划方法去寻找最优投资规则的显式解。

首先，在完全市场及无套利的假设条件下，我们构建一个假定的金融工具，在s时刻的瞬时供款为CS。该假定的资产在t时刻(t≤s)的价值由D(t，s)表示，且D(t，s)必须满足下列边界条件为D(s，s)=CS的偏微分方程:

容易证明D(t，s)满足下列随机微分方程:

其次，我们定义一个新过程Ft:

实际上，Ft代表假定的息票债券的价值，其瞬时票面利率为Ct，相当于从时间t到T的未来供款的现值。Ft收益的动态方程为:

即使Ft不直接在金融市场中交易，Ft的收益由金融市场中可交易资产的投资组合所复制:

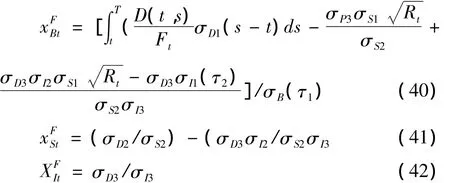
我们定义Gt为t时刻最低收益担保GT的现值，如下:

这表明，Gt的动态变化可由金融市场中交易的资产所复制。与该复制性投资组合的关系如下:

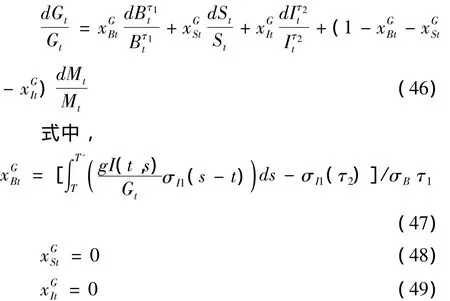
最终担保的复制性投资组合由名义与指数化债券组成，而与股票不相关。该复制性投资组合中指数化债券的权重为100%，是常数。这意味着指数化债券是复制退休时担保水平的主要组成部分。上文提到，担保可被视为指数化息票债券。由于仅有一个固定期限的指数化零息债券在金融市场中交易，该复制性投资组合中的名义零点旨在调整指数化零息债券的期限与指数化息票债券的期限相匹配。由于投资于指数化债券的财富比例为100%，则投资于名义债券的财富比例以短期利率融资。

在Ft与Gt的帮助下，我们可将最初的非自筹资金的约束问题转换成一个自筹资金的无约束问题。由此，可定义一个盈余过程Yt如下:

Yt的动态变化过程如下式:

将式(26)、(37)、(44)代入上面的等式得:

由定义，Yt≡WT+FT－ GT=WT－ GT，初始的最优化问题可转换为根据盈余过程的无约束的自筹资金投资问题:

(二)无约束问题的解决方案

我们应用随机动态规划方法去解决式(54)定义的最优化问题。定义最优化问题的价值函数为J(Yt，Rt，t，T):

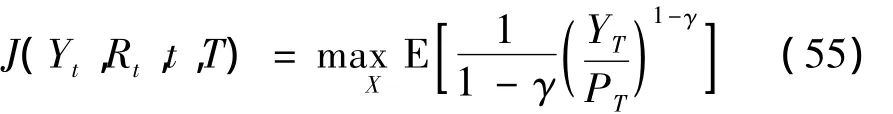
式中 Et［·］E［· /Ft］，Ft是由{(Z1S，Z2S，Z3S:0≤s≤t}生成的σ域。由最优性原则得到Hamilton–Jacobi–Bellman(HJB)方程:

当价值函数J(·)的解给定时，该无约束问题的最优投资组合策略可相应解决:

无约束投资组合的第一部分是对风险资产的短视或投机需求。这部分需求符合从传统的均值－方差分析得出的结论。投资者持有短视的投资组合，为了获得风险溢价，短视需求与投资者的风险规避系数成反比。无约束投资组合的第二部分是对风险资产的对冲需求。式(58)中，对冲利率风险的资产为名义债券，因为它与名义利率的变化是完全负相关的。无约束投资组合的最后一部分用于对冲通货膨胀风险。这部分由持有多头头寸的指数化债券及持有空头头寸的名义债券组成。该部分中指数化债券的需求为财富的100%，这意味着指数化债券在对冲通货膨胀风险时起着重要的作用。名义债券持有空头头寸说明，由于指数化债券的收益也与名义利率相关，则名义债券可被指数化债券部分替代。

(三)初始问题的解决方案

具有中期供款流向和最终通货膨胀指数担保的最优投资策略可由下式得到:

最优投资组合是三个不同部分的加权平均值。第一部分是上文得出的无约束投资组合。第二部分是复制了中期供款流向现值的投资组合。第三部分是复制了最终担保水平的现值。由式(60)推导出的最优投资组合权重取决于状态变量 Wt，Yt，Ft，Gt的实现。下一部分通过数值应用来描述动态投资组合策略的特征。

四、随机利率及通货膨胀下的资产配置模型求解与分析

(一)有最低收益担保的情况

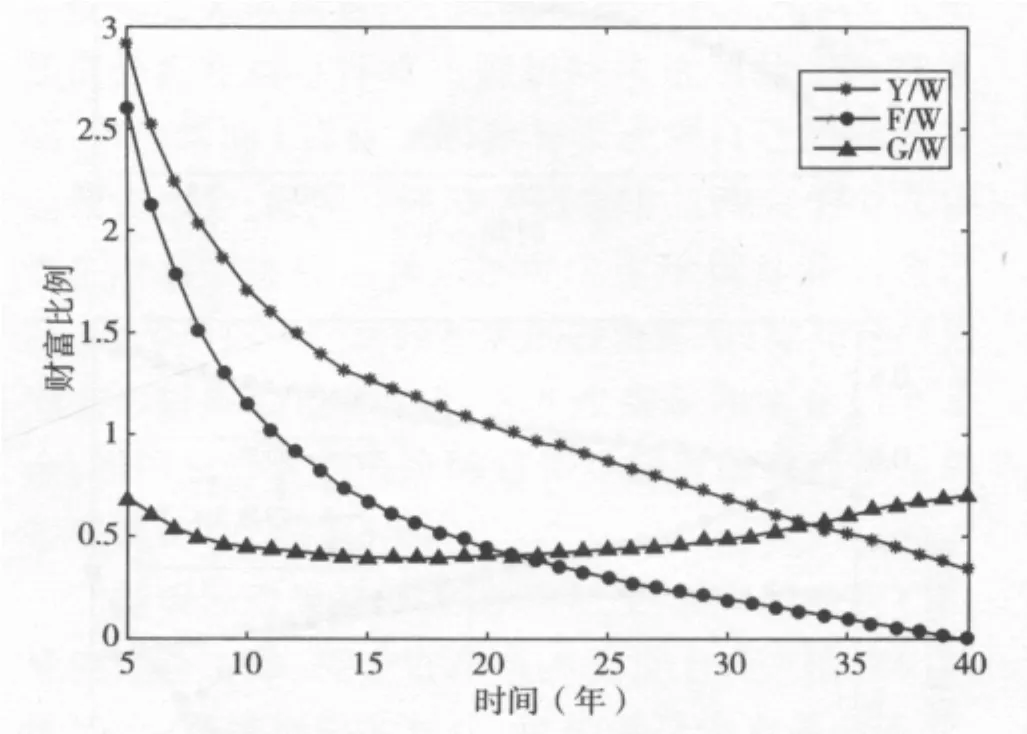
图1 Yt，Ft，Gt占 Wt的比例

根据设定的模型及参数值，运用上文提出的最优化问题的解决方案，利用MATLAB软件对该模型进行数值模拟，探讨在不同条件下，确定缴费型养老金计划的最优资产配置策略。图1显示了Yt，Ft，Gt在总基金财富Wt中所占的比例。在积累阶段初期，未来供款流向的现值Ft较高，而担保水平的现值Gt相对于总基金财富Wt较低。这使得基金的盈余Yt相对于基金财富较高，因为Yt≡Wt+Ft－Gt。当临近退休时，Yt/Wt及Ft/Wt下降而Gt/Wt上升。

图2(上)显示了最优投资组合权重从t=5到t=40的变化过程。在积累阶段初期，DC计划参与者追求基金财富的增长，因此大量投资于风险资产。投资于名义债券与股票的财富比例最初较高，但随时间逐渐降低，分别从初始值2.09与1.84降至 －0.06与0.32。投资于指数化债券与现金的财富比例最初较低，但随时间逐渐增加。投资于指数化债券的比例从 －1.25增至0.64，投资于现金的比例从－1.68增至0.10。如图1所示，由于在积累阶段初期的约束较为宽松，盈余 /财富比(Yt/Wt)较高，参与者可采用较为激进的投资策略来促进基金的增长。相反，当逐渐接近退休日期时，上升的Gt/Wt比率促使参与者将基金财富转向安全的资产。

图2 股票、名义债券、指数化债券及现金的最优投资组合权重① 图2中，T=40，T'=60，g=10，左图与右图的相对风险规避系数分别为γ=2与γ=5。

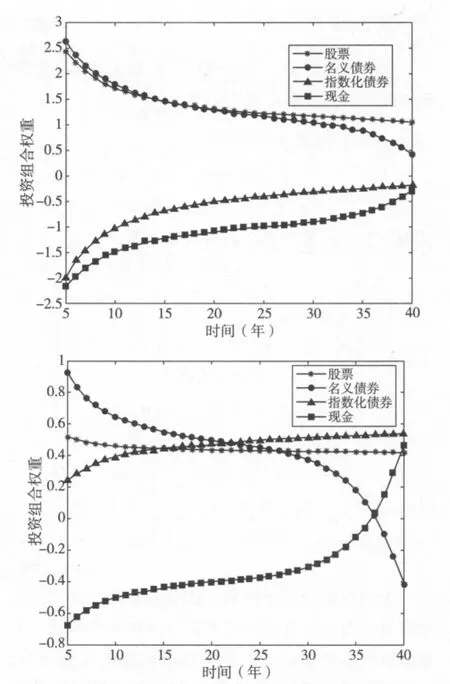
图3 股票、名义债券、指数化债券及现金的最优投资组合权重② 图3中，T=40，T'=60，g=0，左图与右图的相对风险规避系数分别为γ=2与γ=5。

为了进行比较，我们模拟了一个受保护的养老基金的投资组合策略，其具有较高的风险规避系数γ=5，如图2(下)所示。投资于名义债券与股票的财富比例最初较高，但随时间逐渐下降，名义债券从0.69 降至 － 0.31，股票从0.27 降至0.12。投资于指数化债券与现金的财富比例在临近退休时逐渐增加，指数化债券从0.52 增至0.86，现金从 － 0.48 增至0.33。当γ=5时，通货膨胀指数化债券从t=8开始在基金投资组合中占有主要地位，比γ=2的情况早了很多。指数化债券与现金的组合权重大大高于前者，而风险资产(股票与名义债券)的组合权重则比前者更低。

这两个例子的区别源于无约束投资组合的套期保值需求。根据式(58)，当风险规避系数γ较高时，投机性的投资减少，从而减少了对股票的需求。另一方面，高风险规避系数增加了名义债券与指数化债券的投资组合权重，以分别对冲利率风险与通货膨胀风险。然而，增加的指数化债券的对冲需求将部分替代对名义债券的投资，因为指数化债券的收益与瞬时利率负相关。这就解释了为什么风险规避系数大的名义债券所占投资组合权重比风险规避系数小的名义债券所占权重低的原因。

(二)无最低收益担保的情况

在DC型养老金计划不受保护的情况下，g=0，我们重新计算上例的结果。图3(上)与图3(下)分别显示了当γ=2与γ=5时，且无最低收益担保的情况下，最优投资组合的权重。该投资组合变化的主要特点类似于受保护情况下的投资组合，股票与债券所占权重最初较高，在临近退休时逐渐减少。当γ =2时，股票所占的组合权重从2.44降至1.03，名义债券从2.63降至0.43;当γ=5时，股票所占的组合权重从0.51降至0.41，名义债券从0.92降至－0.42。指数化债券与现金所占的权重随着时间推移而不断上升。当γ=2时，指数化债券所占权重从－ 1.93 升至 － 0.16，现金从 － 2.14升至 － 0.30;当γ =5时，指数化债券所占权重从0.24升至0.53，现金从 －0.67升至0.47。由此可见，在无最低收益担保的情况下，当γ=5时，从t=22开始，指数化债券在养老金投资组合中仍占有主导地位。图3表明，只有无约束的投资者并且其风险厌恶程度较低，如γ=2，会在整个积累阶段持有指数化债券空头头寸。从经验上看，对指数化债券有一个负通货膨胀风险溢价，指数化债券可规避不确定的通货膨胀风险，因此一个风险厌恶程度较低的投资者将持有指数化债券的空头头寸以获得通货膨胀风险溢价。在数值应用中得到的结果一致表明，除了低风险厌恶程度的无约束的投资者之外，指数化债券被证明是在养老金投资组合中最主要的资产，尤其是在积累阶段的后期。

五、结论与启示

本文主要研究缴费确定型养老金计划的最优投资组合策略，旨在使其最终实际财富的期望效用最大化。假定利率、供款流向、通货膨胀率都是随机变化的。在年金化阶段给付的年金被假定是与通货膨胀指数挂钩的，以保护年金受益人退休后的购买力。同时，也考虑了对年金的最低收益担保问题。除了传统的资产类别，如现金、股票及名义债券，金融市场还包括通货膨胀指数化债券，使得DC计划参与者能建立一个投资组合，实现对通货膨胀指数化年金的担保，同时也帮助参与者在积累阶段对冲通货膨胀风险。在风险规避系数较高或提供了下行保护的情况下，养老金投资组合应集中投资于指数化债券，而不是其他的风险资产。通货膨胀指数化债券对于养老金计划对冲通货膨胀风险以及为年金受益人提供下行保护是必不可少的。因此，通货膨胀指数化基金的发行以及通货膨胀指数化债券市场的发展有助于养老基金行业的健全与完善。

通过运用变量变化的方法，受保护的DC型养老金计划的最优资产配置问题，可由最初的非自筹资金并受最低收益担保约束的问题转换为自筹资金且无约束的问题。通过应用随机动态规划方法，我们得出了在CRRA效用函数下的最优资产配置策略。结果表明，股票与名义债券所占的权重最初较高，随着时间的推移而逐渐下降;通货膨胀指数化债券与现金所占权重最初较低，随着时间的推移而逐渐增加。与早期没有包含指数化债券的研究相比，通货膨胀指数化债券在风险厌恶的DC计划参与者的养老金投资组合中占有主导地位，这反映了在到期时提供一定实际收益的指数化债券，从长远来看是仅有的无风险资产(扣除物价因素)。本文应用数值分析并通过计算出解析解来说明动态投资策略，可以帮助DC计划的参与者建立自己的养老基金投资组合，根据其风险厌恶程度从现有的个人养老金产品中进行选择。还可应用于设计养老金产品，给客户提供与年龄相关的投资策略，比如专门为养老理财规划设计的生活方式基金和生命周期基金，根据投资者的风险偏好和年龄自动改变基金的投资风格和投资组合。

随着风险规避系数的增大，投资于风险资产的比例显著下降，现金资产所占比重上升。随着年龄的增大，投资期限的减小，风险承受能力逐渐降低，投资于风险资产的比例应越来越低。总而言之，宏观经济是影响养老金资产配置的重要因素，通过本文建立的模型，能够有效地对资产进行最优配置，使养老金投资人受益。

［1］Browne S.Beating a moving target:Optimal portfolio strategies for outperforming a stochastic benchmark［J］.Finance and Stochastics，1999，3:275 –294.

［2］Cairns A，Blake D，Dowd K.Stochastic lifestyling:Optimal dynamic asset allocation for defined contribution pension plans［J］.Journal of Economic Dynamics and Control，2006，30:843–877.

［3］Gerrard R，Harberman S，Vigna E.Optimal investment choices post－retirement in a defined contribution pension scheme［J］.Insurance:Mathematics and Economics，2004，35:321–342.

［4］Vasicek O.An equilibrium characterization of the term structure［J］.Journal of Financial Economics，1977，5:177–188.

［5］S∅rensen C.Dynamic asset allocation and fixed income management［J］.Journal of Financial and Quantitative A－nalysis，1999，34:513–531.

［6］Brennan M J，Xia Y.Stochastic interest rates and the bond － stock mix［J］.European Finance Review，2000，4:197–210.

［7］Boulier J F，Huang S J，Taillard G.Optimal management under stochastic interest rates:the case of a protected defined contribution pension fund［J］.Insurance:Mathematics and Economics，2001，28:173–189.

［8］Brennan M J，Schwartz E S，Lagnado R.Strategic asset allocation［J］.Journal of Economic Dynamics and Control，1997，21:137 －140.

［9］Breanan M J.The role of learning in dynamic portfolio decisions［J］.European Economic Review，1998，1:295－306.

［10］Xia Y.Learning about predictability:The effects of parameter uncertainty on dynamic asset allocation［J］.Journal of Finance，2000，56:585－594.

［11］Battocchio P，Menoncin F.Optimal pension management in a stochastic framework［J］.Insurance:Mathematics and Economics，2004，34:79–95.

［12］Grossman S J，Vila J L.Portfolio insurance in complete markets:A note［J］.The Journal of Business，1989，19:473－478.

［13］Grauer R，Hakansson N.On timing the market:The empirical probability assessment approach with an inflation adapter in worldwide asset and liability modeling［M］.Cambridge University Press，1998:149－181.

［14］Campbell J Y，Viceira L M.Who should buy long term bonds?［J］.American Economic Review，2001，91:99–127.

［15］Menoncin F.Optimal portfolio and background risk:An exact and an approximated solution［J］.Insurance:Mathematics and Economics，2002，31:249－265.

［16］Haberman S，Vigna E.Optimal investment strategies and risk measures in defined contribution pension schemes［J］.Insurance:Mathematics and Economics，2002，31:35–69.

［17］Brennan M J，Xia Y.Dynamic asset allocation under inflation［J］.Journal of Finance，2002，57:1201 –1238.

［18］Deelstra G，Grasselli M，Koehl P F.Optimal investment strategies in the presence of a minimum guarantee［J］.Insurance:Mathematics and Economics，2003，33:189–207.

［19］Battocchio P，Menoncin F，Scaillet Q.Optimal asset allocation for pension funds under mortality risk during the accumulation and decumulation phases［R］.FAME Discussion Paper No，66，2003.

［20］Munk C，S∅rensen C，Vinther T N.Dynamic asset allocation under mean－reverting returns，stochastic interest rates and inflation uncertainty are popular recommendations consistent with rational behavior?［J］.International Review of Economics and Finance，2004，13:141–166.

［21］Gao J.Stochastic optimal control of DC pension funds［J］.Insurance:Mathematics and Economics，2008，42:1159–1164.

［22］李珍，刘子兰.我国养老基金多元化投资问题研究［J］.中国软科学，2001(10):4 －8.

［23］李耀.企业年金基金投资:基于理论模型和实践经验的研究［J］.商业经济与管理，2007(1):46－51.

［24］徐静，张波.给付确定型养老金计划的动态最优控制［J］.自然科学进展，2006，16(9):1174 －1180.

［25］叶燕程，高随祥.缴费确定型企业年金最优投资策略研究［J］.中国科学院研究生院学报，2007，24(2):149－153.

［26］Xiao J W，Zhai H，Qin C L.The constant elasticity of variance(CEV)model and the legendre transform －dual solution for annuity contracts［J］.Insurance:Mathematics and Economics，2007，40:302 －310.

［27］郭磊，陈方正.基于CRRA效用函数的企业年金最优个体投资策略［J］.同济大学学报(自然科学版)，2008，36(3):424 －426.

［28］Cox J C，Ingersoll J E，Ross S A.A theory of the term structure of interest rates［J］.Econometrica，1985，53:385－407.

Stochastic Interest Rate and Inflation Based Optimal Asset Allocation Tactics for Defined-Contribution Pension Plans

YIN Jun，LI Yuan－yuan
(Center for Social Security Studies of Wuhan University，Wuhan 430072，China)

In this paper，we propose a continuous－time mathematical model by using the stochastic dynamic programming approach under the background of stochastic interest rate and inflation to study the optimal asset allocation for a defined－contribution pension plan to maximize the expected utility of its terminal real wealth.The dynamic changes of nominal interest rate are simulated by the Cox－Ingersoll－Ross process.In order to hedge against the inflation risk more efficiently，the inflation－indexed bonds are used .The stochastic dynamic programming approach can be used to find the optimal asset allocation tactics in CRRA utility function.Finally，this paper helps the participants of defined－contribution pension plan build their own pension investment portfolio and choose from the current individual pension products according to their risk aversion by numerical value analysis and calculating resolution solution to explain dynastic investment tactics and raises the investment tactics based on the life cycle and different risk aversion of pension beneficiaries.

Defined－Contribution;Pension;Stochastic Dynamic Programming;Asset Allocation;Inflation

A

1002－2848－2013(02)－0011－10

2013－01－08

教育部人文社会科学重点研究基地重大项目《社会保障精算研究》，项目负责人:殷俊，项目编号:11JJD840017。

殷俊(1962－)，湖北省武汉市人，管理学博士，教授，博士生导师，武汉大学社会保障研究中心(国家人文社会科学重点研究基地)专职研究员，国家“985工程”科技创新平台和哲学社会科学创新基地核心成员，研究方向:社会保险与金融投资;李媛媛(1984－)女，新疆维吾尔自治区乌鲁木齐市人，武汉大学社会保障研究中心博士研究生，研究方向:社会保障基金投资与管理。

责任编辑、校对:郭燕庆