外周听觉系统对声音的表达

周晓正， 周骏拓

1.北京石油化工学院信息工程学院,北京 102617；

2.北京大学基础医学院，北京 100191

引 言

自然事物在发生、发展过程中往往伴随着声波的产生，声波的性质也因此反映出自然事物的性质。因此，人类及很多动物都逐渐进化出了专门识别声波的听觉系统，通过感知声波来间接感知周围环境的变化。经过几十年的研究，人们对听觉系统的整体结构及神经通路有了较深入的了解，尤其是对听觉外周系统，人们在生理学实验、理论建模及工程应用等方面都取得了显著成绩。早在1928年，就有人在动物耳蜗基底膜实验中发现声波是以行波方式沿基底膜传播的[1,2]。随着Mossbauer技术的出现，人们可以在生理状态良好的活体耳蜗上对基底膜的特性进行较为准确的测量。在这方面比较有代表性的是Rhode等人[3～6]对基底膜的系列测量实验。利用微电极技术可以实现单根听神经纤维电位的精确测量，使得人们能够对听觉系统各层次上的神经纤维对于各种声音刺激的编码机制进行定量研究。比较典型的是Young等[7,8]和Deigutte[9]所进行的实验，他们在猫的听神经上进行测量,获得了数百根听神经纤维对于纯音、双音、宽带噪声及不同语音等各种简单或复杂声音刺激的响应数据。

大量生理实验结果说明，听觉系统对声音的基本表达方式是“音调拓扑的”(tonotopic)[8]，这种特性可由基底膜和听觉神经对频率的选择性充分体现。听觉功能在很大程度上由基底膜随声波的振动特性所决定，声波中的不同频率成分会引起基底膜不同部位的响应，因而具有滤波或频率分解作用。听觉神经纤维也按频率排列，每根神经对应一个最敏感的频率，称为“特征频率” (characteristic frequency，CF)[9]。通过测量神经纤维对不同频率的响应阈值可以发现，每根神经纤维所对应的曲线都是很陡的V字形曲线，曲线的最低点具有最小响应阈值，对应神经纤维的CF。而在CF两侧，随着频率的偏移，其响应阈值迅速提高[8,10]。

在听觉生理和心理学研究基础上，很多听觉外周计算模型相继出现，用以模拟声波作用下外周听觉系统不同部位的响应特性。这些模型可以模拟基底膜、内毛细胞及听神经对声波信号多方面的反应特性，能与实验数据很好地吻合[11～14]。随着对外周机制的深入研究，基于听觉计算模型的语音处理系统在语音识别、压缩编码等领域已得到广泛应用[15～20]。现有计算模型基本都采用滤波的概念，把基底膜看成一组并联的滤波器组，组中每个滤波器具有不同中心频率和带宽。比较有影响的是Fletcher[21]通过掩蔽实验提出的临界带 (critical bandwidth，BW)概念，把整个基底膜按长度均匀划分为25个区间，每个区间对应一个频带，称为“临界带”。

采用滤波器组模拟基底膜时，每个滤波器都具有一定带宽。以按临界带划分为例，在500 Hz以下时，每个临界带宽基本保持在100 Hz；而超过500 Hz以后，临界带的中心频率近似按20%的增长率逐渐增加。由此带来的问题是：每个频带中所包含的具体频谱成分应该如何由神经纤维来表达，或者说，每个频带与内毛细胞及听觉神经是什么样的对应关系，才能把声音中包含的所有频率成分准确地表达出来呢？这是目前还没有得到解决的问题。因此，现有计算模型还很难解释听觉系统所具有的高精度频率差阈分辨能力。很明显的例证是，按十二平均律排列的音乐音阶，两个相邻半音阶之比约为1.0595，频率越低则可鉴别的频差越小，在100 Hz时，相邻半音阶的频差约为6 Hz，在连续弹奏时，很多人都可以分辨出它们的差别，尤其是一些音乐家或专业调琴师，他 (她)们更是具有超乎常人的对音调变化灵敏的分辨能力。

我们研究的主要思路是，外周听觉系统的主要功能是实现声波的接收和信号形式的转换 (由声压转换为系列神经脉冲)，其目的是将声波信号所包含的频谱结构如实地传递至听觉中枢，最终由听觉中枢形成相应的听觉。听觉外周对信号的有效表达是形成听觉的先决条件，声音信号经外周听觉系统处理后损失的频率成分将无法在中枢形成相应的知觉，也就谈不上对这些频率成分的鉴别了 (但传递至中枢的信息也未必都能形成知觉，因为知觉形成过程还包含复杂的心理过程，如注意力的参与等)。基于以上研究思路，本文主要探讨听觉外周对声波的具体表达方式。

内耳生理结构及功能

听觉外周由外耳、中耳和内耳组成。其中，外耳和中耳是传声系统，负责把声源振动所引起的空气疏密波传递到内耳；内耳具有换能作用，可以将声波的机械能转变为听神经纤维上的神经冲动，也可以说是进行信号形式的转换。内耳的换能作用主要由耳蜗中的基底膜和内毛细胞，以及螺旋神经节中的听觉神经共同完成。人类的基底膜展开长度约35 mm，宽度由靠近卵圆窗的0.16 mm逐渐变宽，到最里端时达到0.52 mm。基底膜的刚度是不均匀的，靠近卵圆窗的地方 (最窄)刚性大，对应较高的共振频率,而最宽的地方刚性最小，对应较低的共振频率。生理研究已经表明，声波以行波方式沿基底膜传播，不同频率成分能够激起基底膜不同部位的振动,从而完成对声音信号的频率分解功能。当声音 (振动)经镫骨传到卵圆窗后，再由淋巴液传到基底膜，使基底膜靠近卵圆窗的部位与高频成分产生共振，离卵圆窗越远则共振频率越低。

耳蜗基底膜上分布着约3500个内毛细胞、15 000至20 000个外毛细胞[22]。其中，内毛细胞直接与螺旋神经节形成突触连接，构成耳蜗到脑干的传入神经通路，而外毛细胞则与螺旋神经节形成脑干至耳蜗的传出通路。每个内毛细胞连接一种神经纤维，唯一地代表一个特征频率。每个内毛细胞顶部排列着约100个静纤毛，静纤毛中间有离子通道，顶部有控制离子流量的闸门，相邻静纤毛上的离子闸门相互之间有细丝连接。当静纤毛由垂直状态向某个方向 (比如向右)倾斜时，会增加细丝之间的张力，使闸门逐渐打开，增强了向细胞内流入的K+电流，从而引起感受器电位的增加。当静纤毛顶部向右移动20 nm时，感受器电位发生饱和 (即闸门全部开放)，此时对应一个非常响亮的声音。静纤毛处于垂直或向左倾斜时，闸门之间的细丝处于松弛状态，使闸门一直处于关闭。因此，内毛细胞只有在基底膜向某个方向移动时才产生感受器电位，这就是很多研究中发现的内毛细胞的半波整流特性。K+流入内毛细胞导致其去极化，从而激活电压门控的钙离子通道。钙离子的流入促使神经递质的释放，进而激活内毛细胞突触后的螺旋神经节细胞，使其产生动作电位。

内毛细胞被夹在基底膜和一层网状板 (reticular lamina)之间，其顶部的静纤毛透过网状板进入内淋巴并终止于盖膜。当声波使基底膜振动时，网状板与盖膜之间形成侧向运动(亦称剪切运动，shearing motion)，使静纤毛向某一方向倾斜。如果静纤毛倾斜程度与基底膜振动幅度成正比，而听神经发放率又与内毛细胞感受器电位成正比，则可认为听神经发放率与基底膜振动幅度也成正比。这样，假如基底膜各段振动波形的组合代表进入耳蜗的声波信号，则声波信号最终由一组神经纤维来表达，即神经纤维的空间分布代表频率，神经脉冲发放率代表幅度。

基于离散余弦变换的耳蜗基底膜工作模型

离散余弦变换

离散余弦变换 (discrete cosine transform，DCT)类似于离散傅里叶变换，但只使用实数。离散余弦变换有多种不同形式，但最常用的是DCT-II，它被广泛应用于语音和图像信号的处理中，通常所说的离散余弦变换一般都是指这种形式。设输入信号的离散序列为x(n)，则其N点离散余弦变换及反变换可表示为：

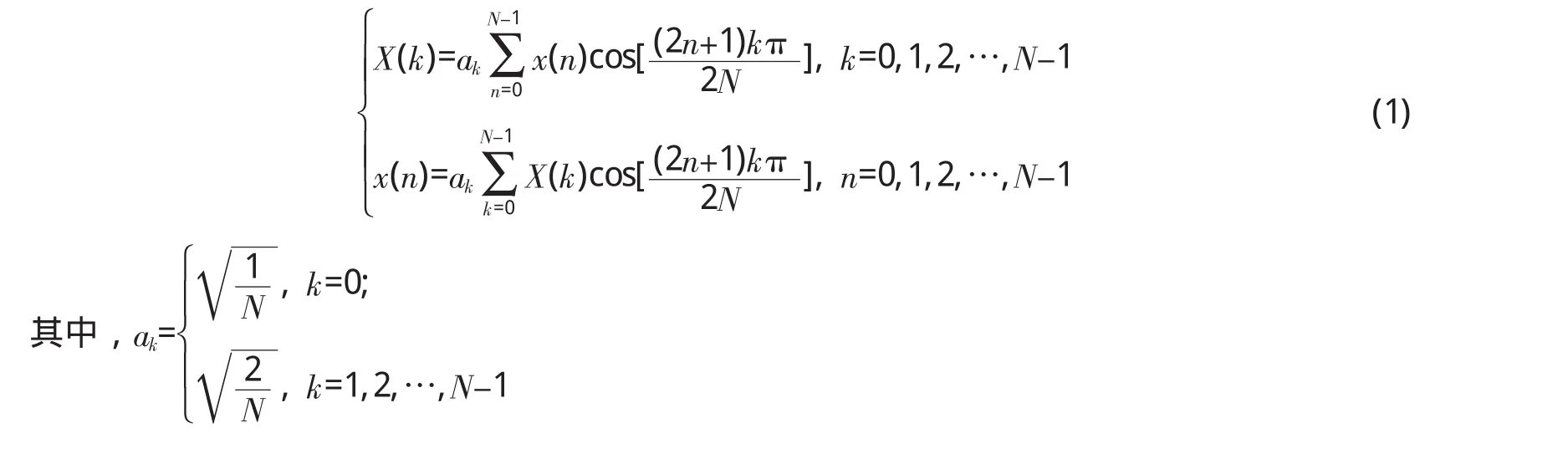
设原始音频信号包含M个频谱成分，表示为：

其中，xi(t)代表频率为fi的余弦信号。则x(t)对应的采样序列为：

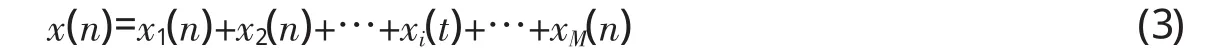
由于离散余弦变换是线性变换，x(n)的离散余弦变换可由每个频率成分的离散余弦变换求和得到，即：

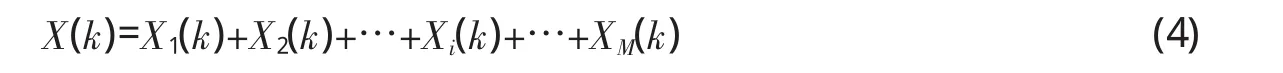
其中，当k取0,1,2,…,N－1时，得到N个离散余弦变换系数，每个系数对应一个频率，在此称为频率点。把每个频率点按1,2,…,j,…,N编号，则有j=k＋1。第j个频率点所代表的频率取决于采样点数N及采样频率Fs，具体关系为：Fj=(j－1)Fs/2N(j=1,2,…,N)。观察公式(1)和(4)不难发现，Xi(k)实际上就是初始相位为0、频率为Fk＋1的余弦函数与xi(n)对应采样点相乘再求和。根据余弦函数的特性，只有fi=Fk＋1且xi(n)初始相位等于0时，Xi(k)才具有最大值，此时，xi(t)的能量基本都集中在所对应的第k＋1个频率点上。否则的话，xi(t)的能量会分散在与fi最接近的几个频谱点上，而远离fi的其它频率点则迅速减小，直至接近或等于0。

假设某一音频信号x(t)由3个频率成分构成，即：

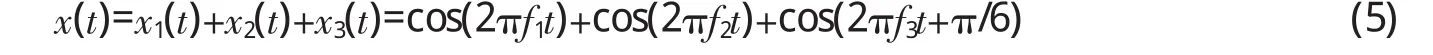
其中，f1=200 Hz，f2=203 Hz，f3=300 Hz。设采样频率Fs=44.1 kHz，采样点数N=4410，分别对x1(t)、x2(t)、x3(t)及x(t)进行离散余弦变换，图1是变换后的频域图。由于频率分辨率为5 Hz，图1横轴上每个频率点所代表的频率并不是连续的，只有频率为5的整倍数才能在横轴上找到对应点。

由于f1=200 Hz是5的整倍数，在横轴上对应第41个频率点，因此，其能量基本都集中在这一点上，而其它频率点则接近或等于0，见图1A。对于f2=203 Hz，由于不是5的整倍数，在频率轴上没有对应的频率点，因此，x2(t)的能量主要分散集中在第40～43几个频率点上，对应频率为195、200、205和210 Hz，如图1B所示。f3=300 Hz虽然在频率轴上对应第61个频率点，但由于x3(t)有π/6的初始相位，因此，它的能量也被分散在第60、61、62及附近的几个点上，见图1C。图1D是对x(t)进行离散余弦变换的结果，显然应有X(k)=X1(k)＋X2(k)＋X3(k)，即图1A、B、C对应频率点相加就可得到图1D。

通过分析离散余弦变换的本质特性，可以得到结论：对信号x(t)进行N点离散余弦变换，其实质就是用N个固定频率的余弦信号来代表它。具体来说，对于给定的x(t)，以采样频率Fs对其进行N点采样，经余弦变换后得到一个N维向量a=[a1,a2,…,aj,…,aN]，则x(t)可用N个余弦函数的和来表示，即：

基底膜工作模型

基底膜的频率分解作用

设将基底膜按频率均分为N段，每段对应一个内毛细胞，每个内毛细胞又连接一种神经纤维，则每段基底膜、内毛细胞及听神经纤维的组合形成一条信号通路，唯一地代表某个特征频率，如图2所示。当声波信号x(t)传递到基底膜时，被分解成N路输出，第j路输

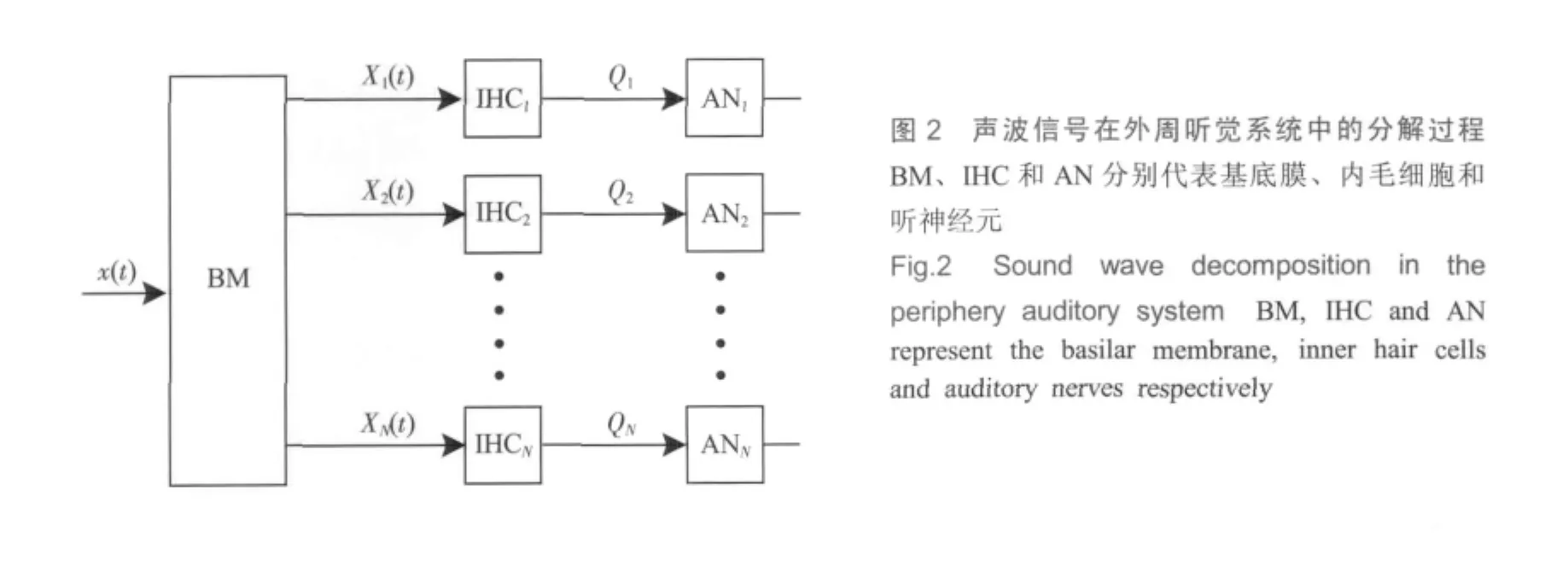
出用Xj(t)=Ajcos(2πFkt)表示，其中，Aj代表基底膜第j段的振动幅度，而Fj是该段的特征频率。假如N路输出波形与输入声波之间的关系满足式(8)，则声波信号可由基底膜各段振动波形表达。

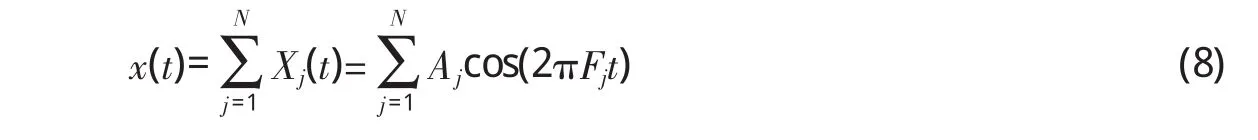
基底膜将声波按特征频率分解之后，特征频率本身即由它所对应的信号通路来表征。因此，只要内毛细胞和听觉神经元在能量转换过程中能够表达出基底膜的振动幅度，就可以表达出所有频率成分。很显然，只要使Qj=λAj、Rj=βQj，即可使Rj=λβAj，则每段基底膜振动幅度都可由神经脉冲发放率表示。其中，λ和β分别代表内毛细胞和听神经元的变换系数，是由内毛细胞的换能机制及听觉神经的编码机制所决定的，本文暂不具体探讨这两方面内容。由于内毛细胞、听觉神经都代表基底膜的振动幅度，因此，在后面讨论中统称为信号强度。

为确定式(8)中的Aj，我们把第j基底膜看成是初始相位为0、频率为其特征频率Fj的余弦函数，即bj(t)=αjcos(2πFjt)。当音频信号x(t)作用于该段基底膜时，如果定义其振动幅度正比于二者对应采样点相乘再求和，即)，则正好与音频信号的离散余弦变换具有相同形式。这样，当音频信号x(t)传入耳蜗时，第j路的输出就可以表示为aj=，其中，aj－1与 DCT-II定义相同。

当传入耳蜗的音频信号具有式(2)的形式时，xi(t)分量所引起的神经纤维输出为Qi=(i=1,2,…,M)，其中表示xi(t)作用于第j段基底膜时，在该信号通路的输出强度，可表示为式(9)的形式，

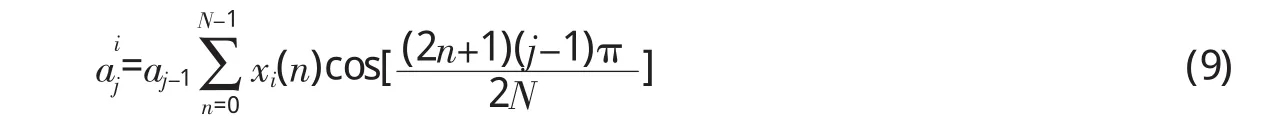
而x(t)所引起的总输出就是各个频率分量所引起的输出之和，即O=[a1,a2,…,aj,…,aN]，其中，是M个频率分量在第j根神经纤维中产生的输出。这样，通过基底膜的频率分解作用，就把x(t)转换成了一个N维输出向量，这个向量就代表了x(t)，或者说，x(t)是神经纤维输出向量O的函数，表示为x(t)=f(O)。

其物理意义是，任何音频都可以分解成N个固定频谱成分，而每个频谱成分的输出幅度与音频信号中频谱成分之间的关系满足余弦变换。如果N个固有频率用N根神经纤维来表示的话，则某根神经纤维的总输出就是音频信号中每一频率成分在该神经纤维中引起输出的叠加。

听觉神经纤维的频-时输出模式

声音信号是随时间变化的，不同时间包含不同信息。所以，听觉系统把进入耳蜗的音频信号沿时间轴分成很多微小的时间段，在此称为“工作时隙”，用ts来表示。在每一工作时隙内，听觉系统要对这一期间的语音信号进行处理，即：先通过外周把声波转换成神经冲动并通过神经纤维传递至中枢，然后由中枢进行识别和储存。生理学意义上的ts目前还没有完全确定，也未见这方面的相关研究资料，但很多现象显示其应该在0.1 s左右[23]。在本文研究中，ts的取值可由采样频率Fs和神经通道数量N共同确定，具体关系为：ts=N/Fs。采样频率根据wav格式音频文件的采样频率决定，取Fs=44 100 Hz，而N应取决于内毛细胞的数量 (3500左右)。为便于观察，实验中取N=4410，这样可以使频率分辨率为整数。

图3是内耳的工作模型，C1、C2、…、CN代表分布于基底膜不同部位的内毛细胞，对应的特征频率为F1、F2、…、FN。每个毛细胞单独连接一根神经纤维，则每根神经纤维唯一对应一个频谱成分，即频率成分是依靠神经纤维的空间拓扑关系来表达的。当声波信号x(t)按时间顺序传递到基底膜时，在第w工作时隙(w－1)ts～wts(w=1,2,3,…)内，第j根神经纤维将会产生一个输出ajw，而N根神经纤维在此工作时隙内形成的输出向量O(w)=[a1w,a2w,…,ajw,…,aNw]也就代表了该期间的音频信号，即x[(w－1)ts,wts]=f[O(w)]，而整个音频信号x(t)是由f[O(1)]、f[O(2)]、f[O(3)]等按时间顺序出现而形成的。这里，ajw是模拟量，其大小代表该频率分量的幅度，而符号则代表相位，听神经纤维在编码过程中应能表达出这两个要素。由于O(w)代表一段声音的频谱结构，因此可以称为“频谱模式 (spectrum pattern)”。这样，声波信号经内耳变换后就成为一系列按时间顺序排列的频谱模式，即“频-时模式(spectrotemporal pattern)”[9]。

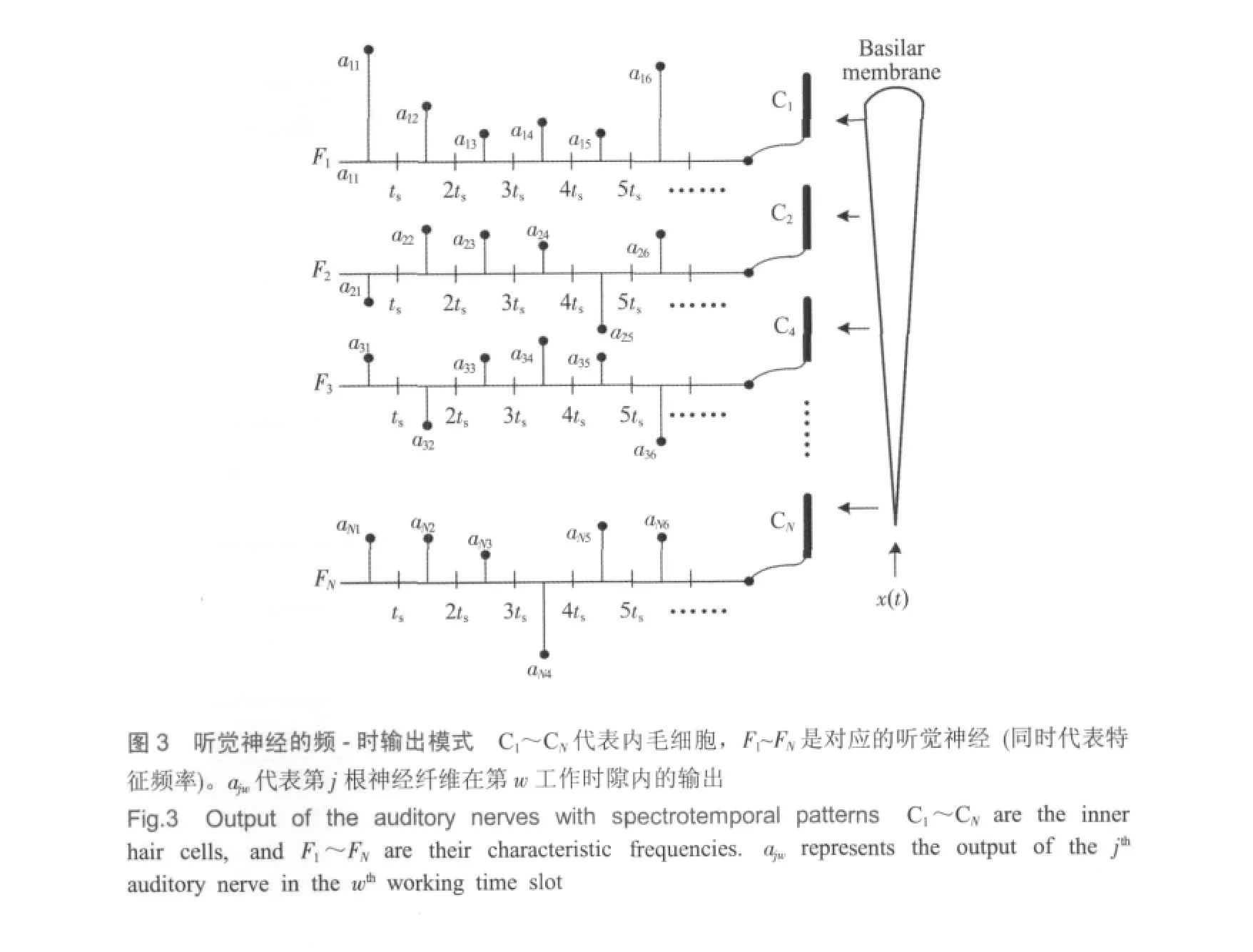
仿真实验结果

我们利用Matlab仿真软件对模型进行了仿真实验。以某男声“中”字的读音为例，其时长约为0.4 s，图4A是其完整时域波形。取采样频率Fs=44 100 Hz，神经纤维数N=4410，则每个工作时隙ts=0.1 s，整个时域波形被分割成四段，如图4B～E所示。在每个工作时隙内进行离散余弦变换，结果见图5。实验结果表明，语音信号频谱能量主要集中在j=800以前，即对应频带宽度为20～4000 Hz；当j＞800时，离散余弦变换系数a(j)将随j的增加快速衰减至趋近于0。为便于观察，图5只给出了j≤200的情况。

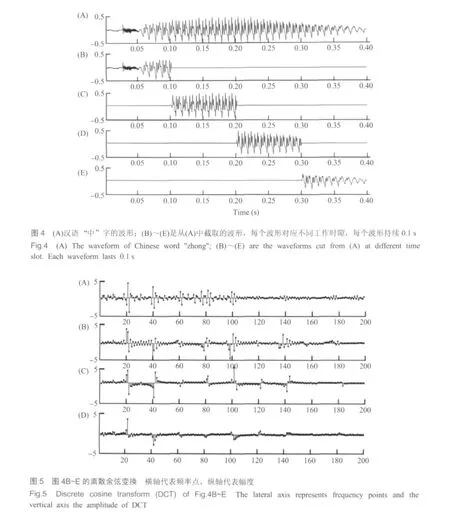
图5A～D中，横轴上的每个点对应一根神经纤维，神经纤维的特征频率与j的关系满足余弦变换，即满足公式(1)。 因此，图5A～D的横轴代表200根神经纤维，其特征频率由低到高依次为0、5、10、15、…、995 Hz；而纵轴是离散余弦变换系数a(j)，代表每根神经纤维在四个工作时隙内的输出幅度。根据离散余弦变换的性质，如果音频信号中的某一频率成分与某段基底膜特征频率相同，则对这段基底膜的作用最大，且对其它基底膜的作用迅速减小。而如果某一频率成分没有对应的特征频率，则这一频率成分将分散作用在具有相近特征频率数段的基底膜上，具体的幅度分布还与这一频率成分的相位有关。图5A中幅度突出的区域，如j=20、40、60、80等点的附近，是频谱能量较为集中的频谱区域，也可看作是该音频信号共振峰分布的区域。由于离散余弦变换是用N个固定频率来表达时域信号中包涵的所有频率成分，因此，从变换结果上一般不能直接看出原音频信号中所含有的具体频率成分。例如，图5A中，j=17～23这7个点幅度比较突出，这些点代表的频率依次是80、85、90、…、110。但这并不说明原来的音频信号中肯定包含这几个频率成分，而只能说明它含有100 Hz左右的频率，而具体包含几个及具体的频率和相位都是无法完全确定的。

从数学变换的角度来看，每一段声波信号唯一对应一个频谱模式。理想情况下，如果听觉外周能将这个模式完整地投射至中枢，则意味着听觉神经对这段声波的表达是精确的。很显然，只有基底膜、内毛细胞和听神经元在信号变换过程中总能使输入和输出之间保持理想的线性关系。变换过程的非线性会使原有信号频谱模式发生改变，即某些频率成分在信号中的比重与原信号相比增加或降低了，甚至产生原信号中所没有的新成分[25]，由此造成信号失真。因此，利用余弦变换对声波信号进行变换以后，可以根据听觉外周产生非线性的原因、机理及对频谱模式的影响，对原有的频谱模式进行修正，就可对真实的外周生理现象进行模拟或描述，还可以分析各种原因产生的波形失真对听觉的影响。为说明这一点，我们以小信号频谱成分丢失的情况为例进行讨论。当声波信号中所包含的某个频率成分幅度太小，达不到听神经的响应阈值时，则该段基底膜所对应的神经纤维无输出 (或者只保持自然发放率)，就可能造成该频率成分的损失；又如，随着人的衰老，内耳机能也会逐渐减退，基底膜、内毛细胞及螺旋神经节的老化或损伤都有可能使响应阈值提高，微弱的频率成分不能激起它们的响应，从而造成小信号频谱成分的损失。

设输入声波信号为x(n)，对应的离散余弦变换系数为：在处理声波的过程中，如果内耳使某些频率成分发生幅度上的改变，即产生一个新频谱模式：

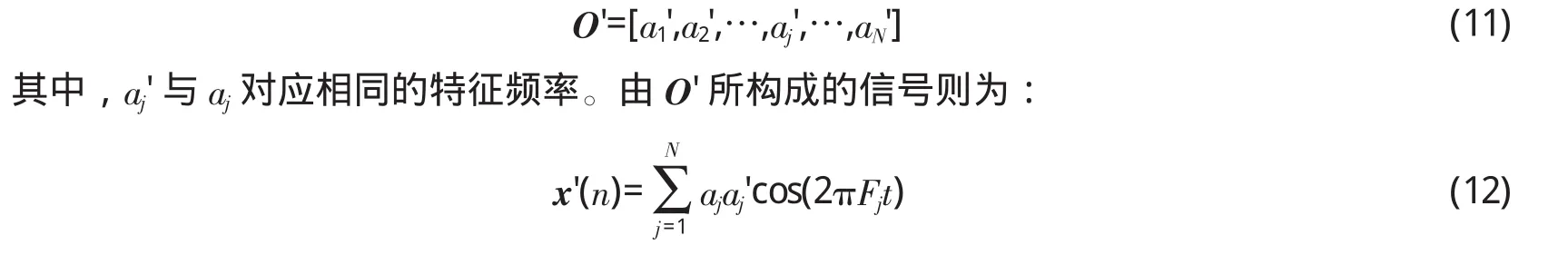
显然，只有当O=O'时才有x(n)=x'(n)，否则二者存在差别，即产生了信号失真。针对某一声波信号，实验中设定一个阈值θ，当θ时令aj'=0，否则aj'=aj。然后根据式(12)计算x'(n)，并按下式计算其与原信号x(n)的相似度ρ：

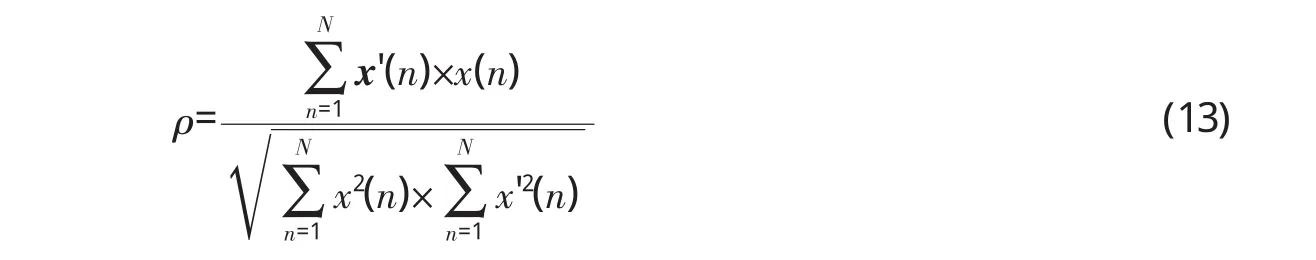
通过改变θ，即可获得一条ρ随θ变化的曲线，如图6所示。横坐标θ¯是相对于最大幅度的归一化值，即θ¯=θ/max(O)。当θ¯=0、ρ=1时，代表没有频率成分损失，即两个信号波形一致；θ¯取值越大则损失频率成分越多，x'(n)与x(n)的相似度也就越低。图中七条曲线分别代表“中华人民共和国”这七个汉字的男声读音，每个字对应的曲线由汉语拼音标出。曲线下降越快，说明这段语音中小信号频率成分所占比重越大。

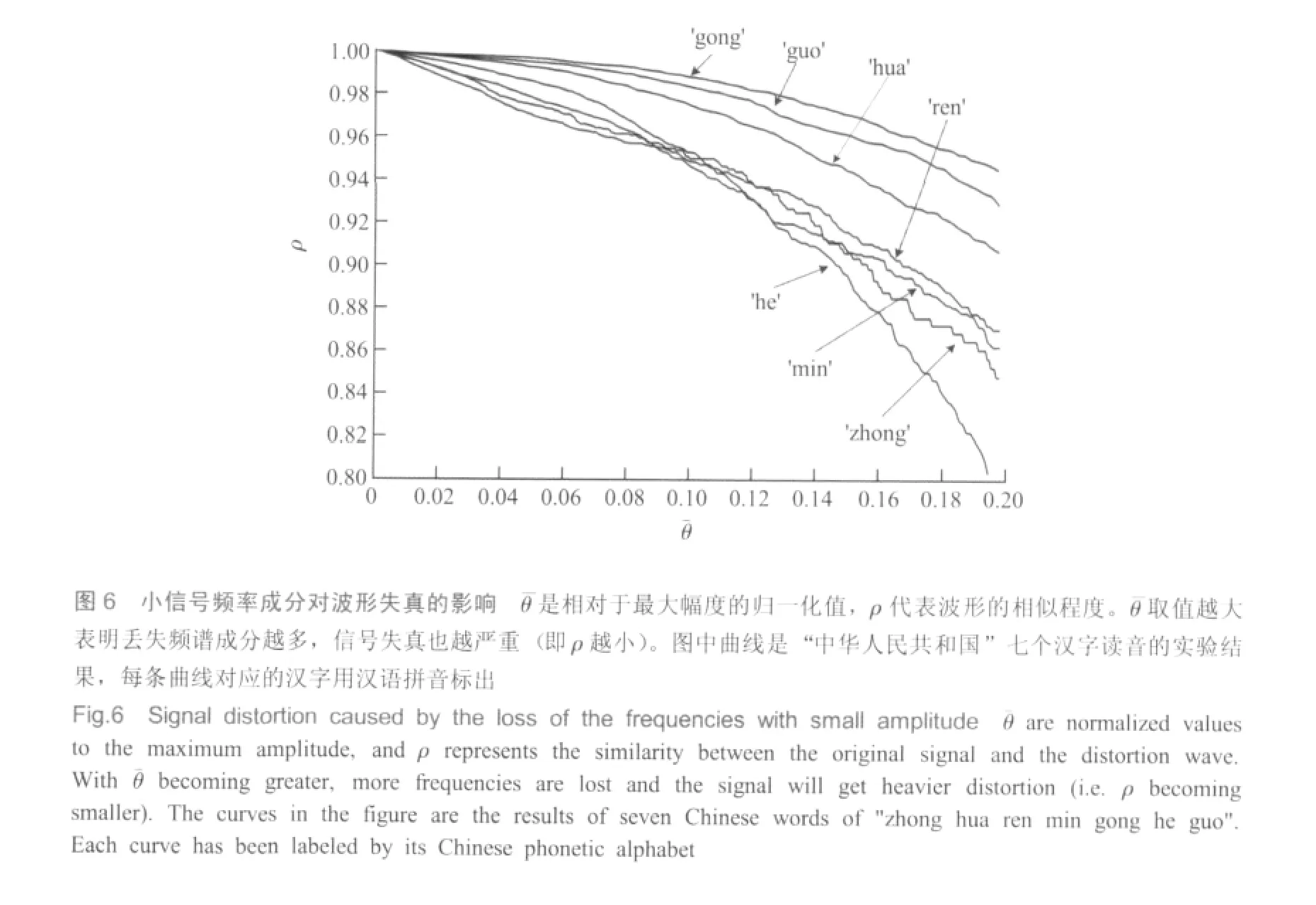
实验结果表明以下两点：1)听觉系统对小信号频率成分的损失非常敏感。对于所有读音，只有当小信号损失使ρ不低于0.995时 (只是近似，而且每个字也有区别)，才听不出音质或音色有明显变化，此时对应的θ¯＜0.02。因此，为确保音频质量，在神经编码过程中对小信号成分应具有更精确的表达，否则将引起较大噪声或失真；2)同时，听觉系统对信号失真的容忍度又具有很好的鲁棒性。当θ¯从0开始逐渐增加时，虽然与原声音相比可以明显感觉出音质变化，但在很大范围内都可以清晰地辨别出每个字的发音。直到θ¯=0.2时，虽然还可以分辨出每个字，但都有不同程度的含混感。由此可见，小信号频率成分对语音信号的构成起着至关重要的作用。在强噪声中，我们往往能听见某人在说话，但就是听不清说话内容，可能就是因为小信号频率成分被噪声所覆盖的缘故。

结 论

现有研究只明确了耳蜗基底膜及毛细胞具有频率分解作用，可以把进入耳蜗的时域信号转换成按空间分布的、具有不同特征频率的神经纤维输出，但二者的具体关系尚不十分明确，有关这方面的文献并不多见，特别是国内同行在该领域的研究也不十分广泛。本文利用离散余弦变换的频率分解作用，描述语音信号与听觉神经纤维输出之间的对应关系，即进入耳蜗的声波信号可由一组代表不同频率的神经纤维输出来代表，神经纤维输出强度由音频信号的离散余弦变换确定，这一特征与实际外周听觉系统所具有的音调拓扑结构相吻合。从信号表达及变换的角度来看，只有听觉神经输出与声波信号之间保持严格的线性关系，才能保证我们所听到的声音是无失真的。但从听觉系统的角度又允许有一定的失真，即只要感觉不到失真就可以认为是无失真的。生理研究也确实发现外周听觉系统还具有非线性特性。为此，我们首先假定听觉外周是个线性系统，然后利用线性变换 (即离散余弦变换)得到其输入和输出之间的关系，再根据非线性产生的原因及对频谱模式的影响，对离散余弦变换结果进行修正，就可以模拟和分析实际外周听觉系统的工作特性。这也是工程上广泛采用的处理系统非线性问题的主要方法。文中以小信号频率损失对波形失真的影响为例进行了初步探讨。

1. Bekesy GV.On the elasticity of the cochlear partition.J Acoust Soc Am,1948,20(3)：227～241

2. Zwislocki JJ. Five decades of research on cochlear mechanics.J Acoust Soc Am,1980,67(5)：1679～1685

3. Rhode WS.Observations of the vibration of the basilar membrane in squirrel monkeys using the MÖssbauer technique.J Acoust Soc Am,1971,49(4)：1218～1231

4.Rhode WS,Robles L.Evidence from MÖssbauer experiments from nonlinear vibrations in the cochlea.J Acoust Soc Am,1974,55(3)：586～596

5.Rhode WS,Recio A.Study of mechanical motions in the basal region of the chinchilla cochlea.J Acoust Soc Am,2000,107(6)：3317～3332

6. Recio A,Rhode WS.Basilar membrane responses to broadband stimuli.J Acoust Soc Am,2000,108(5 Pt 1)：2281～2298

7. Young ED,Sachs MB.Representation of steady-state vowels in the temporal aspects of the discharge patterns of populations of auditory nerve fibers.J Acoust Soc Am,1979,66(5)：1381～1403

8. Young ED.Neural representation of spectral and temporal information in speech.Phil Trans R Soc B,2008,363：923～945

9. Delgutte B.Auditory neural processing of speech.In：Hardcastle WJ, Laver J. The handbook of phonetic sciences.Oxford：Blackwell,1997：507～538

10.Taberner AM,Liberman MC.Response properties of single auditory nerve fibers in the mouse.J Neurophysiol,2005,93(1)：557～569

11.王仁华,夏德瑜,付前杰.外周听觉系统的计算模型,生物物理学报,1991,7(4)：436～441 Wang RX,Xia DY,Fu QJ.A computational model for the peripheral auditory system.Acta Biophys Sin,1991,7(4)：436～441

12.陈卫兵,周凌宏,肖中举.耳蜗基底膜振动模型的建立与应用.中国医学物理学杂志,2007,24(3)：221～223 Chen WB, Zhou XL, Xiao ZJ. The foundation and application of basilar membrane's vibrant model.Chin J Med Phys,2007,24(3)：221～223

13.Lyon RF.A computational model of filtering,detecting and compression in the cochlea. Proc ICASSP,1982,82(7)：1282～1285

14.Meddis R.Simulation of mechanical to neural transduction in the auditory receptor.J Acoust Soc Am,1986,79(3)：702～711

15.Robinson DJM.Perceptual model for assessment of coded audio.Ph D Issertation,2002,Colchester：University of Essex

16. Perceptual coding of digital audio, ted painter and Andreas Spanias.http：//www.mp3-tech.org/programmer/docs/audiopaper1.pdf[2012-6-12]

17.Dau T,Puschel D.A quantitative model of the"effective"signal processing in the auditory system.I.Model structure.J Acoust Soc Am,1996,99(6)：3615～3622

18.Moore BCJ.Coding of sounds in the auditory system and its relevance to signal processing and coding in cochlear implants.Otol Neurotol,2003,24(2)：243～254

19.卢绪刚,陈道文.基于时间机理与部位机理整合的鲁棒性语音信号表达.生物物理学报,1999,15(3)：524～529 Lu XG,Chen DW.Robust speech signal representation based on integrating spatial and temporal mechanisms.Acta Biophys Sin,1999,15(3)：524～529

20.王磊,彭圆,林正青,蒋行海,牟林,张凤珍.听觉外周计算模型在水中目标分类识别中的应用.电子学报,2012,40(1)：199～203 Wang L,Peng Y,Lin ZQ,Jiang XH,Mu L,Zhang FZ.The application of computational auditory peripheral model in underwater target classification.Acta Electron Sin,2012,40(1)：199～203

21.Fletcher H.Auditory patterns.Rev Mod Phys,1940,12：47～65

22.Bear MF,Connors BW,Paradiso MA.Neuroscience：exploring the brain. Third edition. Baltimore：Lippincott Williams&Wilkins,2007：344～361

23.Baars BJ,Gage NM.Cognition,brain and consciousness.Second edition.Oxford：Elsevier Ltd,2010：5～8

24.Meddis R.Auditory-nerve first-spike latency and auditory absolute threshold：A computer model.J Acoust Soc Am,2006,119(1)：406～417

25.Robles L,Ruggero MA,Rich NC.Two-tone distortion in the basilar membrane of the cochlea.Nature,1991,349：413～414