风电机变桨驱动减速器摆线轮的有限元模态分析
2013-09-20李纪顺蒋英兰何卫东
李纪顺,蒋英兰,何卫东,
(1.大连交通大学 机械工程学院,辽宁 大连 116028;2.集美大学 轮机工程学院,福建 厦门 361021)*
0 引言
针摆行星传动是一种具有广泛应用前景的新型传动.针摆行星传动具有传动比范围大、硬齿面(轴承钢)多齿啮合、体积小、运动平稳、使用寿命长、噪声低、承载能力大以及传动效率高等显著优点[1].目前在诸多机械行业中已经被广泛应用,并且在整个减速器业内也占有较大比例的市场份额.面向高速、重载的发展需要,加强了对轻量化、运转平稳的要求,怎样减少疲劳破坏、减轻振动噪声已经成为以后机械研发的重点内容,如果机器内部结构设计不合理,导致系统动态性能不理想,在运行过程中就可能产生减少机器寿命的不良振动和噪声.经查文献,对于两级针摆行星减速器传动部件的模态分析尚少,本文以传动比i=165的两级针摆行星减速器为例,用ANSYS分析软件对减速器内部摆线轮进行模态分析,得到摆线轮的固有频率及振动形态,为避免共振及有害振型的出现和深入的动力学研究奠定了基础.
1 建立摆线轮三维实体模型
ANSYS有限元分析软件对于复杂实体模型的绘制能力不是很强大,不能够方便快捷的生成比较复杂的摆线轮齿廓曲线,因此本文应用Pro/E来建立摆线轮的三维实体模型.该软件只要输入曲线方程,即可直接生成摆线轮齿廓曲线[2].
1.1 建立摆线轮齿廓曲线直角坐标方程
摆线针轮行星传动中摆线轮的齿廓曲线大多采用短幅外摆线的内侧等距曲线,其成型原理是半径为rg的滚圆(发生圆)在半径为rbc的基圆(固定不动)上纯滚动时,滚圆圆周上一点的轨迹为外摆线,而滚圆内部一点的轨迹称为短幅外摆线(属变幅外摆线)[3].
齿廓摆线在直角坐标系下的方程如下式[4]:

式中,rrp为针齿半径;rp为针齿中心圆半径;Zc为摆线轮齿数;K为短幅系数K=A·Zp/(rp+Δrp);i为相对传动比i=Zp/Zc;A为偏心距;Δrrp为等距修形量;rp为移距修形量;其中,α=360·Zc·t,t=0 ~ 1;Zp=Zc+1;Sr=1+K2-2Kcosα;drp=rp+Δrp-(rp+Δrp-+ Δr(A/(rpp))·(rp+ Δrp-Zp·(rp+ Δrp)
1.2 建立摆线轮参数化模型
本文所研究的是风电用变桨距驱动减速器的摆线轮,第一级摆线轮所需参数如下:传动比为11,针齿数为24,摆线轮有效宽度为12 mm,偏心距为5.5 mm,针齿中心圆直径为176 mm,针齿套直径为13 mm,转臂轴承外滚道直径为68.225 mm,柱销数为8,柱销中心圆直径为112 mm,柱销孔直径为31.5 mm.第二级摆线轮所需参数如下:传动比为15,针齿数为32,摆线轮有效宽度为19 mm,偏心距为7 mm,针齿中心圆直径为330 mm,针齿套直径为22 mm,转臂轴承外滚道直径为151.58 mm,柱销数为12,柱销中心圆直径为224 mm,柱销孔直径为48.15 mm.
首先在Pro/E中选择“工具”,以下拉菜单中选择“关系”建立所需的关系及局部参数.建立曲线,在曲线选项中选择“从方程”,之后选取笛卡尔坐标即直角坐标系,在文本里输入摆线方程即可创建模型所需要的曲线,对其进行旋转等编辑得到本文摆线轮的齿廓曲线,然后通过拉伸等操作来创建摆线轮的实体模型.摆线轮尺寸参数若有改动可以根据需要的数据修改关系中的表达式及局部参数来重新生成新的摆线轮模型.摆线轮三维模型见图1所示.
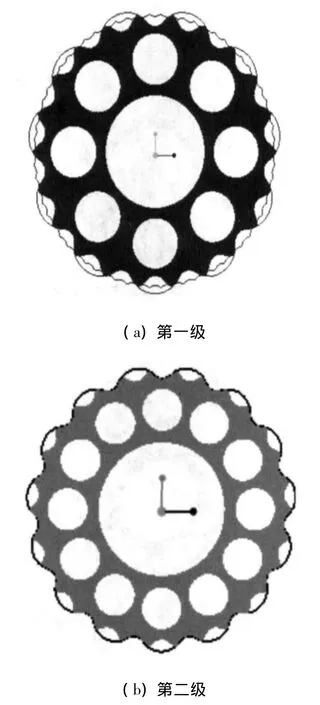
图1 摆线轮实体模型
2 摆线轮有限元模态分析
2.1 摆线轮无约束自由模态分析
将上述建立好的两个模型保存成IGES格式后分别转入到ANSYS中,并对其进行无约束状态下的模态分析.从理论上讲,自由边界条件下所计算得到的模态参数可以通过数学建模的方法计算得到任意边界约束条件下的特性;反之,在指定边界条件下取得的计算结果则不能转化为其他边界约束条件下的动特性[5].所以对摆线轮进行在自由边界支撑条件下的模态分析同样具有重要意义.
(1)单元类型设置成Solid Tet 10node 92(solid92).Solid92是三维十节点四面体单元,在保证精度的同时允许使用不规则的形状,它有相同的位移开关,每个节点有3个自由度:沿节点坐标x、y、z方向的平动,具有塑性、膨胀、蠕变、应力强化、大变形和大应变能力[6].由于摆线轮齿廓曲线的不规则性,选用Solid92三维十节点四面体单元可以较好地来拟合摆线轮齿廓曲线.
(2)定义材料属性:材料的弹性模量E=2.06×1011Pa,泊松比μ=0.3,密度ρ=7 850 kg/m3.

图2 有限元模型图
(3)划分网格:网格质量是指网格几何形状的合理性,是否能合理的拟合模型边界曲面,质量好坏将影响计算精度,不好的网格会中止计算过程.网格划分的质量和密度对有限元分析的计算结果有较大影响,网格的质量直接影响最后的分析结果[7].由于摆线轮齿廓曲线的复杂性,本文针对齿顶处网格做了细化处理,最终第一级摆线轮模型划分为41 029个单元,共计73 612个节点;第二级摆线轮模型划分为54 532个单元,共计91 662个节点.如图2.
(4)指定分析类型:模态分析.
(5)扩展模态阶数:零部件的振动形态可表示为各阶固有频率对应振型的线形组合,其中低阶振型对零部件的振动影响较大,相比之下也具有更重要的实际意义,所以在进行有限元模态分析时一般输出5~10阶模态,本文中计算出前10阶摆线轮固有频率并分析其振动形态.
(6)模态计算及结果分析:利用ANSYS分析软件强大的计算功能,可解出前10阶固有频率.计算结束后,在ANSYS的通用后处理器General Postprocessor查看计算结果,列表1列出第一级摆线轮各阶固有频率值,选择振型显著的第三阶、第四阶振型图,如图3所示.

图3 一级摆线轮振型图

表1 无约束状态下第一级摆线轮各阶固有频率及振型
列表2列出第二级摆线轮各阶固有频率值,选择振型显著的第3阶、第5阶振型图,如图4所示.
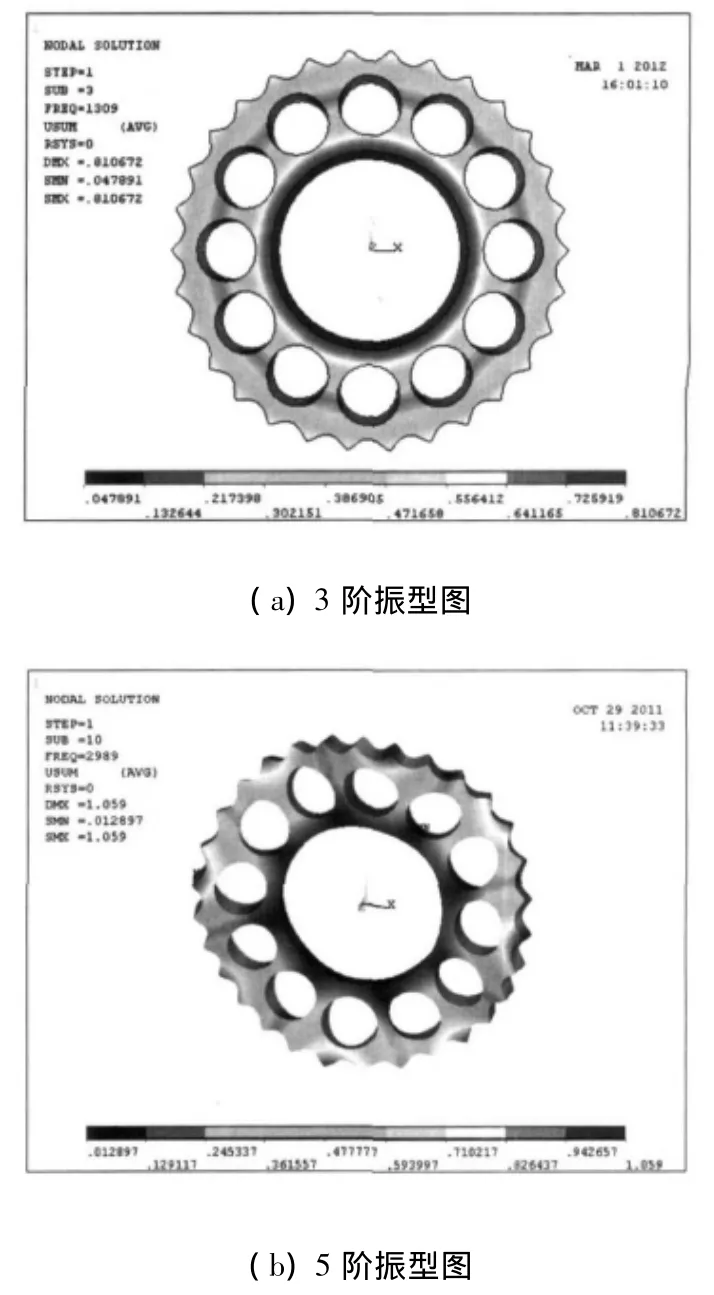
图4 二级摆线轮振型图
2.2 摆线轮实际边界约束下的模态分析
摆线轮自由模态是其固有特性,而分析它在与实际边界条件相近的约束下的模态,更能准确的反映出摆线轮在传动过程中的动态特性.本文在前面划分网格模型的基础上对摆线轮添加约束,摆线轮与转臂轴承紧密接触,在其接触位置上添加径向约束(即UX与UY两个方向),因为两者接触面积达不到整个圆柱面,所以只添加略小于1/2圆柱面的约束,约束添加完成后进行求解,添加约束后的模型如图5,计算结果由表3、表4分别列出.
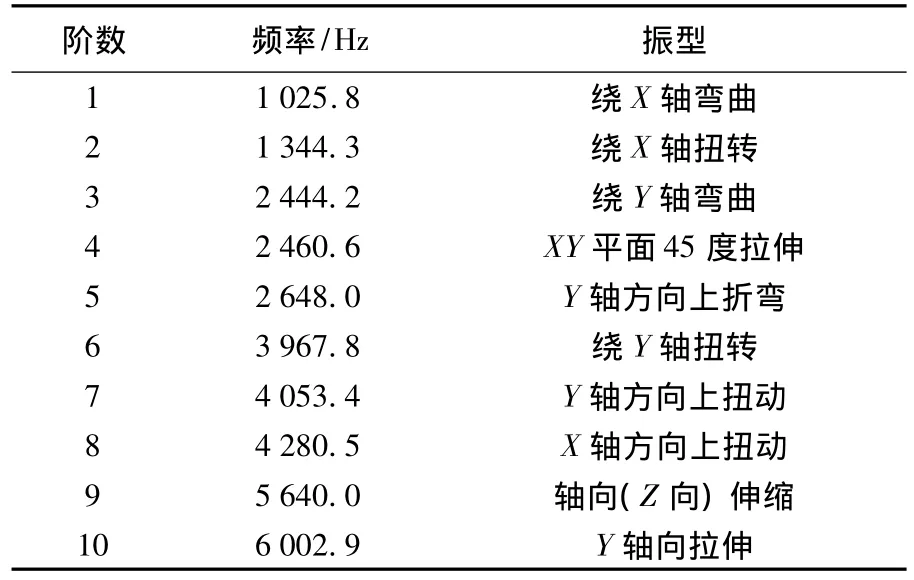
表3 实际边界约束下第一级摆线轮各阶固有频率及振型
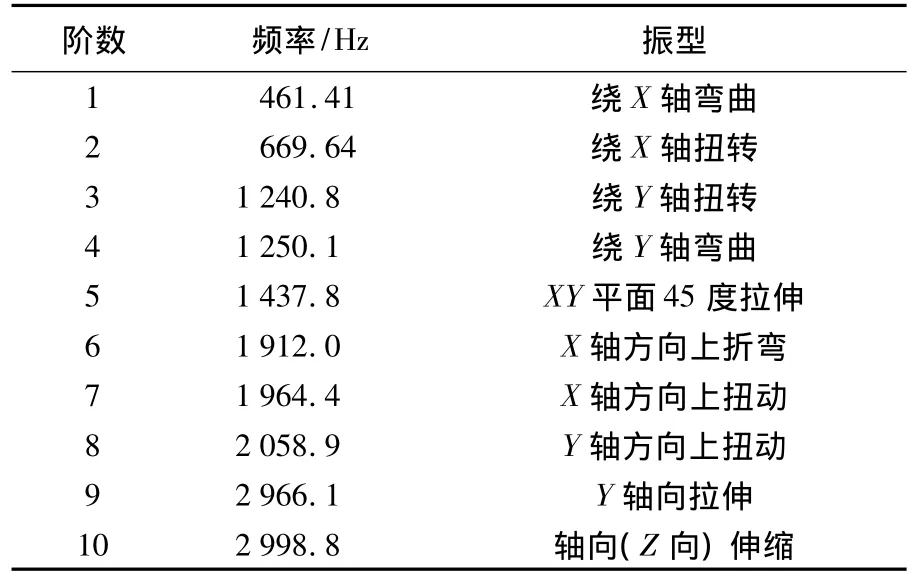
表4 实际边界约束下第二级摆线轮各阶固有频率及振型
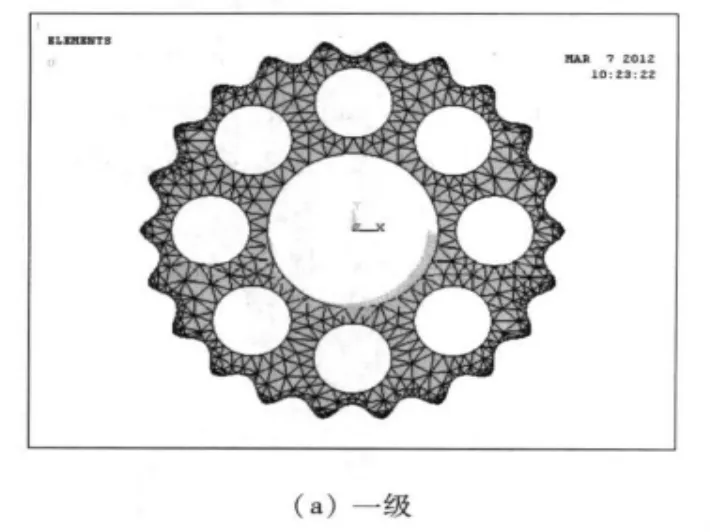
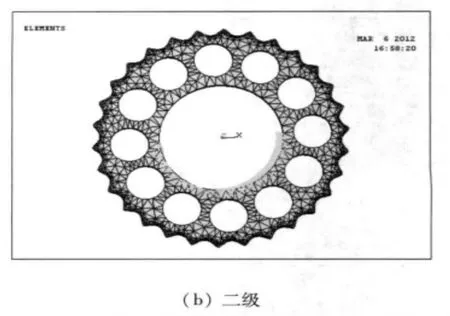
图5 摆线轮添加约束图
通过对比可以看出,摆线轮实际边界支撑下的固有频率值略小,分别列出振型显著的第3阶和第5阶振型图,如图6、7所示.

图6 一级摆线轮实际边界约束振型图


图7 二级摆线轮实际边界约束振型图
3 结论
通过将Pro/E中创建的摆线轮模型直接导入到ANSYS分析软件中,分别对其无约束和实际边界约束情况下的模态进行分析并说明分析方法,得出如下结论:
(1)本文在Pro/E中精确地创建立了摆线轮参数化模型,在以后深入的研究中可以通过修改齿形参数来快速生成新的摆线轮模型,这样大大提高了设计准确性及其效率;
(2)观察摆线轮的振型图可知摆线轮最大位移发生在齿顶及轴承孔的边缘,为以后优化设计提供依据;
(3)通过ANSYS软件求解,分别获得了两片摆线轮在无约束和实际边界约束下前10阶的频率值,并且分析得出其相应的振动形态,为摆线针轮传动动态性能方面的设计与实验提供了参考数据,同时也为进一步的动态分析及优化奠定了基础.
[1]何卫东,李欣,李力行,等.双曲柄环板式针摆行星传动降低振动与噪声的优化设计与试验[J].机械工程学报,2010,12,46(23):54-55.
[2]詹友刚.Pro/Engineer中文野火版4.0范例教程[M].北京:清华大学出版社,2010:108-125.
[3]机械设计手册编委会.机械设计手册[M].北京:机械工业出版社,2004:84-85.
[4]现代机械传动手册编委会.现代机械传动手册[M].北京:机械工业出版社,2002:84-86.
[5]项林.汽车前轴静动态有限元分析[D].广西:广西大学,2008.
[6]博弈工作室.ANSYS9.0经典产品基础教程与实例详解[M].北京:中国水利水电出版社,2006:59-67.
[7]肖君君.何卫东.RV减速器摆线轮的有限元模态分析[J].机械工程师,2009(9):46-47.
