分数阶神经网络控制器自顶向下优化方法

李文，亓芳，聂冰

(1.大连交通大学 软件学院，辽宁 大连 116028;2.大连交通大学 电气信息学院，辽宁 大连 116028)*

0 引言

目前，神经网络理论与应用研究已经广泛应用于专家系统、工业控制以及模式识别等领域.采用误差逆传播算法训练的多层前馈网络BP网络是应用最广泛的神经网络模型之一.然而，BP神经网络的结构通常根据经验选取，结构单一，无法根据系统的实际情况而实时调整网络结构，缺乏科学性.

本文设计了基于BP神经网络的分数阶PIλ控制器，并提出自顶向下优化BP神经网络的方法，系统结构如图1所示.实验结果表明通过这种优化神经网络结构的方法，删除冗余节点，精简网络结构，增强了BP神经网络的适应能力［4］.

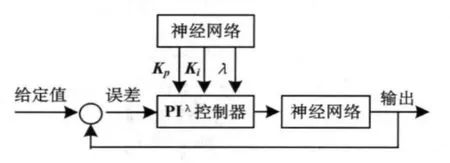
图1 基于神经网络的分数阶PIλ控制器框图

1 分数阶PIλ控制器的设计［1］

分数阶PIλ控制器是由整数阶控制系统扩展而来，其分数阶控制器的传递函数表达式为:

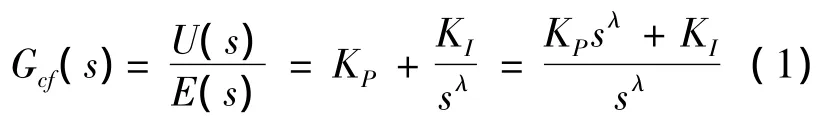
式中，KP、KI分别为控制器的比例系数和积分系数;λ＞0是分数阶控制器的积分阶次，可表示为任意实数.

分数阶控制器具有无限阶次，需要对分数阶微积分算子sλ进行离散化［7］.本文采用Tustin生成函数和连分式方法(CFE)结合对分数阶控制器进行离散化，三阶展开得到离散表达式为:

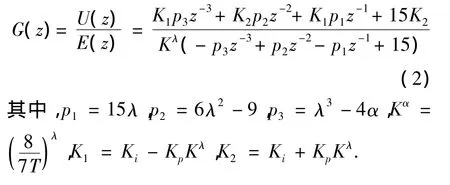
则U(z)时间域的离散表达式为:

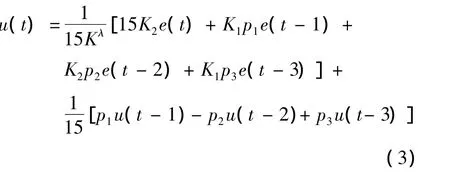
2 分数阶PIλ控制器自顶向下优化神经网络的方法

本文采用BP神经网络对PIλ控制器中的KP、KI和λ三个参数进行调节，利用自顶向下的方法优化网络的结构，提高神经网络的性能.

2.1 经典BP神经网络学习算法［3］

BP神经网络是一种按照误差算法训练的多层前馈网络，广泛的应用于各种工业控制领域.在BP神经网络中，输入层各神经元接收输入信息，传递给隐层各神经元;隐层是内部信息处理层，负责信息变换;最后隐层传递到输出层各神经元的信息，经进一步处理后，完成一次学习的正向传播处理过程，由输出层向外界输出信息处理结果.当实际输出与期望输出不符时，进入误差的反向传播阶段.误差通过输出层，按误差梯度下降的方式修正各层权值，向隐层、输入层逐层反传.周而复始的信息正向传播和误差反向传播过程，是各层权值不断调整的过程，也是神经网络学习训练的过程.该循环过程一直进行，直到网络输出的误差减少到可以接受的程度，或者达到预先设定的学习次数为止.在文献［3］和［6］中对经典BP算法作了详细的介绍.

2.2 自顶向下优化BP神经网络的条件

在分数阶PIλ控制器中，输入层和输出层节点数是由系统本身的特点决定的.本系统选择输入层节点四个:X=(e，e-1，ce，ce-1);输出层节点三个:Y=(KP，KI，λ).而隐层层数和维数的选择决定了网络的规模.如果选择的神经网络规模过大，则神经网络逼近能力过剩;选择的神经网络规模过小，则神经网络的逼近能力不足，在学习的过程中不可能收敛.Robert Hecht Nielson等人指出:只有一个隐层的神经网络，只要隐节点足够多，就可以以任意精度逼近一个非线性函数［4］.因此，隐层节点数的确定是神经网络设计的重要内容，构造一个可变结构的网络，根据系统的实际情况自学习的调整结构，得到隐层节点数适合的神经网络.

本系统根据节点之间的相关性采用自顶向下优化神经网络的方法确定隐层节点数.自顶向下设计方法的核心思想是先构造一个足够大的网络，通过在训练中删除或合并某些节点或权值达到精简结构的目的［5］.首先计算隐节点输出之间的相关性，然后将相关性较大的冗余隐节点合并，最终确定合适的神经网络隐节点个数.

在训练神经网络的过程中，计算两个隐节之间的相关性为:

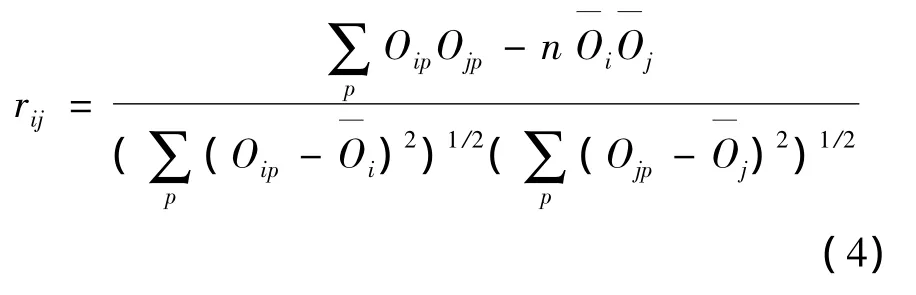
式中，Oip和Ojp是i和j两个隐节点对第P个样本的输出，输出均值分别为

对于任意的隐节点a的输出标准差为:s2a=

当两个节点相关性|rij|越接近1，说明这两个节点的线性相关性越高，存在冗余的节点需要合并;当某个节点的输出标准差较小时，则该隐节点对网络训练作用较小，可以删减.

根据上述计算公式，自顶向下优化神经网络的基本原则为:

(1)如果隐层两个节点相关性|rij|≥α1，且输出标准差s2i＞ α2，s2j＞ α2，则隐节点i和j可以合并.其中α1和α2为规定的下限值，一般α1取0.8 ～ 0.9，α2取0.001 ～ 0.01;

(2)若某节点的输出标准差sa≤α2，则说明节点a的作用较小，可以将其删除.

2.3 自顶向下优化BP神经网络的方法

由上述合并条件，结合经典BP神经网络学习算法，得到自顶向下优化神经网络算法的步骤如下:

(1)网络初始化:确定系统输入层、输出层和隐层节点数;随机初始权值;学习系数;合成时刻误差ε1;目标误差ε2;节点相关性阀值α1;输出标准差阀值α2;初始学习步数k=1;

(2)采用BP算法进行学习，同时计算所有隐节点输出序列;

(3)判断误差是否满足合成、终止学习条件:如果当前训练误差值E＞ε1，K=K+1转到步骤(2);如果 ε1≥E≥ ε2，转到步骤(4);E ＜ ε2，则终止学习;

(4)计算各隐节点输出序列的标准差和相关性;

(5)检查并合并隐节点:如果隐节点i和隐节点j相关系数满足|rij|≥ α1，且s2i＞ α2，s2j＞ α2，则对隐节点(i，j)进行合并;如果某个隐节点输出标准差满足s2i＜ α2，则删除该节点，K=K+1，转到步骤(2).

3 应用实例

以二阶系统 Y(t)= Y_set(1-e(-t/ξωn)*sinωdt)为例，取合成时训练误差 ε1=0.03，目标误差ε2=3*10-4，节点相关性阀值α1=0.9，输出标准差阀值α2=0.01，初始权值产生范围［-1，1］，初始网络结构为4-10-3网络.经过自顶向下方法优化后，本神经网络结构优化为4-2-3网络.停止学习后，输出序列相关性高于阀值两个隐节点合并，其部分合并隐节点的输出序列如图2所示.图3显示了该系统的输出响应曲线.图4所示为训练样本的学习曲线，在每次合并隐节点后，神经网络的训练误差并没有发生明显变化.

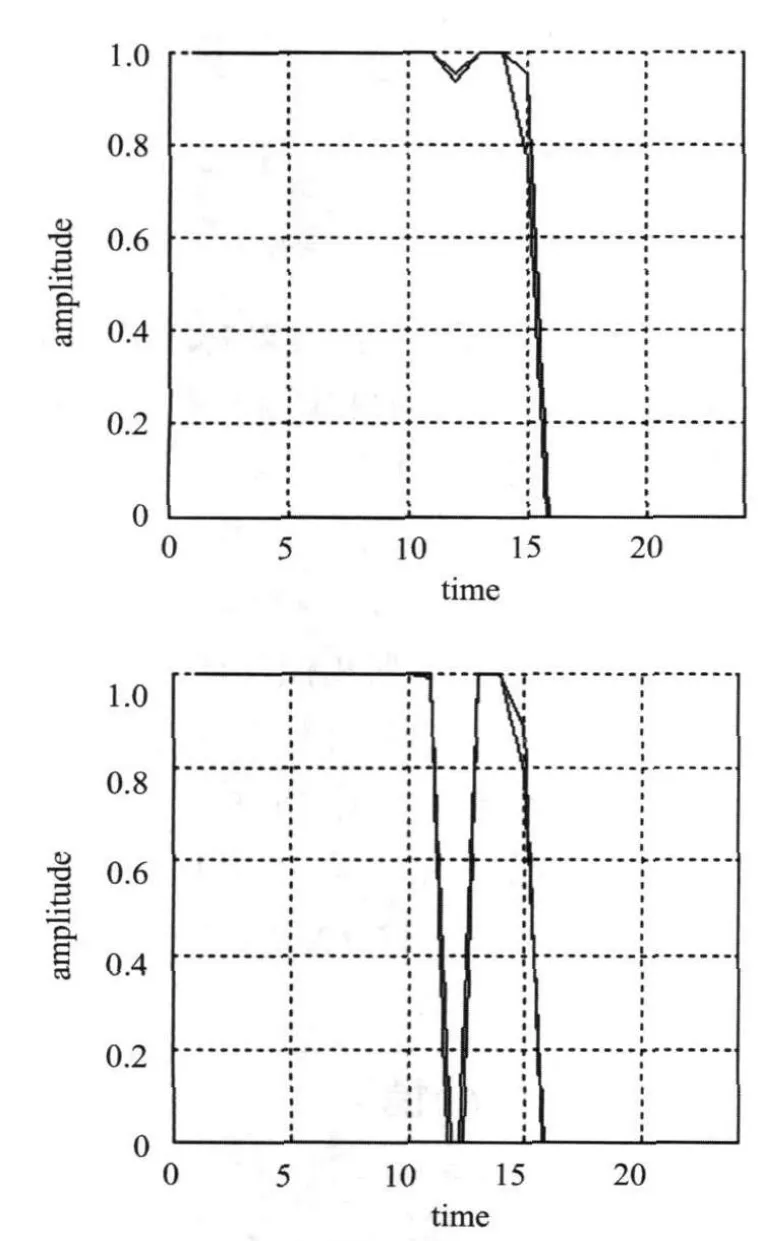
图2 高度相关的节点输出序列

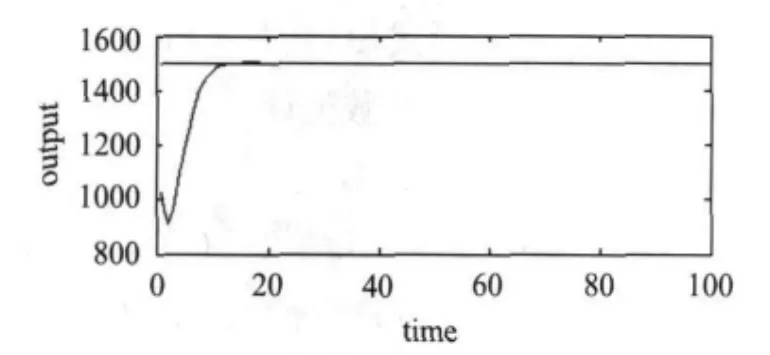
图3 系统输出响应曲线

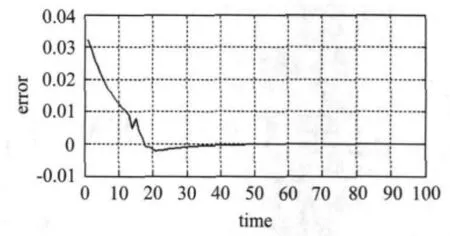
图4 样本学习曲线

4 结论

本文提出了分数阶PIλ控制器中优化BP神经网络的方法，详细介绍了自顶向下的神经网络优化算法.结果表明，自顶向下的优化神经网络方法可以通过合并某些相关性较大的隐节点、删除对网络影响较小隐节点保证神经网络在合并、删除节点后特性不变，从而达到了简化网络结构的目的.

［1］聂冰，赵慧敏，郭永香，等.交流电机调速系统的分数阶 PIλ控制［J］.大连交通大学学报，2012，33(2):84-86.

［2］赵慧敏，李文，邓武.基于神经网络的分数阶PIα控制器的设计与实现［J］.大连交通大学学报，2008，29(1):63-67.

［3］陈东洋，张新政.可变结构神经网络在未来水质参数预测中的应用［J］.科学技术与工程，2008，8(6):1577-1604.

［4］刘光中，李晓峰.人工神经网络BP算法的改进和结构的自调整［J］.运筹学学报，2001，5(1):81-88.

［5］魏海坤.神经网络结构设计的理论与方法［M］.北京:国防工业出版社，2005:125-141.

［6］李广军，张晶，曾安平.基于BP神经网络的PID控制器研究［J］.计算机仿真，2009，26(9):128-131.

［7］CHEN YANGQUAN.A new discretization method for fractional order differentiators via continued fraction expansion［C］.2003 ASME International Design Engineering Technical Conferences，September 2-6，2003，Chicago，USA，2003:1-9.