高压往复泵齿轮传动系统设计及其受力分析

2013-09-20鲍君华郑卓颖何卫东刘鹏

大连交通大学学报 2013年1期

鲍君华，郑卓颖，何卫东，刘鹏

(1.大连交通大学机械工程学院，辽宁大连 116028;2.大连里瓦泵业有限公司，辽宁大连 116600)*

0 引言

往复泵是一种高效节能的流体输送设备，在石油开发、水利水电、矿山开采等领域起着重要的作用［1］.往复泵利用工作腔容积的周期性变化输送高压流体，通常由动力端与液力端两部分组成;液力端把机械能转换为液体的压力能，而动力端则将原动机的能量传给液力端.动力端主要由曲柄、连杆和十字头等部件组成，其实质相当于多个曲柄滑块机构，十字头即为滑块［2］.曲轴是往复泵中的关键部件，其几何形状复杂，工作中承受着强烈的交变载荷，应力集中现象严重，极易发生疲劳破坏［3］，在高压情况下，往复泵中采用正偏置结构的曲柄滑块机构可减小十字头与导板的正压力和摩擦力，从而延长两者的寿命;而动力端的曲柄滑块机构中各杆件尺寸的不同组合将直接影响往复泵的动力性能.因此，结合本文具体的高压往复泵传动系统结构进行分析和设计是十分必要的.

1 传动系统受力分析

1.1 传动方案

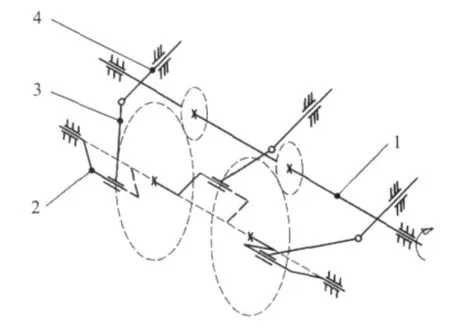
图1 传动机构结构简图

图2 高压往复泵整体装配模型

该高压往复泵传动系统主要由输入轴1、曲柄轴2、连杆3和柱塞4等几部分组成，如图1所示.为了获得需要的流体流量控制方案，通过合理的选择输入轴1和曲柄轴2上的两对斜齿轮传动的传动比来控制曲柄轴的转动速度，这两对斜齿轮可以采用螺旋角相等的人字齿轮传动方案以抵消在啮合过程中的齿间轴向载荷;在曲柄轴2上按照相位各相差120°形成三组曲柄滑块机构，其滑块即为柱塞4.整机装配结构如图2所示.

由于此传动系统采用三个曲柄结构，其曲柄轴上的力和力矩都不会平衡，因此需要分析在柱塞工作过程中通过连杆作用于曲轴上的周期变化的载荷大小.分析中根据曲轴回转方向定义相位角，以逆时针方向为正:中间曲柄1:∠AB1C1=θ1，曲柄 2:∠AB2C2= θ1+120°，曲柄3:∠AB3C3=θ1+240°，连杆的相位角用αi表示，如图3所示.曲柄长lAB=a，连杆长lBC=b，滑块中心C到曲柄中心A的距离，既滑块行程为c.根据机械原理中机构矢量合成原理有，推导出各连杆相位角αi和滑块中心距曲柄距离c的矢量关系，有:

曲柄1:

曲柄2:

曲柄3:

图3 曲轴矢量关系示意图

1.2 曲柄柱塞受力分析

柱塞结构相当于曲柄滑块机构中的滑块，图4(a)中载荷P为作用在柱塞上的流体压强引起的压力，为方便编程计算定义各柱塞上作用力Pi=J·A·p.其中，p为柱塞压力;A为柱塞作用面积;J为控制函数，曲柄正行程阀门打开时，压强p作用于柱塞上，相反曲柄反行程阀门关闭，柱塞上压强p为0;所以当sinθi＞ 0时取J=1，sinθi≤0时取J=0.

图4 曲柄滑块系统受力分析

考虑到传动系统在较良好的润滑状态下工作，为了简化计算忽略运动副间的摩擦力.通过受力分析，图4(b)滑块4上受到柱塞作用力P、连杆3给其的反力Fbc和柱塞缸体对柱塞的支反力Fdc的作用，在此三个力作用下处于力的平衡状态，有根据矢量关系推导出三个柱塞各运动副支反力:

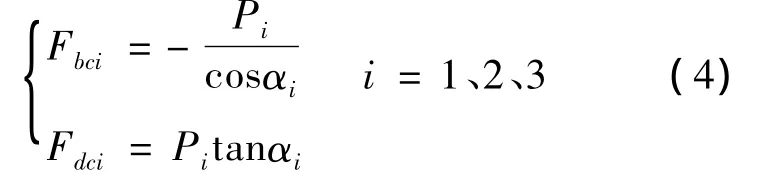
在忽略摩擦和惯性力的条件下，根据图4(d)、(e)分析，连杆BC为二力杆，有Fbc=Fcb=Fab=Fba=Fda，所以连杆BC作用在曲柄AB上的作用力既力的大小相等方向相反.

1.3 曲柄轴及电机轴受力分析

由于主从动齿轮轴线不在水平面上，所以将齿轮副间的圆周力Ft和径向力Fr分别向水平X向和铅垂Y向投影，将此二力合成成Fnx和Fny表示，定义齿轮副安装角γ如图5所示.并推导得出Fny=Ftcosγ +Frsinγ，Fnx=Frcosγ -Ftsinγ，其中:图中此2力对于从动齿轮规定Fny正方向为Y轴负方向，Fnx正方向为X轴正向;主、从动齿轮间为作用力和反作用力关系，主动轮受力分析所列力的方向与从动轮相反，大小相等.

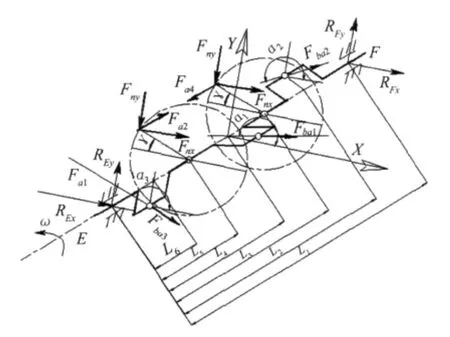
图5 曲柄轴受力图

(1)曲轴受力结果

根据曲轴各力关系，绘制受力简图，如图5所示.其X方向合力为零，即ΣFX=0:

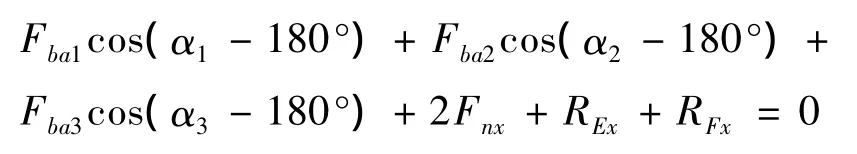
Y方向合力为零，即ΣFY=0:

X方向力矩平衡:对E点列力矩平衡方程有ΣMx(E)=0，顺时针为正.

Y方向力矩平衡:对E点列力矩平衡方程ΣMY(E)=0，逆时针为正.

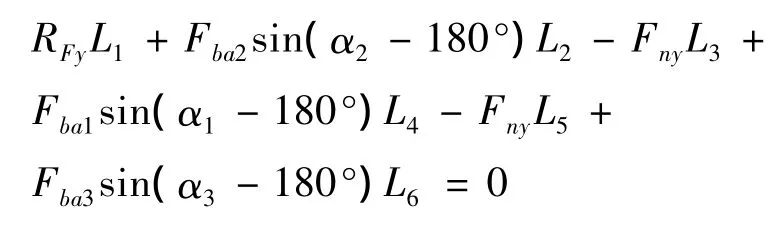
根据上述各式求E、F两点支反力:

(2)电机轴(主动齿轮轴)受力分析

主动齿轮轴转向为顺时针，作用力的方向与从动齿轮方向相反，大小相等.根据各力作用关系列方程如下.

图6中X方向力平衡ΣFX=0:-2Fnx+RAx+RBx=0.

图6 电机轴及齿轮副受力图

Y方向力平衡ΣFY=0:2Fny+RAy+RBy=0.

X方向力矩平衡:对A点列力矩平衡方程ΣMx(A)=0，顺时针为正.

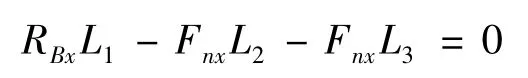
Y方向力矩平衡:对A点列力矩平衡方程ΣMY(A)=0，逆时针为正.

根据上述各式求A、B两点支反力:

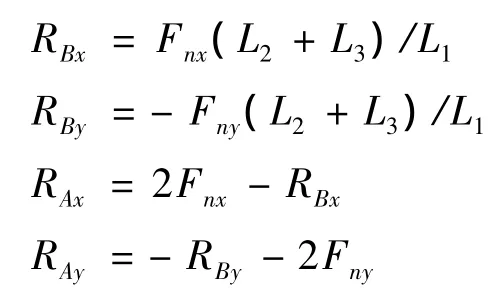
通过以上推导可以计算出电机轴和曲轴上各点的作用力和弯矩值，为强度计算和结构设计提供依据.

2 校核计算

根据曲轴支反力和其上作用的齿轮啮合力分别推导曲轴上各点的弯矩.由图3并根据柱塞工作特点，当曲柄处于图示的第一、二象限时，即正行程时，柱塞上才作用有压力，因此当计算对应曲柄上的反力Fbai不为零，根据几何关系该力与曲柄端点速度方向的夹角为|α-θ-90°|，则其对曲轴上作用的工作阻力矩计算公式为:Ti=Fbai·a·cos(α -θ-90°).通过对弯曲和转矩的推导获得曲轴上各点的当量弯矩计算公式，结合已知的曲轴结构尺寸对危险截面的应力进行了编程计算，计算结果见图7所示.

图7 曲轴及齿轮轴弯矩扭矩计算程序及结果

将已知计算参数代入计算程序，获得曲轴和电机轴弯矩计算结果见表1所示.对于样机涉及的两个传动方案，方案一计算结果求得曲轴上工作最大阻力矩T=831.1 N·m，曲轴上所需驱动功率P=T·n2/9 550=21.83 kW.根据方案二计算结果求得曲轴上工作最大阻力矩T=831.1 N·m，曲轴上所需驱动功率P=T·n2/9550=19.67 kW.这两个功率结果都远远小于电机额定输入功率，所以，齿轮和电机的承载能力都满足设计要求.

表1 曲轴弯曲强度计算结果

曲轴在工作过程中同时承受弯矩和转矩的作用，属于复杂应力状态，应用轴类零件弯扭校核公式，求得合成弯矩，转矩按照脉动循环考虑，取α=0.6.

根据工厂提供的曲轴材料，查得材料的静强度极限应力σlim=σs=590 MPa，疲劳强度极限应力σlim=σ-1=370 MPa，根据危险截面轴段尺寸参数，查取零件绝对尺寸系数εσ=0.64，表面状态系数β=1，应力集中系数Kσ=2.2，计算得到零件许用静应力，疲劳强度许用应力=107.6 MPa，根据上表计算结果曲轴危险截面应力满足强度要求.

齿轮轴在工作过程中也同时承受弯矩和转矩的共同作用，属于复杂应力状态，应用轴类零件弯扭校核公式，求得合成弯矩表2给出了计算结果.

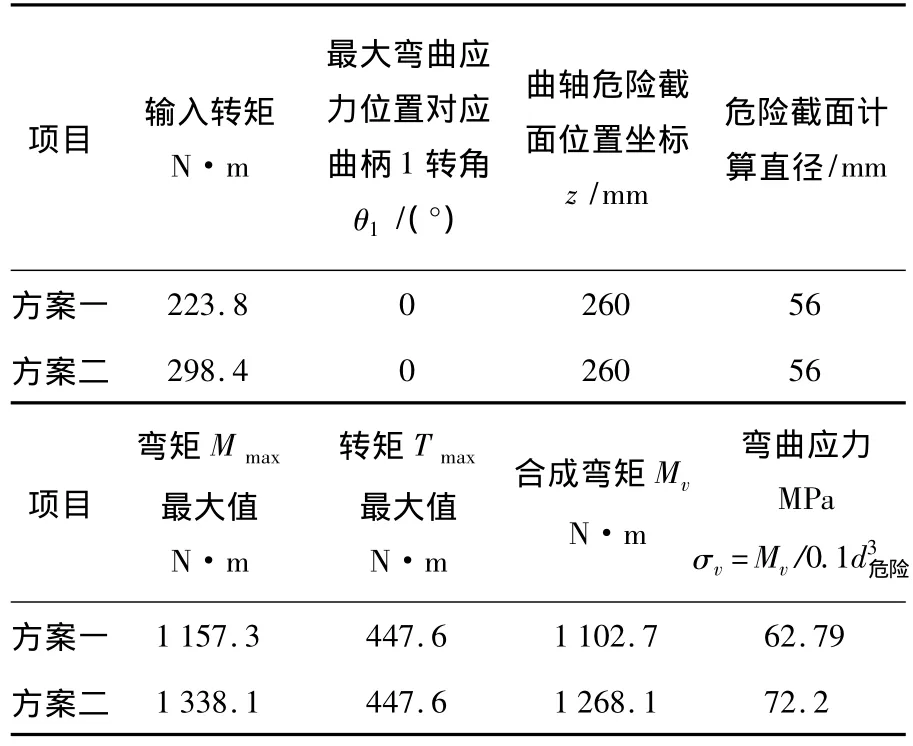
表2 齿轮轴弯曲应力计算结果

齿轮轴材料和主动齿轮相同，查得材料的静强度极限应力σlim=σs=1 080 MPa，疲劳强度极限应力σlim=σ-1=551 MPa，根据危险截面轴段尺寸查取零件绝对尺寸系数εσ=0.7，表面状态系数β=0.8，应力集中系数Kσ=2.11，计算得到零件许用静应力，疲劳强度许用应力2 MPa，根据上表计算结果齿轮轴危险截面应力满足强度要求.