建构主义理论在数学教学中的应用

王德瑞

（甘肃民族师范学院，甘肃 合作 747000）

建构主义理论认为，知识不是通过感觉或交流被个体被动接受的，而是由认知主体主动建构起来的，建构是通过新旧经验的相互作用而实现的[1]。这说明在教学过程中，教师不能将知识硬灌输给学生，只能引导学生积极开展探索、研究和讨论等活动，并通过学生的探索研究，学生与学生、教师与学生间的相互交流，让学生发现、掌握新知识，积累新经验，同时不断增强学生的合作交流意识，提高学生的学习能力。

笔者在甘南藏族自治州的合作市和夏河县指导学生实习时，利用建构主义的教学理念，对初中数学教学进行了实验研究。通过实验，笔者认为将建构主义理论贯穿于藏族地区的数学教学，是富有成效的，它对于学生掌握知识、增强创新意识、提高探索研究能力，具有非常重要的现实意义。

在实验研究中，主要做了以下几方面工作。

1 引导学生探索研究和讨论，主动构建

从建构主义的观点来看，学生在学习数学的过程中不是外界信息刺激的被动接受者，而是知识意义的主动建构者[2]。因此，在教学过程中应让学生通过探索研究来获得知识，而不是直接向他们传授知识。

笔者根据上述建构主义教学理念，引导学生进行探索研究和讨论，使他们主动建构知识，取得了良好效果。例如，在讲授“三角形内角和定理的证明”时，大多数教师仍利用课本所述的证题方法引导学生进行证明，甚至将课本中的证题方法直接传授给学生，忽视了学生对证题思路的探索研究。可我们在实验研究时发现，学生解决问题的思路不拘一格。教师提出问题后可让前后两桌4名学生为一组进行讨论（全班46人，可分为12组），学生在讨论后提出以下几种证法：

（1）延长△ABC 的一边BC 至D，过点C 作直线CE∥AB（如图1），则∠BAC+∠ABC+∠ACB=∠ACE+∠ECD+∠ACB=180°（5个小组提出）。

（2）过△ABC 的一个顶点A 作直线EF∥BC（如图2），则∠BAC+∠ABC+∠ACB=∠BAC+∠EAB+∠FAC=180°（4 个小组提出）。

（3）过点 A 作直线 AD∥BC（如图 3），则∠BAC+∠ABC+∠ACB=∠BAC+∠ABC+∠DAC=∠ABC+∠BAD=180°（2 个小组提出）。

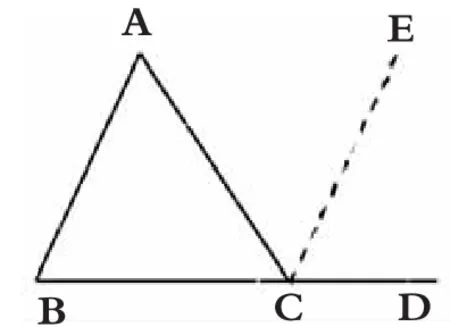
图1

图2

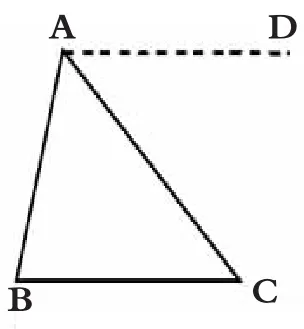
图3

（4）过边B C 上一点D分别作直线D E∥A B、D F∥A C（如图 4），则可推知∠B A C+∠A B C+∠A C B=∠E D F+∠E D C+∠F D B=180°（1个小组提出）。

（5）过△ A B C 内一点O 分别作直线E F∥ B C、G H∥ A B、M N∥A C（如图 5），则可推知∠ B A C+∠ A B C+∠ A C B=∠ 1+∠ 2+∠ 3=180°（2个小组提出）。

（6）过△ A B C 外一点O分别作直线E F∥ B C、G H∥ A B、M N∥A C，使得直线E F 与A B、A C 边的交点分别为E 和F，A C 或其延长线交G H 于H（如图6），则可推知∠B A C+∠A B C+∠A C B=∠1+∠ 2+∠ 3=180°（3个小组提出）。

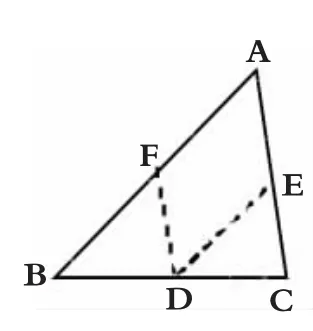
图4

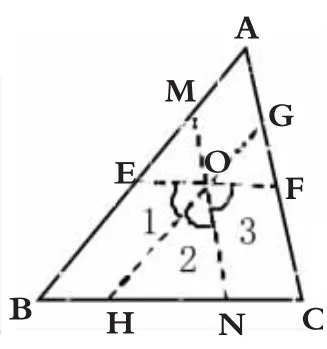
图5

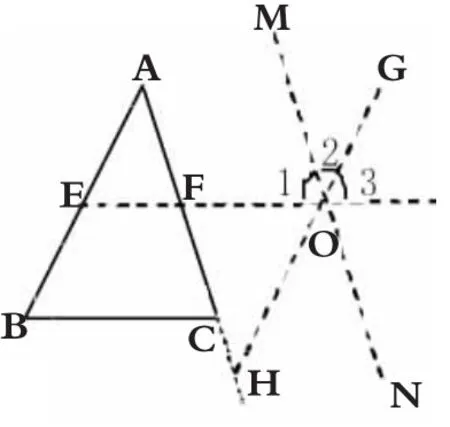
图6

其中有些小组同时提出两种以上证法，还有一些学生提出“先证三内角和的两倍等于360°”、“先证三内角和的一半等于90°”等方案，但没有找到证明的具体方法。

提出上述前两种证法的学生较多，而这两种证法也恰是课本所提供的，这可能是有些学生因课前预习得知，而其他各种证法，都是学生根据自己已有的知识基础通过探究而提出的。

由上述例子可知，学生对解决问题的策略都有各自的见解，如果教师引导学生积极主动开展探索研究和讨论活动，并进行点拨和总结，会使学生在掌握知识的同时，开阔视野，提高分析问题和解决问题的能力，从而使课堂教学达到事半功倍的效果。

2 通过数学活动，建构数学概念

如前所述，学生在学习数学的过程中不再是外界信息刺激的被动接受者，而是知识意义的主动建构者。所以，对于数学概念，也应让学生通过一定的数学活动来理解和掌握，而不能通过直接传授使学生被动接受。

例如，多数教师在讲授“三角形的高线”概念时，将定义直接传授给学生，即结合图形向学生说明：从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足之间的线段叫做三角形的高线，讲述时所画图形中的高线也往往在三角形的内部。因此，有些学生虽能熟记定义，但没有真正理解定义，在钝角三角形中作不出钝角边上的高线，也不知道直角三角形直角边上的高线所在的位置。针对这种情况，笔者指导学生设计了一个数学活动情境：首先，让学生画一个钝角三角形并分别从所画三角形的各个顶点向它的对边所在直线作垂线。学生在画图过程中可以相互交流、讨论，教师巡回检查，必要时与部分学生交流和讨论。待学生画出图形后，教师给出“三角形的高线”的定义，并提出：在钝角三角形中有几条高线？其中哪些边上的高线在三角形的内部？哪些边上的高线在三角形的外部？经师生共同讨论总结得出结论。其次，让学生画出直角三角形各边上的高线并讨论以上问题。通过以上数学活动，使学生最大限度地参与到探究新知识的过程中，使他们主动建构数学概念，达到深刻理解的目的。

这说明，在课堂上以数学活动为主旋律贯穿始终，使学生在动手操作中建构数学概念，是数学概念教学中非常有效的策略。

3 引导学生积极开展讨论交流活动

建构主义把交互性看作是学习的关键，因而建构主义下的教学过程就是教师与学生、学生与学生间的多边活动[3]。因此，教学中应以对话、沟通的方式，让大家提出不同的看法来刺激个体思考，通过质疑、反思来澄清疑虑，逐渐完成知识的建构，进一步掌握知识。

例如：甲袋中有两个红球一个白球，乙袋中有一个红球一个白球，两袋中各取一球，求所取两球都是红球的概率。经课内讨论，1/3 的学生认为概率是1/4，因为取球结果有“红红、红白、白红、白白”4 种；1/4 的学生认为概率是1/3，因为取球结果有“红红、红白、白白”3 种；其余学生认为取球结果有“红红、红白、红红、红白、白红、白白”6 种，所以概率是2/6，即1/3。针对第二种见解，教师提出“一红一白是怎样取得的？”学生经过讨论后普遍认为是由甲袋中取一红球，乙袋中取一白球，或由甲袋中取一白球后乙袋中取一红球而得，因此这种取法可列举为“红白、白红”两种，这说明第二种见解是错误的。接着一名学生提出第一种见解也是错误的，因为第一种见解刚好是在甲袋中也只有一个红球和一个白球的结果。随后经教师点拨，学生利用不同的方式得出了两种列举结果：“红红、红白、红红、红白、白红、白白”和“红红、红红、红白、白红、白红、白白”，由这两种列举法求得的概率均为1/3。

这说明，在教师的指导下，学生利用讨论交流的方式不断反思、重建自己的认知结构，不但弥补了原有认识中的不足，改正了错误，而且还开阔了思路，提高了解决问题的能力。

值得注意的是，虽然许多专家认为建构主义是促进素质教育、推动数学教学改革的重要理论，且建构主义理念下的数学教学改革也取得了可喜成果，但是，目前，这种改革在西部民族地区仍无较大进展。主要原因是：第一，受传统教育理论的影响，多数教师没有树立起建构主义教学理念，至少对建构主义理论没有引起足够的重视；第二，尽管一些教师根据建构主义理论进行了教学改革试验，但由于改革不得法，导致收效不大，甚至以失败告终。所以，要组织教师学习建构主义理论知识，将建构主义理论知识渗透到师范院校教学论课程之中，同时通过技能培训、进修、在校学习等途径，使数学教师掌握必要的建构主义理论知识，树立建构主义教学理念。教师在教学中要灵活运用建构主义教育理论，不怕吃苦、费神，根据学生的知识基础和生活经历，精心设计教学方案，开展课堂教学活动。

[1]张秀梅，高洪伟.建构主义理论在高职数学教学中的应用[J].科学教育，2008（6）：128.

[2]曹一鸣.数学教学模式导论[M].北京：中国文联出版社，2002.

[3]涂荣豹，喻平.建构主义观下的数学教学论[J].南京师大学报：社会科学版，2001（3）：80.■