光纤数值孔径与衰减系数的测量实验

曲天良，卢广锋，肖光宗，石丽芬

（国防科学技术大学，湖南 长沙 410073）

光纤在现代光通信领域得到广泛的应用，数值孔径和衰减系数是光纤的重要参数。最早用光来传递信息的通讯方式是海上灯塔和长城上的烽火，但是这些通讯方式很容易受天气影响。第一项用于光通信系统的专利在1880年被提出，AlexanderGraham、Bell等研制了光电话实现200m距离光束通信。1910年Hondros和Debye提出一种电介质波导理论，使光纤波导被选定为目前和未来通信传输介质的杰出竞争者。1966年2位科学家CharlesKao和George A.Hockham计算推测：如果光纤的千米传输效率达到1%，那么光纤波导就能够和当时用于通信的同轴光缆相竞争。值得注意的是，当时最好的光纤其透射光能在20m后就降到1%，没有材料专家曾预言光纤能达到如此高质量的光传输效率。尽管如此，很多研究组开始积极探索这种可能性。1970年Corning玻璃公司研制了高硅玻璃光纤，首次报道了其在1km距离透射大于1%，今天已实现1km距离透射达95%～96%。信息携带量大，抗电磁干扰，尺寸小，重量轻等优越性创造了一项崭新的技术，光纤成为通信应用的选定介质。因为光纤光学系统的设计者需要知道有多少光能耦合到光纤里面以及在传播一给定距离之后还有多少光保留在光纤中，因此光纤最重要的规格说明是数值孔径和衰减系数。因此很有必要设计光纤光学的实验，测量光纤的数值孔径和衰减系数，加深学生对光纤基本概念的认识［1－6］。

1 实验原理

___数值孔径NA是光学系统收集光的能力的度量标准，这个光学系统可能是光纤、显微镜物镜或摄影镜头。数值孔径是入射介质的折射率和最大入射光线角正弦的乘积：

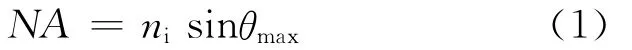
在大多数的情况下，光是从空气方面入射，ni＝1。阶跃光纤纤芯的折射率是常数，并且在纤芯—包层界面，折射率发生突变。从光纤的截面可以看到被光纤所接收的光锥是由芯和包层之间的折射率差所决定。折射率差由下式给出：

图1 阶跃光纤（右边是折射率剖面图）

如图1所示，光线以临界角入射到纤芯 －包层界面。如果光锥角是θc，按Snell定律：

由于sinθcrit＝ncl／ncore，所以

由公式（1）、（4）得到阶跃光纤的数值孔径

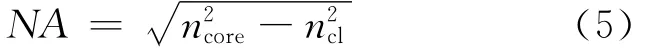
当Δ≪1时，方程（5）可近似为

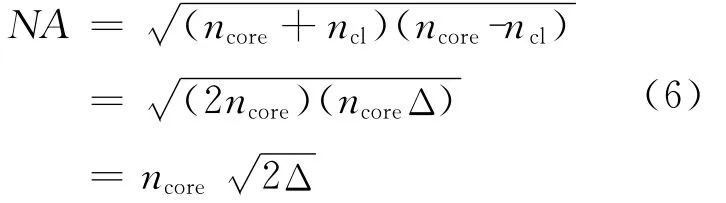
当Δ≪1是弱波导近似的情况。光纤的数值孔径在实验中进行测量。典型的多模通信光纤Δ≈0.01，即Δ≪1，对弱波导近似当然是合理的。对硅制备的光纤ncore近似1.46。用方程（6），Δ和ncore值算出NA＝0.2。单模光纤的NA值约为0.1，多模通信光纤的NA值在0.2～0.3之间，大芯光纤的NA值约为0.5。

下面介绍光纤衰减的测量原理。在光纤中传播距离z后仍然保留的光功率的表达式为I（z）＝I（0）10－（Γz／10），光纤的长度z用km给出，衰减系数以每千米分贝给出（dB／Km）。原则上，光纤衰减测量是所有光纤测量中最容易做的。通用的方法称为“截短法”，就是从光源发射功率到一段长度的光纤中，用线性响应的探测器测量光纤远端接收的功率，然后切去一段长度的光纤，测量被截短长度光纤所传输的功率。在系统的入射端留下一段短长度光纤的原因是保证所被测量的损耗仅是由于光纤的损耗而不是当光源耦合到光纤所发生的损耗，图2是测量系统的图解说明。

图2 测量光纤衰减的截短法的试验装置图

设长度为z的光纤的透射率为T＝Pf／Pi，这里用Pi（初始功率）和Pf（最后功率）来分别代替I（0）和I（z）。用分贝表示的损耗的对数表达为L（dB）＝ －10log（Pf／Pi），负号使损耗表示为正数。当用对数表达时，允许损耗相加，然后从初始的功率减去。用dB／Km表示的衰减系数 是损耗L除以光纤长度z。衰减系数由下式给出Γ（dB／Km）＝ （1／z）［－10log（Pf／Pi）］。总的光纤衰减是衰减系数乘光纤长度，用分贝（dB）表示的对数形式表达。

2 实验装置及结果

图3表明一种测量光纤NA的方法。激光器发出的平面波沿z－方向传播。激光束的宽度约为1mm，这比光纤直径100μm大很多。当平面波入射在光纤端面上时，所有发射到光纤中的光有相同的入射角θc，如图3所示。如果光纤端面绕着图3中的O点旋转，可以测量光纤所接收到的光功率随入射角θc的变化。使用该方法可以测量光纤的数值孔径（NA）。

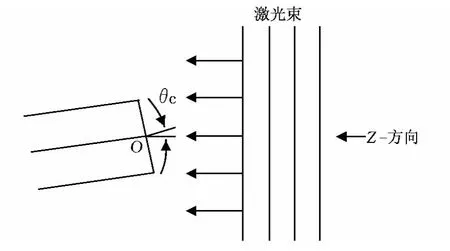
图3 激光束平面波进入光纤的几何图示和实验装置

图4表明使用上述方法测量的Newport F－MLD光纤所接收的光功率随入射角的变化。当接收功率降到特定值，该点对应的角度即为光锥的最大入射角，用于计算NA。美国电子工业协会采用的特定值规定为，接收功率是峰值接收功率的5%时的入射角为最大入射角。选定5%强度点是为了降低背景噪声的折衷方法。

图4 测量Newport F－MLD光纤NA的数据图示

注意，在图4中接收功率测量是对光纤正、负转动进行的，数值孔径NA是由两个5%强度点之间全角的一半来确定的。这样将消除对平面波激光束进行准直（θc＝0）时所带来的小的偏差的影响。这种实验情形下所得到的NA是0.29，和制造厂商的规格NA＝0.30相近。

用截短法测量光纤衰减系数的实验设置如图5所示。制备F－WLD－500光纤线圈的两个端面。光纤纤芯为100μm，直径为140μm。将切割好的光纤远端放置到裸光纤夹持器，然后将裸光纤夹持器插入到与光功率计探头相连的光纤适配器中。使用光纤耦合器将 He－Ne激光耦合入光纤。将He－Ne激光对准耦合器以便激光光束沿着光纤耦合器的轴。仔细地准直光纤以达到发射到光纤中的光为最大，采用功率计以监控发射功率。在与激光束45°角的位置放一个显微镜载玻片玻璃，观测从光纤端面来的Fresnel反射。通过调整光纤位置的z坐标，聚焦Fresenl反射光束，调整光纤固定器上z方向旋钮完成这步。当该反射被聚焦时，则光纤端面在耦合器显微镜物镜焦平面上。测量光纤远场的输出功率，注意光纤的精确长度，它是光纤线圈标签的部分资料。从扰模器后截下2m长光纤，切割光纤的截断端，并从截断段测量输出。用公式Γ（dB／Km）＝ （1／z）［－10log（Pf／Pi）］计算光纤衰减系数，把此结果和线圈上所标明的光纤资料上的衰减系数相比较。

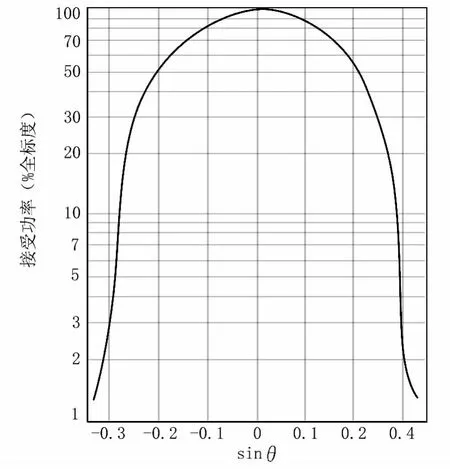
图5 用截短法去定义光纤衰减的实验设置

3 结 论

光纤在光通信领域起到举足轻重的作用，光纤光学是一门新兴的充满活力的学科，开设光纤实验课程十分必要，尤其是测量光纤的数值孔径和衰减系数等基础实验。搭建了实验系统，准确测量了光纤的数值孔径和衰减系数。该实验能够提高学生的实验能力，加深对光纤的数值孔径和衰减系数等基本概念的认识。

［1］D.Kalish，et al.Fiber Characterization－Mechanical.Optical Fiber Communications，S.E.Miller and A.G.Chynoweth，eds，Academic Press（New York），1979：406.

［2］D.Gloge and W.B.Gardner，Fiber Design Considerations.Optical Fiber Communications，S.E.Miller and A.G.Chynoweth，eds..Academic Press（New－York），1979：152.

［3］TIA／EIA Standard 455－47B，Section 6.1，2，EIA，Engineering Dept.（Arlington，VA），1992.

［4］D.L.Franzen and E.M.Kim，Interlaboratory Measurement Comparison to Determine the Radiation angle（NA）of Graded－index Optical Fibers.Applied Optics 20，p.1220（1981）.

［5］D.Marcuse.Principle of Optical Fiber Measurement.Academic Press（New York），1981：226－236.

［6］赵瑞娟，安盼龙，张旭峰，等.快速耦台光纤过程与半导体激光器电光特性实验的研究［J］.大学物理实验，2013，2：4－6.