两种驾驶员方向控制模型的比较研究

沈 峘，谭运生，马爱静，金智林

(南京航空航天大学能源与动力学院，南京 210016)

驾驶方向控制模型将驾驶员的操纵行为用数学模型来描述，结合仿真技术代替真实驾驶员完成对汽车的操纵，便于在汽车V字形开发流程的初期进行闭环评价。该模型的建立不但能有效地缩短开发周期、降低开发成本，而且较试车员场地测试具有更好的可重复性和试验安全性。从早期的汽车操稳性评价，到汽车安全系统的控制策略开发，再到现阶段汽车自主/辅助驾驶系统的探讨，准确地描述驾驶员的操纵行为，并建立与驾驶员具有良好一致性的驾驶员模型一直是研究关键。总体来看，驾驶行为建模主要分为纵向和横向控制2大类。纵向控制是为了保持安全的车间距或者定速巡航等功能而设计［1］;横向控制主要是通过调整方向盘来维持车辆稳定地行驶在道路中心，这类问题又被称为驾驶员方向控制或转向控制［2］。

就驾驶员方向控制而言可分为补偿控制模型和预瞄跟踪模型2种。2种模型都假定驾驶员通过注视道路前方某一点或部分区域来获取信息，并据此决策方向盘转角。区别在于，前者直接将注视点处的信息与当前车辆运动状态进行比较来获取偏差量，以此决策出控制输入;而后者先通过预瞄估计出车辆行驶到此处时的运动状态，再将该状态与预期道路比较形成偏差量来决策方向盘调整角。由于考虑了预瞄环节，因此较补偿控制模型更接近于实际情况。然而，由于现实中驾驶环境、驾驶员行为的复杂性，以及车辆本身的非线性、时滞等因素，至今没有形成完整、统一的驾驶行为建模理论体系。文献［3-4］对现有的建模方法进行了详细的综述，而本文则从另一角度出发，选取具有代表性的方法进行分析和对比，以便更好地理解人车闭环系统，为建立更加完善的驾驶员方向控制模型提供参考。

1 建模方法

驾驶员建模的研究可以追溯到20世纪50年代，当时的研究侧重于理解和评价车辆的动力学特性。自20世纪60年代起，驾驶员和车辆被当作一个整体来研究，驾驶员的生理、心理特性等因素也开始被加以考虑。经过半个多世纪的发展，涌现了大批优秀的建模方法［5-7］。通过对大量文献的调研发现，其中2种较为典型的建模方法值得深入分析和对比。下面将对这2种方法进行简要介绍。

1.1 预瞄-跟随模型

预瞄-跟随模型(preview follower，PF)由我国郭孔辉院士提出，该模型由于物理概念清晰，跟随精度较高，已获得广泛的应用［8］。参考图1所示的单点预瞄示意图，该模型假设驾驶员根据当前时刻的汽车运行状态预测出到达预瞄点B后的位置，并与预瞄点f(t0+T)进行比较，获得侧向偏差;再根据运动学原理，以及方向盘转角与道路的几何关系推导出消除侧向偏差的最优曲率或最优侧向加速度;然后，驾驶员根据对汽车侧向动力学特性和自身生理滞后特性的了解将理想的侧向加速度转化为方向盘调整角，使汽车行驶到预瞄点B后能与目标轨迹f(t0+T)重合。

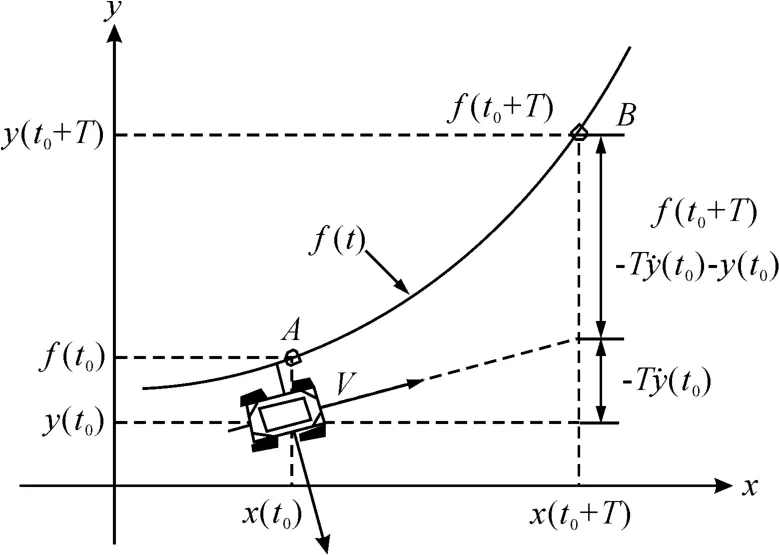
图1 单点预瞄示意图

预瞄跟随系统的具体结构如图2所示。其中:T为预瞄时间;V为车速;Th为手臂延时;τ为神经延时;C(s)=c0(1+Tcs)为驾驶员的二阶校正环节;c0和Tc分别为驾驶员校正环节的比例和微分增益，与汽车的动力特性有关。

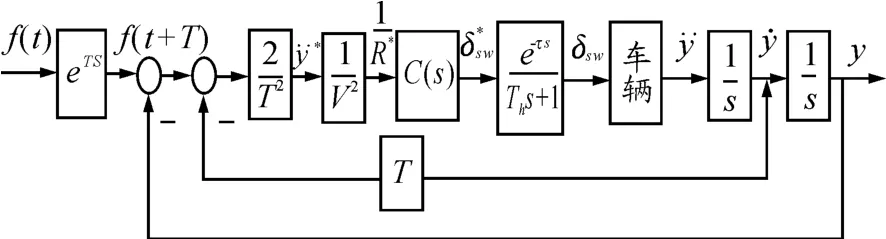
图2 预瞄跟随模型

1.2 NMS-QR 模型

另一个被广泛应用的模型由Macadam提出，称为预瞄最优模型(optical preview control，OPC)，由于采用了最优化技术，因此所形成的理论较为严密、有效。该模型通过将侧向跟踪偏差最小化来优化方向盘转角，没有考虑横摆角偏差。随后，Sharp等人同时考虑了侧向位移偏差和横摆角偏差，并将其发展为多点预瞄模型，采用LQR方法求解。最近，由于各种先进转向系统，如电动助力转向系统、线控转向系统的出现，迫切需要理解和考虑驾驶员手臂和方向盘的动态交互作用。Cole等在LQR模型的基础上提出了基于手臂肌肉系统(neuromuscular system，NMS)的驾驶员方向控制模型，本文简称为 NMS-LQR 模型［9］。NMS-LQR 模型的结构如图3所示。其中:Ka为手臂的刚度增益;Hr(s)为手臂的反射控制单元;Gs(s)为手臂与方向盘耦合的传递函数。计算方法如式(1)所示。

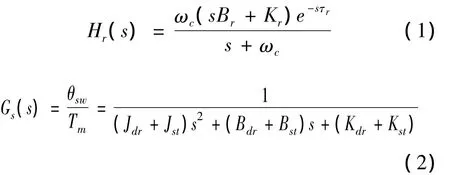
式(1)、(2)中:Jst、Jdr分别为方向盘和手臂的转动惯量;Bst、Bdr分别为方向盘和手臂的阻尼;Kst、Kdr分别为方向盘和手臂的刚度;Kr、Br分别为反射刚度和阻尼;ωc为系统的截止频率;τr为神经传递延时。

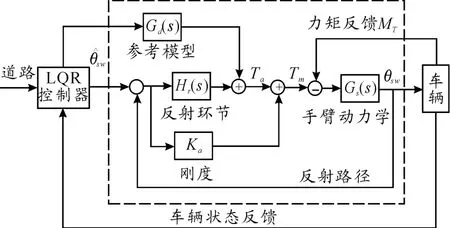
图3 NMS-LQR结构

采用LQR控制器的设计方法，假设车辆2自由度侧向动力学模型的离散形式为:

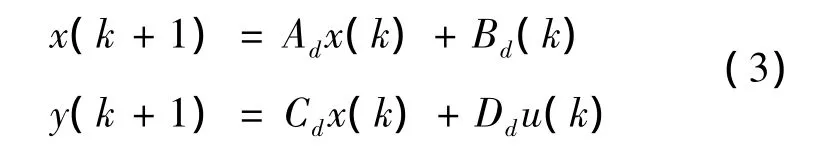
将多点预瞄偏差信息与车辆动力学模型组合，并用标准状态空间形式表示为:

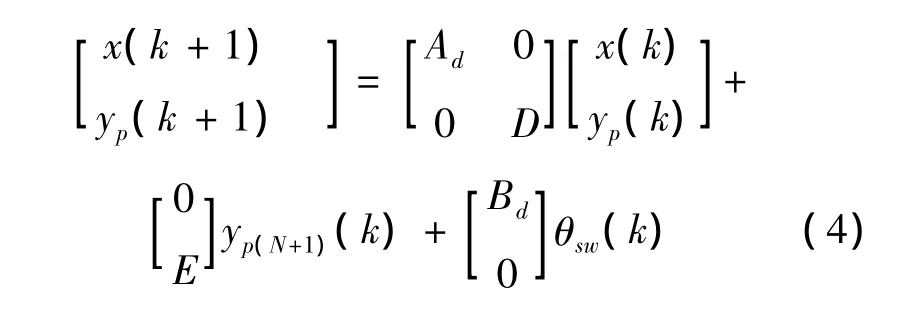
其中:

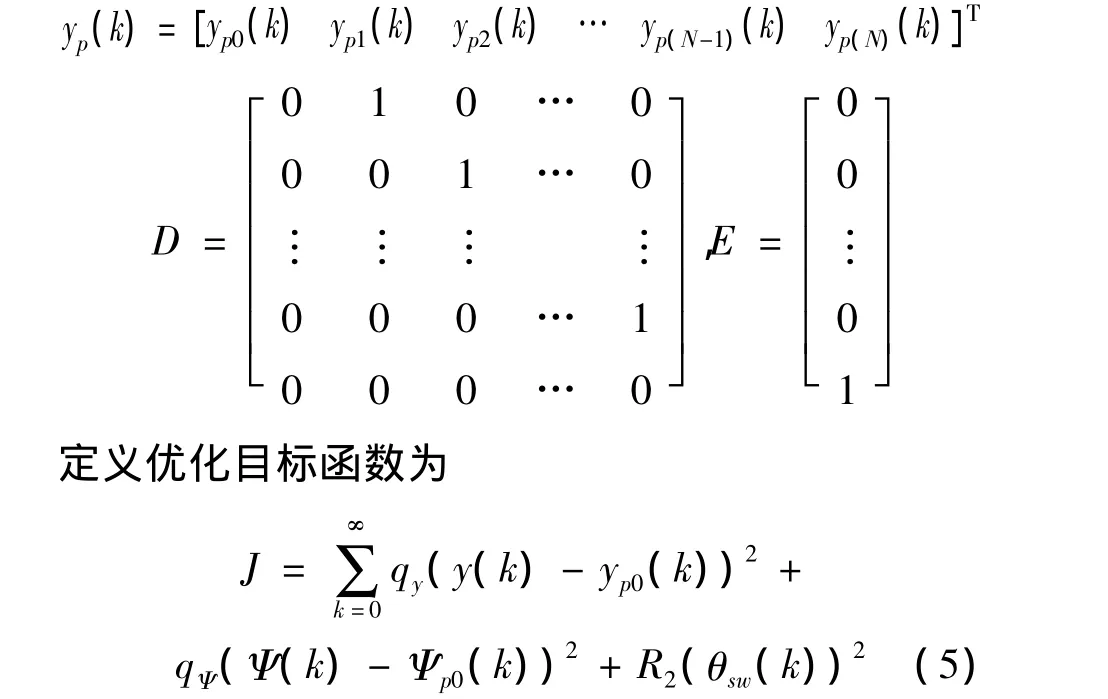
其中:qy和qΨ分别为侧向和横摆角偏差的权值;R2为控制量的权值。

将式(5)转化为矩阵形式，有

通过LQR进行求解，可得最优的方向盘转角

其中:Kp=［k1k2k3k4kp1kp2… kpn］;k1～k4分别代表车辆的状态增益;kp1～kpn代表道路预瞄增益。

2 仿真分析

为评估2种驾驶员方向控制模型的路径跟踪性能，选择双移线工况作为道路输入。借助Matlab仿真平台进行分析和比较。表1给出了仿真选用的整车参数以及2种驾驶员方向控制模型相关的参数，其中仿真车速为120 km/h。

表1 参数汇总表

为确定预瞄跟随模型的最优预瞄时间，综合考虑轨迹偏差E、方向盘转速˙δsw和侧向加速度¨y，建立如下综合优化指标:

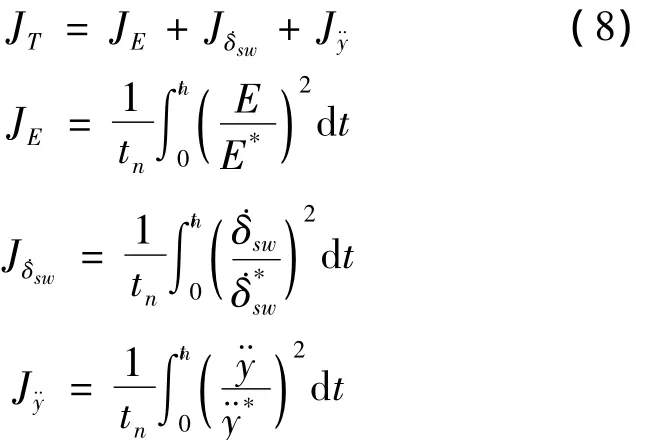
其中E*和分别表示轨迹偏差、方向盘转速和侧向加速度的门槛值。在仿真计算中分别取0.3 m、360(°)/s和 0.3 g。

图4给出了预瞄时间T的范围是0.3～0.9 s，步长为0.1 s时的仿真结果。由图4可知，指标JE随预瞄时间的增加而增大;相反，指标J˙δsw和J¨y随着预瞄时间的增大而减小，这使得综合性能指标JT在0.6 s处达到最小值。因此，在本文的仿真中预瞄时间T取0.6 s。

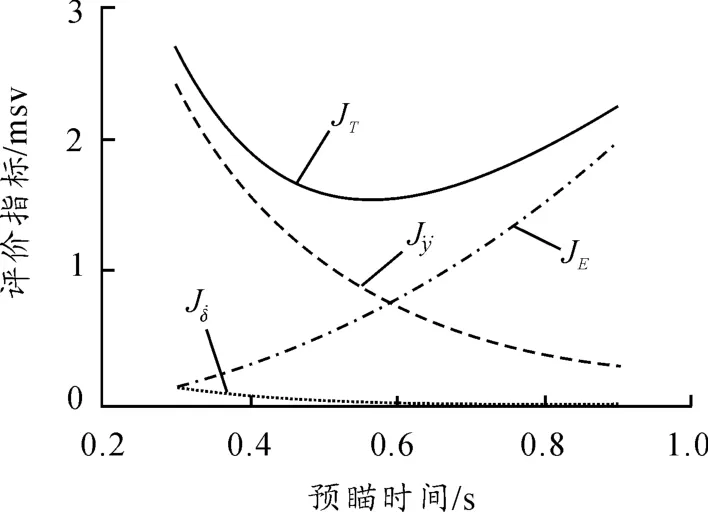
图4 性能指标

与预瞄跟随模型不同，LQR模型采用多点预瞄方式。为计算最优的控制增益Kp，取预瞄范围为0～2 s，采样时间间隔定为0.02 s，这样可以获得100个预瞄点。针对代价函数取不同权值计算出的最优控制增益如图5所示，其中左栏表示状态增益，右栏表示预瞄增益。由图5(a)给出的预瞄增益可以看出，不考虑方向角偏差会导致增益衰减较慢。同理，图5(b)给出的是未考虑侧向偏差的情况，其状态增益明显降低。图5(c)给出的是同时考虑侧向偏差和方向偏差的情况，大约在第60个预瞄点处(约1.2 s处)预瞄增益衰减到零，且具有良好的状态增益，在仿真中获得了满意的控制效果。

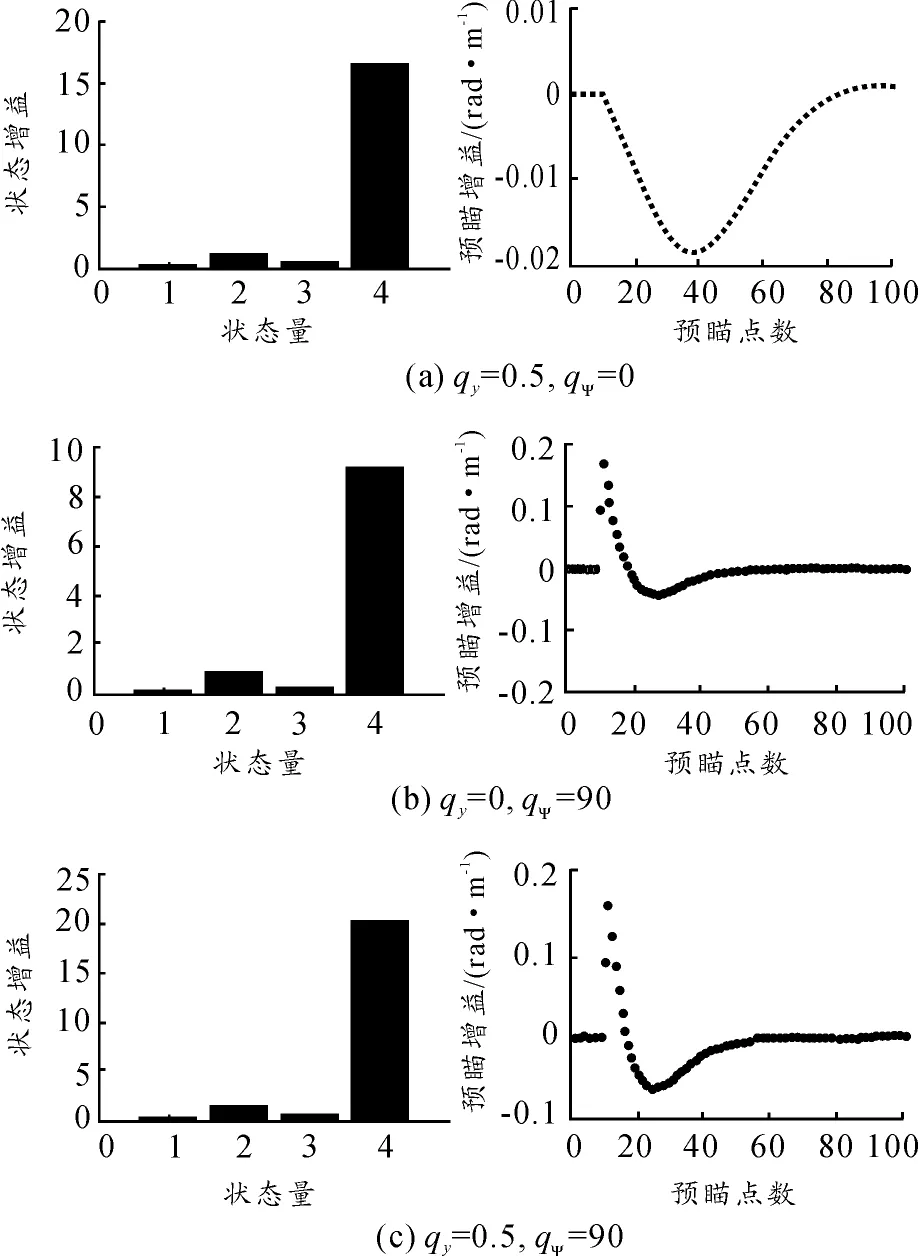
图5 不同权重下的控制增益

2种方法的路径跟踪性能如图6所示。由图6可知，2种方法都能很好地实现路径跟踪。相比较而言，LQR的跟踪精度更高，但在其转向后期出现波动(参见图6(d))。如对应实际驾驶工况，则表示较大的转向增加了驾驶员的负担，因此驾驶员转向操纵紧张，容易出现转向疲劳。而预瞄跟随模型在整个转向过程中操纵动作比较平稳，且转向角较小。因此，该模型以相对较低的转向负担实现了较为准确的道路跟随精度。

图6 2种模型的双移线仿真结果

综合2种模型的基本原理及分析，将其各自的特点进行归纳，如表2所示。

3 结论

1)闭环仿真结果表明:2种模型均具有良好的路径跟踪性能，同时也具有各自的优缺点，因而需要根据不同的应用进行选择。需要注意的是:2种模型都假定驾驶员采用固定预瞄方式，而实际驾驶员会根据驾驶状态来动态调整预瞄线索，因而自适应预瞄方式是需要继续研究的问题。

2)预瞄跟随模型从模拟人的角度出发，将预瞄信息转化为最优的转向曲率，再通过驾驶员动态校正环节进行跟踪。模型的推导过程不但考虑车辆的动力学原理，还考虑了驾驶员的生理因素，各参数的物理概念明确，但驾驶员实现转向动作仅考虑了一阶惯性环节，因而与实际驾驶员的转向行为还存在差距。

3)基于LQR的模型采用最优控制理论，控制效果较为理想。由于考虑手臂和转向系统的交互过程，经过改进有望用于动态评价近年来出现的先进转向技术，例如电动助力转向系统和线控转向系统。若该模型用于智能/无人车等应用，则存在多点预瞄信息难以获取的困难，此时，单点预瞄信息的获取方式更加可行。

表2 2种模型的原理及特点

［1］丁卫东，柳祖鹏，朱晓宏.车辆纵向运动跟车间距控制的研究［J］.中国机械工程，2004，15(11):1030-1032.

［2］Shen H，Ling R，Mao J G，et al.Steering control strategy guide by two preview vision cues［J］.Science China Technological Sciences，2012，55(9):2662-2670.

［3］Macadam C C.Understanding and modeling the human driver［J］.Vehicle System Dynamics，2003，40(1):101-134.

［4］Plöchl M，Edelmann J.Driver models in automobile dynamics Application［J］.Vehicle System Dynamics，2007，45(7):699-741.

［5］段立飞，高振海，王德平.驾驶员对汽车方向的自适应控制行为建模［J］.机械工程学报，2011，47(8):121-125.

［6］沈峘，凌锐，李舜酩.基于预瞄最优曲率模型的大曲率转向控制方法［J］.中国机械工程，2012，23(17):2111-2116.

［7］Ungoren A Y，Peng H.An adaptive lateral preview driver model［J］.Vehicle system dynamics，2005，43(4):245-259.

［8］Guo K，Guan H.Modelling of Driver/Vehicle Directional Control System［J］.Vehicle System Dynamics，1993，22(3):141-184.

［9］Pick A J，Cole D J.A mathematical model of driver steering control including neuromuscular dynamics［J］.Journal of Dynamic Systems，Measurement，and Control，2008，130(031004):1-9.