拉格朗日插值法在工程设计及CAD中的应用

林昌华，杨 岩

(重庆理工大学机械工程学院，重庆 400054)

工程设计及CAD过程中涉及到大量的数据查询和处理工作。工程设计资料或手册中的数据往往没有公式表达的函数关系，而是以表格或者线图的形式给出，有的待查数据可能处于相邻2个节点数据之间，有的数据则在对应的线图上。如何快速、准确地取出待查数据，实现对设计资料和数据的自动化处理，是高效、精准、快捷完成设计工作的关键。无论是对于表格节点间区域数据的获取或是线图数据的处理，拉格朗日插值法的应用都较好地解决了工程设计及其CAD中的这一问题。

1 插值法及其基本原理

插值法的基本原理:在插值点附近选取若干合适的节点，过这些节点构造一个简单的插值函数y=p(x)，在所选数据区间用插值函数作为原来函数f(x)的近似表达式，然后计算插值函数p(x)的值以代替原函数f(x)的值，使得f(xi)=p(xi)，i=1，2，3，…，n成立。由此可见，插值法的实质是根据已知的节点数据或线图上某些已知点的数据构造一个既简单又具有足够精度的插值函数p(x)，并利用该插值函数快速获取原函数在对应位置的数据，这种利用若干节点来构造插值函数的方法称为拉格朗日插值法。

在原函数f(x)上取插值节点数为n+1，分别为(x0，y0)、(x1，y1)、(x2，y2)、…、(xn，yn)，拉格朗日插值多项式的表达式为

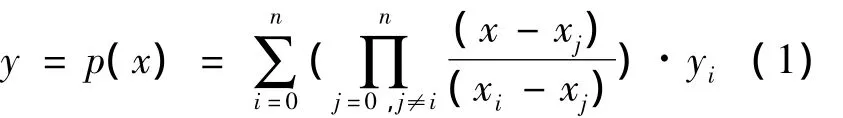
拉格朗日插值法的一个特例就是仅用2个节点(x1，y1)、(x2，y2)来构造插值。由于所表达的函数为线性函数，所以两点插值通常又称为线性插值。线性插值公式构造如下

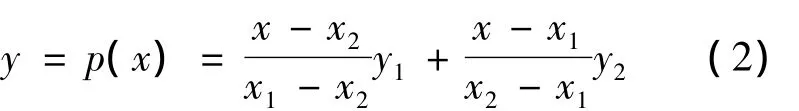
图1为线性插值几何示意图。从图1可以看出，这种插值的结果往往会产生一定的误差。在要求精确数据的某些情况下，这样的误差显然难以满足设计要求。但线性插值公式构造简单，可直接编入程序中计算求值，当节点间隔较小或对节点之间的数据精度无特别要求时，这种插值结果是能满足一般设计要求的。因此在工程设计数据处理过程中，特别是需要查取相邻两点之间数据时大量使用了线性插值。

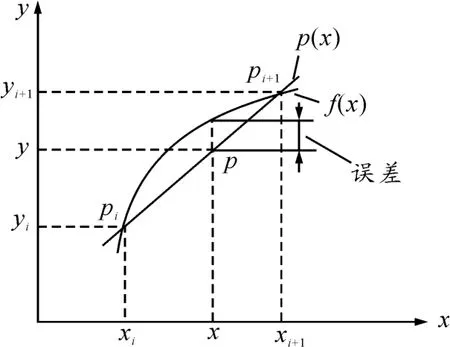
图1 线性插值几何示意图

采用3个插值节点得到的是二次插值多项式，即抛物线插值。相对于线性插值，抛物线插值稍微复杂一些，但插值精度较高，因此在CAD数据处理时应用也很广泛。

抛物线插值最好选取距离插值点最近的个节点以减小插值误差。查找到插值点所在区间后，判断它与前后两点间的距离。如果距离后一点近，则取后面两点与前面一点进行插值(见图2(a);如果距离前一点近，则取前面两点和后面一点进行插值(见图2(b))。

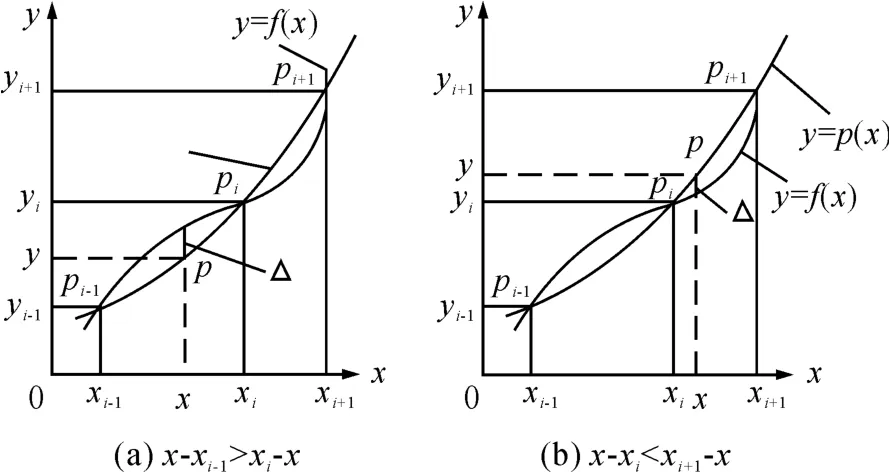
图2 抛物线插值

2 插值法在检索节点区域数据中的应用

2.1 线性插值检索节点区域数据

带传动设计时，需要根据小带轮包角大小来查取包角修正系数Kα，见表1。表1的包角值往往是位数为0和5的整数，如果实际包角值在某2个节点区域内，就必须插值检索。

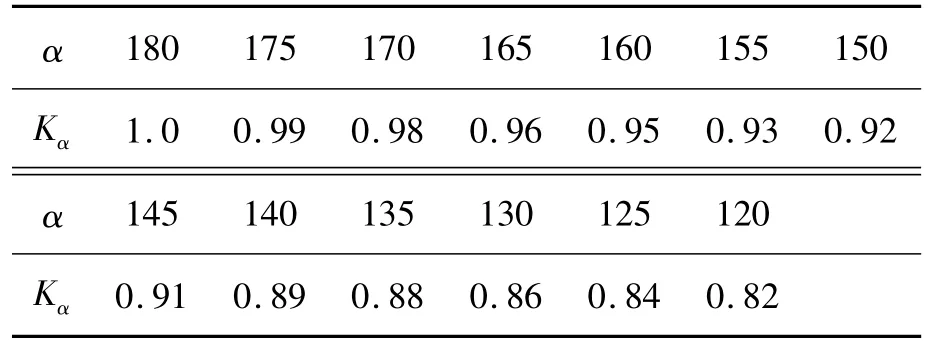
表1 小带轮包角修正系数Kα

利用Auto LISP编程，可将表中节点上的包角和包角系数分别放在2个表变量中，根据给定的实际包角值先检索出左右相邻的节点值，再通过线性插值确定实际的包角修正系数。

包角检索函数定义如下:

(setq ab1(nth i ab)ab2(nth(+i 1)ab)));按条件循环检索出所需数据，再代入公式进行插值计算(setq y1(nth i kab)y2(nth(+i 1)kab))(setq yy(－y2 y1)xx(/(－ab2 bjiao)(－ab2 ab10.0)))(setq ka1(－y2(*yy xx))));输出插值结果

算例1 取小带轮包角α1=148°，执行函数(bjka 148)，得到包角系数 Kα=0.916;若取包角α1=162°，执行函数(bjka 162)，将检索出包角系数 Kα=0.954。

2.2 抛物线插值检索节点区域数据

渐开线齿轮齿根弯曲强度计算时，需要根据齿轮齿数z(zv)查取齿形系数YFa，由于齿数为30以后的数据跨距增大，故可采用抛物线插值检索齿轮齿形系数，见表2。

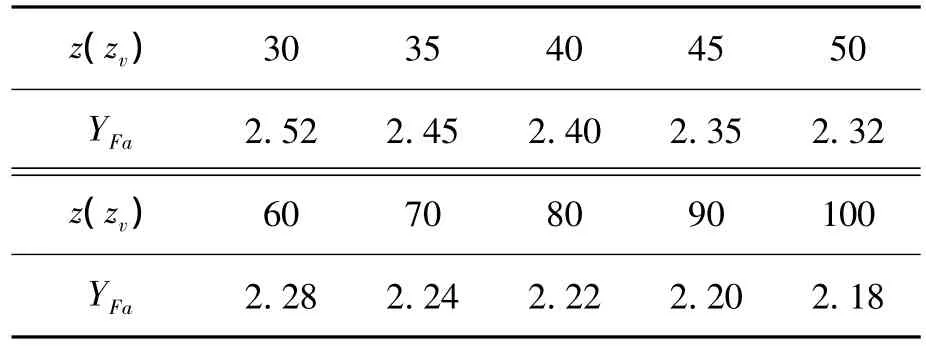
表2 齿形系数YFa

设定抛物线插值自变量x为变参，其取值范围为30～100，将表2中数据写入检索程序中。为了保证两端区间的插值节点数及其检索的有效性，在数据表2个端点各增加1个节点(29，2.53)和(150，2.14)。程序定义如下:

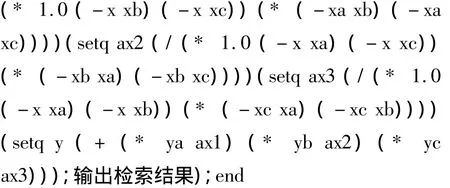
算例2 取齿轮齿数z=57，执行函数(pwxcz 57)，检索得到齿形系数YFa=2.292。在计算机上可以查询到插值节点对应的自变量值为xa=50，xb=60，xc=70，表明插值点更靠近节点(60，2.28)，故以该点及其相邻的两个节点构造了抛物线插值。

如果齿轮齿数z=53，执行函数(pwxcz 53)，将得到齿形系数YFa=2.3052。查询到插值节点为 xa=45，xb=50，xc=60，表明插值点更靠近(50，2.32)，故以该点及其相邻的2个节点构造抛物线插值函数。由此可知，构造抛物线插值的3个插值节点的选取是根据插值点在同一区间(如50～60)自变量与中间节点的距离远近确定的。

3 插值法在检索线图数据中的应用

在工程设计数据中，有很多参数间的关系是用曲线图来表示的。如齿轮动载系数曲线表明了齿轮动载系数与速度和制造精度的关系;动压滑动轴承润滑油流量系数线图(见图3)表明的是润滑油流量系数q/(ψvBd)与相对偏心率χ和轴承宽径比B/d之间的关系。对于这些曲线线图或由曲线表示的数据，通常可用拉格朗日插值来检索。

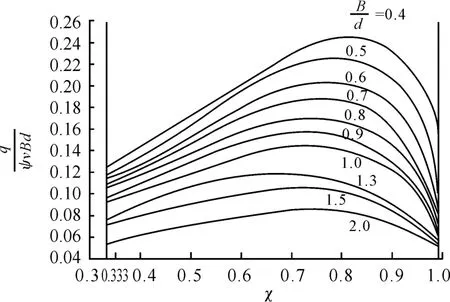
图3 滑动轴承润滑油流量系数

为了构造图3所示曲线的拉格朗日插值函数，可在每一根宽径比对应的曲线上取出若干个点，分别将其节点值赋给表变量xi和yi，然后根据测定的节点个数确定循环次数，进行相应的插值运算，最后输出自变量相对应的函数值。程序定义如下:

算例3 设滑动轴承宽径比B/d=0.6，偏心率 χ=0.713，执行函数(fx 0.7130.6)，得到润滑油流量系数值 Y(x)=0.20131。若取宽径比B/d=0.9，偏心率 χ=0.847，执行函数(fx 0.8470.9)，将得到润滑油流量系数值Y(x)=0.14663。

通过与线图对比，可见检索结果与线图上对应值是完全吻合的。需要说明的是，上述定义的拉格朗日插值函数是一个通用程序，可用于其他类似的线图或数表。函数中表变量xi，yi中的节点数据可以根据具体情况更换。每一条曲线上所取插值节点数可相同，也可不同，节点取多取少基本上没有限制。程序执行时主要由函数(length xi)根据表变量的个数进行循环搜索，并输出检索结果。

4 结束语

随着计算机应用技术的普及，现代设计方法在工程中的应用越来越广泛。高效快捷的设计对工程数据的获取或处理提出了更高的要求。本研究利用AutoLISP中的表变量储存节点数据以及表处理函数的检索功能，将拉格朗日插值法应用于工程CAD中，较好地解决了节点区域数据和曲线线图数据的检索和获取问题，不仅将工程设计人员从重复繁杂的数据查询和设计计算中解放出来，而且大大加快了设计速度。

［1］濮良贵，纪明刚.机械设计［M］.8版.北京:高等教育出版社，2006:291－297.

［2］万小利，高志.计算机辅助机械设计［M］.北京:机械工业出版社，2005:49－55.

［3］林昌华，邢海斌.基于AutoLISP的复杂数据程序化处理［J］.重庆理工大学学报:自然科学版，2012(1):42－46.

［4］林昌华，杨岩.基于递归定义的Auto LISP编程及应用［J］.现代制造工程，2004(12):50 －52.

［5］李志宏.使用AutoLISP程序进行数据文件处理［J］.林业建设，2008(4):61 －62.

［6］李建霞，肖启敏.非图形数据结构在AutoLISP程序进行数据文件处理［J］.煤矿机械，2004(3):62－64.